Quartile Deviation - Measures of Dispersion, Business Mathematics & Statistics | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
QUARTILE DEVIATION
Quartiles are such values which divide the total number of observations into 4 equal parts. Obviously, there are 3 quartiles—
(i) First quartile (or Lower quartile): Q1
(ii) Second quartile, (or Middle quartile) : Q2
(iii) Third quartile (or Upper quartile): Q3
The number of observations smaller than Q1 , is the same as the number lying between Q1 and Q2, or between Q2 and Q3, or larger than Q3. For data of continuous type, one-quarter of the observations is smaller than Q1, two-quarters are smaller than Q2 , and three-quarters are smaller than Q3. This means that Q1, Q2, Q3 are values of the variable corresponding to ‘less-than’ cumulative frequencies N/4, 2N/4, 3N/ 4 respectively. Since, 2N/4 = N/2, it is evident that the second quartile Q2 is the same as median.
Q1 < Q2 < Q3 ; Q2 = Median.
Quartiles are used for measuring central tendency, dispersion and skewness. For instance, the second quartile Q2 is itself taken as a measure of central tendency, where it is known as Median. Quartile deviation is defined as half the difference between the upper and the lower quartiles.
The difference Q3- Q1 being the distance between the quartiles can also be called inter quartile range; half of this Semi- inter quartile Range. Thus the name ‘Semi - inter quartile Range’ itself gives the definition of Quartile Deviation.
Quartile Deviation (Q.D.) is dependent on the two quartiles and does not take into account the variability of the largest 25% or the smallest 25% of observations. It is therefore unaffected by extreme values. Since in most cases the central 50% of observation tend to be fairly typical, Q.D. affords a convenient measure of dispersion. It can be calculated from frequency distributions with open-end classes. Q.D. is thus superior to Range in many ways. Its unpopularity lies in the fact that Q.D. does not depend on the magnitudes of all observations. The calculation of Q.D. only depends on that of the two quartiles, Q1 and Q3 which can be found from a cumulative frequency distribution using simple interpolation.
Example and Solution.
Example 1. Calculate the quartile deviation from the following:
Solution. In order to compute Quartile Deviation, we have to find QI and Q3 i.e. values of the variable corresponding to Cumulative frequencies N/4 and 3N/4. Here, total frequency N = 82. Therefore, N/4 = 20.5 and 3N/4 = 61.5
Example 2. Calculate the appropriate measure of dispersion from the following data :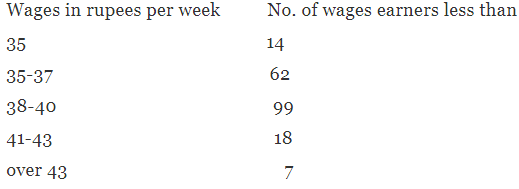
Solution. Since there are open-end classes in the frequency distribution. Quartile deviation would be the most appropriate measure of dispersion for the data. So, we have to determine the quartiles QI and Q3 which can be done from cumulative frequency distribution using simple interpolation.
Applying Simple interpolation,
Example 3. Consider the following scores of 10 CFA Level 1 candidates
78 56 67 51 43 89 57 67 78 50
Solution. Range = 89 – 43 = 46
Example 4. 6 Investment analysts attain the following returns on six different investments:
{12% 4% 23% 8% 9% 16%}
Calculate the mean absolute deviation and interpret it.
Solution. First, we have to calculate the arithmetic mean: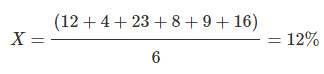
Next, we can now compute the MAD: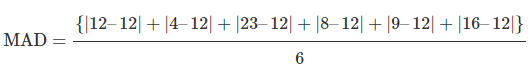
= 30/6
= 5%
Interpretation: It means that on average, an individual return deviates 5% from the mean return of 12%
Example 5. Working with data from example 2 above, the variance will be calculated as follows:
Solution.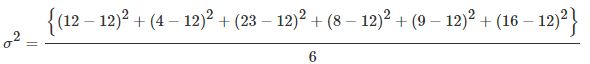
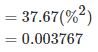
Thus, the average variation from the mean (0.12) is 0.003767.
The standard deviation is 0.0037671/2 = 0.06137 or 6.14%
Analysts use the standard deviation to interpret returns as opposed to the variance since it is much easier to comprehend.
Example 6. Assume that the returns realized in example 2 above were sampled from a population comprising 100 returns. Compute the sample mean and the corresponding sample variance.
Solution. The sample mean will still be 12%
Hence,
Therefore,
|
1334 videos|1437 docs|834 tests
|
FAQs on Quartile Deviation - Measures of Dispersion, Business Mathematics & Statistics - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year
| 1. What is quartile deviation and how is it calculated? |  |
| 2. How is quartile deviation different from range and standard deviation? |  |
| 3. Can quartile deviation be negative? |  |
| 4. What does a high quartile deviation indicate? |  |
| 5. How is quartile deviation useful in business statistics? |  |






















