Ex-10.1, Basic Geometrical Concepts, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
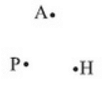
Question 1. Make three points in your notebook and name them.
Solution : Three points, namely A,P and H can be marked as follows
Question 2. Draw a line in your notebook and name it using a small letter of the alphabet
Solution : Let us draw a line and name it l

Question 3. Draw a line in your notebook and name it by using two points on it
Solution : Let us first draw a line. Two points on it are P and Q. now, the line can be written as line PQ

Question 4. Give three examples from your environment of:
i) Points
ii) Portion of a line
iii) Plane of the surface
iv)Portion of the line
v) Curved surface
Answer:
i) The period at the end of the sentence, a pinhole on the map and the point at which two walls and the floor meet at the corner of the room.
ii) Tightly stretched power cables, laser beams, and thin curtain rods
iii) The surface of a smooth wall, the surface of the top of a table and the surface of a smooth white board
iv) The surface of the sheet of the paper, the surface of calm water in a swimming pool and the surface of a mirror
v) The surface of a gas cylinder, the surface of a tea pot and the surface of an ink pot .
Question 5. There are a number of ways by which we can visualize a portion of a line. State whether the following represent a portion of line or not:
i) A piece of elastic stretched to the breaking point
ii) Wire between two electric poles
iii) The line thread by which a spider lowers itself
Answer:
i) Yes
ii) No
iii) Yes
Question 6. Can you draw a line on the surface of a sphere which lies wholly on it?
Solution : No, we cannot draw a line on the surface of the sphere, which lies wholly on it.
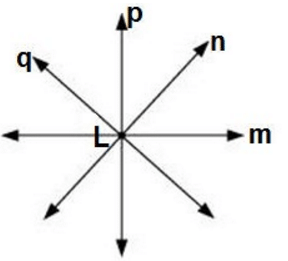
Questions 7. Make appoint on the sheet of a paper and draw a line passing through it. How many lines can you draw through this point?
Solution : Unlimited number of lines can be drawn passing through a point L
Question 8. Mark any two points P and Q in your notebook and draw a line passing through the points.
How many lines can you draw passing through this both points?
Solution : We have two points P and Q and we draw a line passing through these two points.
Only one line can be drawn passing through these two points.

Question 9. Give an example of the horizontal plane and a vertical plane from your environment.
Solution : Ceiling of a room is an example of a horizontal plane in our environment.
Wall of a room is an example of a vertical plane in our environment.
Question 10. How many lines may pass through one given point , two given point , any three collinear points?
Solution : Lines passing through one point – unlimited
Lines passing through two points – one

Lines passing through any three collinear points – one
Question 11. Is it ever possible for exactly one line to pass through three points?
Solution : Yes, it is possible if three points lie on a straight line
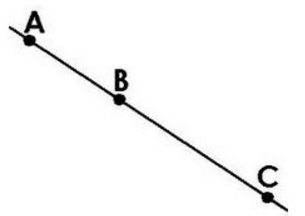
Question 12. Explain why is not possible for a line to have a mid point?
Solution : The length of the line is infinite. Thus, it is not possible to find its midpoint. On the other hand, we can find, we can find the midpoint of a line segment
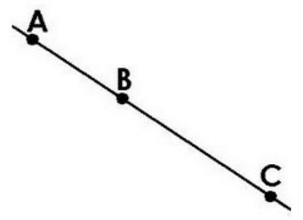
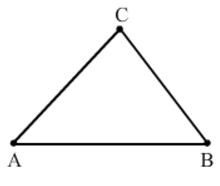
Question 13. Mark three non – collinear points points A,B,C in your notebook . Draw the lines through the points taking two at a time. Name these lines. How many such different lines can be drawn ?
Solution : These are three non – collinear points A,B,C
Three lines can be drawn through these points. These three lines are AB, BC and AC
Question 14. Coplanar points points are the points that are in the same plane. Thus,
i) Can 150 points be coplanar?
Answer: Yes,
A group of points that lie in the same plane are called co planar points.
Thus, it is possible that 150 points can be co-planar.
ii) Can 3 points be non – co planar?
Answer: No
3 points will be coplanar because we can have a plane that can contain 3 points on it.
Thus, it is not possible that 3 points will be non – coplanar.
Question 15. Using a ruler, check whether the following points given in the figure are collinear or not?

Answer:
i) D,A and C are collinear points
ii)A,B and C are non – collinear points
iii) A,B and E are collinear points
iv) B,C and E are non – collinear points
Question 16. Lines p, q is coplanar. So are the lines p, r. Can we conclude that the lines p, q, r are coplanar?
Solution : No, p,q and r are not necessarily coplanar.
Example – if we take p as intersecting line of two consecutive walls of a room , q as a line on the first wall and r on the second wall whose (both walls) intersection is line p
Thus we can see that p,q and r are not coplanar.
Question 17. Give three examples of each:
i) Intersecting lines :
Answer:
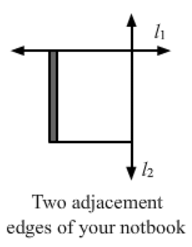
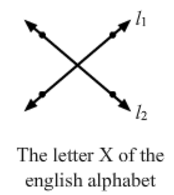
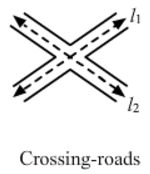
i) Parallel lines from your environment:
Answer:
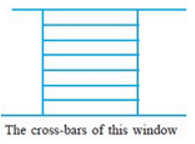

Question 18. From the figure write:

Answer:
i) All pairs of intersecting lines
Answer: (l,m) ,(m,n) , and (l,n)
ii) All pairs of intersecting lines
Answer: (l,p) , (m,p) , ( n,p) , (l,r) , (m,r) , (n,r) ,(I,q),(m,q),(n,q) , (q,p) ,(q,r)
iii) Lines whose point of intersection is l
Answer: (m,p)
iv) Lines whose point of intersection is D
Answer: (l,r)
v) Lines whose point of intersection E
Answer: (m,r)
vi) Lines whose point of intersection is A
Answer: ( l,q)
vii) Collinear points
Answer: (G,A,B and C) ,(D,E,J and F) , ( G,H,I and J,K) ,(A,H,and D) ,(B,I and E) and ( C,F and K)
Question 19. Write concurrent lines and their and their point of concurrence:
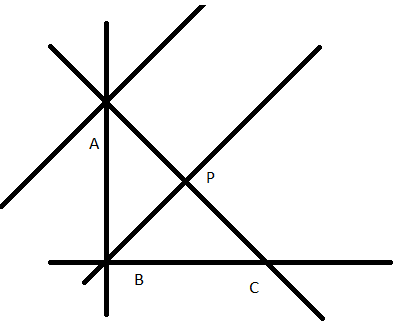
Answer:
From the given figure, we have :
Concurrent lines can be defined as three or more lines which share the same meeting point. Clearly lines, n,q, and l are concurrent with A as the point of concurrence .
Lines, m,q and p are concurrent with B as the point of concurrence.
Question 20. Mark four points A,B,C,D in your notebook such that no three of them are collinear . Draw all the lines which join them in pairs as shown
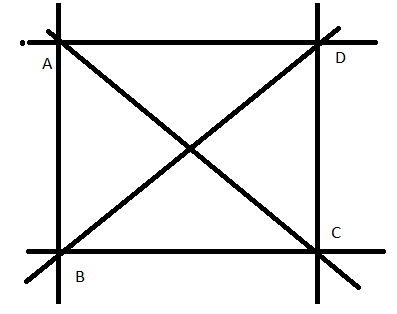
i) How many such lines can be drawn
Answer: Six lines can be drawn through these four points as given in the figure.
ii) Write the names of these lines
Answer: These lines are AB, BC, CD, BD and AD
iii) Name the lines which are concurrent to A
Answer: Lines which are concurrent at A are AC, AB and AD
Question 21. What is the maximum number of points of intersection of three lines in a plane? What is the minimum number?
Solution : Maximum number of points of intersection of three lines in a plane will be three
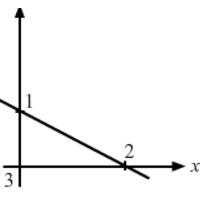
Minimum number of points of intersection of three lines in a plane will be zero
Question 22. With the help of a figure, find the maximum and minimum number of points of intersection of four lines in a plane.
Solution : Maximum number of points of intersection of four lines in a plane will be six
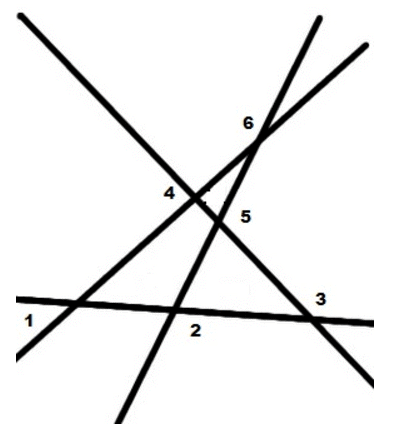
Minimum number of points of intersection of four lines in a plane will be zero.

Question 23. Lines p,q and r are concurrent. Also, the lines p, r and s are concurrent. Draw a figure and state whether lines p,q, r and s are concurrent or not?
Solution : 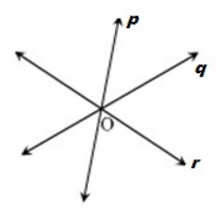
Thus, lines p,q and r intersect at a common point O
Also, lines p,r, and s are concurrent
Therefore, lines p, r, and s intersect at a common point. But q and r intersect each other at O.
So, p,q and r intersect at O
Hence, p,q,r and s are concurrent . Lines p, q,r and s intersect at O
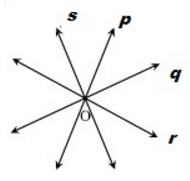
Question 24. Lines p, q, and r are concurrent. Also lines p,s and t are concurrent . Is it always true that the lines q,r and s will be concurrent? Is it always true for lines q, r, and t?
Solution : Lines p, q, and r are concurrent. So, lines p, q and r intersect at a common point O
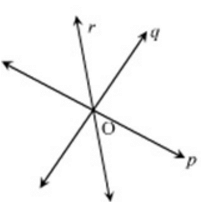
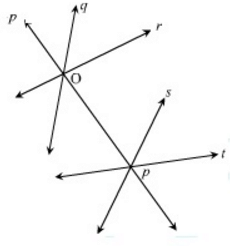
Given lines p, s, and t are concurrent. So, lines p, s and t also intersect at a common point. However, it is not always true that q, r and s or q, r and t are concurrent.
Question 25. Fill in the blanks in the following statements using suitable words:
i) A page of a book is a physical example of a
Answer: plane
ii) An inkpot has both ____________ surfaces
Answer: curved and plane
iii) Two lines in a plane are either______or are_______
Answer: parallel or are intersecting
Question 26. State which of the following statements are true and which are false:
i) Point has a size because we can see it as a thick dot on paper – False
ii) By lines in geometry , we mean only straight lines – True
iii) Two lines in a plane always intersect at a point – False
iv) Any plane through a vertical line is vertical – True
v) Any plane through a horizontal line is horizontal – False
vi) There cannot be a horizontal line in a vertical plane – False
vii) All lines in a horizontal plane are horizontal – True
viii) Two lines in a plane always intersect at a plane – False
ix) If two lines intersect at a point P , then P is called the point of concurrence of the two lines – False
x) If two lines intersect at a point P , then P is called the point of intersection of the two lines- True
xi) If A,B,C and D are collinear points D,P and Q are collinear , then points A,B,C,D,P and Q are always collinear – False
xii) Two different lines can be drawn passing through two given points – False
xiii) Through a given point only one line can be drawn – False
xiv) Four points are collinear if any three of them lie on them lie on the same line – False
xv)The maximum number of points of intersection of three lines is three – True
xvi)The minimum number of points of intersection of three lines is one – False
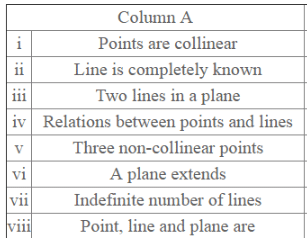
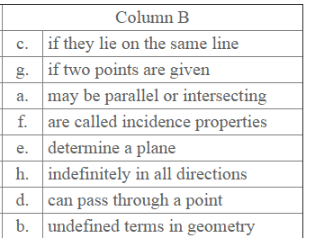
Question 27. Give the correct matching of the statements of column A and column B
FAQs on Ex-10.1, Basic Geometrical Concepts, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. What are the basic geometrical concepts covered in Class 6 Maths? |  |
| 2. How can I understand the basic geometrical concepts better? |  |
| 3. How are points, lines, and line segments different from each other? |  |
| 4. What are the properties of triangles and quadrilaterals? |  |
| 5. How can I measure angles and circles accurately? |  |

|
Explore Courses for Class 6 exam
|

|


















