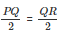Ex-10.1, Congruent Triangles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
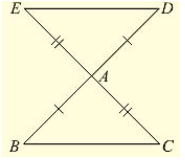
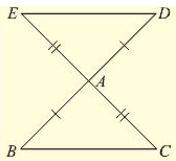
(1) In Fig. (10).22, the sides BA and CA have been produced such that: BA = AD and CA = AE. Prove that segment DE ∥ BC.
Solution:
Given that, the sides BA and CA have been produced such that BA = AD and CA = AE and given to prove DE ∥ BC Consider triangle BAC and DAE,
We have
BA = AD and CA= AE [given in the data]
And also ∠BAC = ∠DAE [vertically opposite angles]
So, by SAS congruence criterion, we have
∠BAC ≃ ∠DAE
- BC = DE and ∠DEA = ∠BCA, ∠EDA = ∠CBA
[Corresponding parts of congruent triangles are equal]
Now, DE and BC are two lines intersected by a transversal DB such that ∠DEA = ∠BCA i.e.. alternate angles are equal Therefore, DE BC ∥ BC.
Q. (2) In a PQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN = MN.
Solution: Given that,
In PQR, PQ = QR and L, M, N are midpoints of the sides PQ, QP and RP respectively and given to prove that LN = MN
Here we can observe that PQR is an isosceles triangle
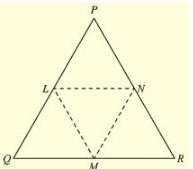
- PQ = QR and ∠ QPR = ∠ QRP _____(i)
And also, L and M are midpoints of PQ and QR respectively
- PL = LQ = QM = MR =

And also, PQ = QR
Now, consider Δ LPN and Δ MRN, LP = MR [From – (2)]
∠ LPN = ∠ MRN __ [From – (1)]
∠ QPR and ∠ LPN and ∠ QRP and ∠ MRN are same.
PN = NR [N is midpoint of PR]
So, by SAS congruence criterion, we have Δ LPN = Δ MRN
- LN = MN [Corresponding parts of congruent triangles are equal]
Q. (3) In fig. (10).23, PQRS is a square and SRT is an equilateral triangle. Prove that (i) PT = QT (ii) ∠ TQR = 15∘
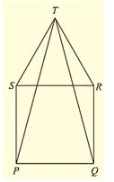
Solution: Given that PQRS is a square and SRT is an equilateral triangle. And given to prove that
(i) PT =QT and (ii) ∠ TQR =15°
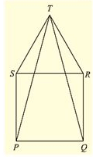
Now, PQRS is a square
- PQ = QR = RS = SP ____(i)
- And ∠ SPQ = ∠ PQR = ∠ QRS = ∠ RSP = 90∘ = right angle
And also, SRT is an equilateral triangle.
- SR = RT = TS ___(ii)
And ∠ TSR = ∠ SRT = ∠ RTS = 60°
From (i) and (ii)
PQ = QR = SP = SR = RT = TS ___(iii)
And also,
∠ TSP = ∠ TSR + ∠ RSP = 60° + 90° + 150°
∠TRQ = ∠TRS + ∠ SRQ = 60° + 90° + 150°
⇒ ∠ TSR = ∠ TRQ = 150∘ ____ (iv)
SP = RQ [From (iii)]
So, by SAS congruence criterion we have
Δ TSP = Δ TRQ
PT = QT [Corresponding parts of congruent triangles are equal] Consider Δ TQR.
QR = TR [From (iii)]
Δ TQR is a isosceles triangle.
∠ QTR = ∠ TQR [angles opposite to equal sides]
Now,
Sum of angles in a triangle is equal to 180∘
⇒ ∠ QTR + ∠ TQR + ∠TRQ = 180°
⇒ 2 ∠ TQR + 150° = 180° [From (iv)]
⇒ 2 ∠ TQR = 180° – 150°
⇒ 2 ∠ TQR = 30° ∠ TQR = 15°]…
Hence proved
Q. (4) Prove that the medians of an equilateral triangle are equal.
Solution:
Given,
To prove the medians of an equilateral triangle are equal.
Median: The line Joining the vertex and midpoint of opposite side. Now, consider an equilateral triangle ABC.
Let D,E,F are midpoints of BC, CA and AB.
Then, AD, BE and CF are medians of ABC.
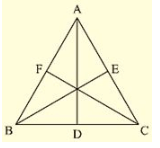
Now,
D Is midpoint of BC ⇒ BD = DC =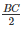
Similarly, CE = EA = 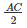
AF = FB = 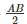
Since Δ ABC is an equilateral triangle
⇒ AB = BC = CA _____(i)
⇒ BD = DC = CE = EA = AF = FB = 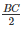 =
= 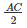 =
= 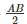 _____(ii)
_____(ii)
And also, ∠ ABC = ∠ BCA = ∠ CAB = 60° _____(iii)
Now, consider Δ ABD and Δ BCE AB = BC [From (i)]
BD = CE [From (ii)]
Now, in Δ TSR and Δ TRQ
TS = TR [From (iii)]
∠ ABD = ∠ BCE [From (iii)] [∠ ABD and ∠ ABC and ∠ BCE and ∠BCA are same]
So, from SAS congruence criterion, we have
Δ ABD = Δ BCE
AD = BE ____(iv)
[Corresponding parts of congruent triangles are equal]
Now, consider Δ BCE and Δ CAF, BC = CA [From (i)]
∠ BCE = ∠ CAF [From (ii)]
[∠ BCE and ∠ BCA and ∠ CAF and ∠ CAB are same]
CE = AF [From (ii)]
So, from SAS congruence criterion, we have
Δ BCE = Δ CAF
- BE = CF (v)
[Corresponding parts of congruent triangles are equal]
From (iv) and (v), we have
AD = BE = CF
- Median AD = Median BE = Median CF
The medians of an equilateral triangle are equal.
Hence proved
Q. (5) In a Δ ABC, if ∠ A = 120° and AB = AC. Find ∠ B and ∠ C.
Solution:
Consider a Δ ABC
Given Mat ∠ A = 120° and AB = AC and given to find ∠ B and ∠ C.
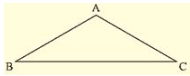
We can observe that Δ ABC is an isosceles triangle since AB = AC
- ∠ B = ∠ C (i)
[Angles opposite to equal sides are equal]
We know that sum of angles in a triangle is equal to 180°
⇒ ∠ A + ∠ B + ∠ C= 180° [From (i)]
⇒ ∠ A + ∠ B + ∠ B= 180°
⇒ 120∘ + 2∠B = 180∘
⇒ 2∠B = 180∘ – 120∘
⇒ ∠ B = ∠ C = 30∘
Q. (6) In a Δ ABC, if AB = AC and ∠ B = 70°. Find ∠ A.
Solution:
Consider a Δ ABC, if AB = AC and ∠ B = 70°
Since, AB = AC Δ ABC is an isosceles triangle
- ∠ B = ∠ C [Angles opposite to equal sides are equal]
- ∠ B = ∠ C = 70∘
And also,
Sum of angles in a triangle = 180∘
- ∠ A + ∠ B +∠ C = 180∘
- ∠ A + 70∘ + 70∘ = 180∘
- ∠ A = 180∘ – 140∘
- ∠ A = 40∘
Q. (7) The vertical angle of an isosceles triangle is (10)0∘. Find its base angles.
Solution:
Consider an isosceles ΔABC such that AB = AC
Given that vertical angle A is (10)0∘
To find the base angles
Since Δ ABC is isosceles
- ∠ B = ∠ C [Angles opposite to equal sides are equal]
And also,
Sum of interior angles of a triangle = 180∘
- ∠ A + ∠ B +∠ C = 180∘
- (10)0∘ + ∠ B ∠ B = 180∘
- 2∠ B = 180∘ – (10)0∘
- ∠ B = 40∘
- ∠ B = ∠ C = 40∘
Q. (8) In Fig. (10).24, AB = AC and ∠ ACD = (10)5∘. Find ∠ BAC.
Solution:
Consider the given figure
We have,
AB = AC and ∠ ACD = (10)5∘
Since, ∠ BCD = 180° = Straight angle
- ∠ BCA + ∠ ACD =180°
- ∠ BCA + (10)5° = 180°
- ∠ BCA = l80° -(10)5°
- ∠BCA= 75°
And also,
ΔABC is an isosceles triangle [AB = AC]
- ∠ ABC = ∠ ACB [Angles opposite to equal sides are equal]
From (i), we have
∠ ACB = 75°
- ∠ ABC = ∠ ACB = 75°
And also,
Sum of Interior angles of a triangle = 180 ∘
- ∠ ABC = ∠ BCA + ∠ CAB =180°
- 75° + 75° + ∠ CAB =180°
- 150° + ∠ BAC = 180°
- ∠ BAC = 180° -150° = 30°
- ∠ BAC = 30°
Q. (9) Find the measure of each exterior angle of an equilateral triangle.
Solution:
Given to find the measure of each exterior angle of an equilateral triangle consider an equilateral triangle ABC.
We know that for an equilateral triangle
AB = BC = CA and ∠ ABC = ∠ BCA= CAB =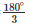 = 60° ____(i)
= 60° ____(i)
Now,
Extend side BC to D, CA to E and AB to F.
Here BCD is a straight line segment
- BCD = Straight angle =180°
- ∠ BCA + ∠ ACD = 180° [From (i)]
- 60° + ∠ACD = 180°
- ∠ACD = 120°
Similarly, we can find ∠ FAB and ∠ FBC also as 120° because ABC is an equilateral triangle
∠ ACD = ∠ EAB – ∠ FBC = 120°
Hence, the median of each exterior angle of an equilateral triangle is 120°
Q. (10) If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Solution:
ED is a straight line segment and B and C an points on it.
- ∠ EBC = ∠ BCD = straight angle = 180°
- ∠ EBA+ ∠ ABC = ∠ ACB + ∠ ACD
- ∠ EBA = ∠ ACD + ∠ ACB – ∠ ABC
- ∠ EBA = ∠ ACD [From (i) ABC = ACD]
∠ ABE = ∠ ACD
Hence proved
Q. (11) In Fig. (10).2(5) AB = AC and DB = DC, find the ratio ∠ ABD : ∠ ACD.
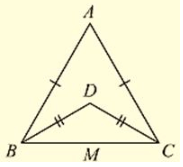
Solution:
Consider the figure
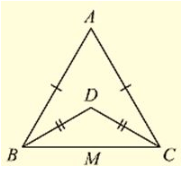
Given,
AB = AC, DB = DC and given to find the ratio
∠ ABD = ∠ ACD
Now, Δ ABC and Δ DBC are isosceles triangles since AB = AC and DB = DC respectively
- ∠ ABC = ∠ ACB and ∠ DBC = ∠ DCB [Angles opposite to equal sides are equal]
Now consider,
∠ ABD : ∠ ACD
- (∠ ABC – ∠ DBC) : (∠ ACB – ∠ DCB)
- (∠ ABC – ∠ DBC) : (∠ ABC – ∠ DBC) [∠ ABC = ∠ ACB and ∠ DBC = ∠ DCB]
- 1:1
ABD: ACD = 1:1
Q. (12) Determine the measure of each of the equal angles of a right-angled isosceles triangle.
OR
ABC is a right-angled triangle in which ∠ A = 90° and AB = AC. Find ∠ B and ∠ C.
Solution:
ABC is a right angled triangle
Consider on a right – angled isosceles triangle ABC such that
∠ A = 90∘ and AB = AC Since,
AB = AC ⇒ ∠ C = ∠ B ____(i)
[Angles opposite to equal sides are equal]
Now, Sum of angles in a triangle = 180 ∘
∠ A + ∠ B + ∠ C =180°
⇒ 90° + ∠ B+ ∠ B = 180°
⇒ 2∠ B = 90°
⇒ ∠ B = 45°
∠ B = 45°, ∠ C = 45°
Hence, the measure of each of the equal angles of a right-angled Isosceles triangle Is 45°
Q. (13) AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. (10).26). Show that the line PQ is perpendicular bisector of AB.
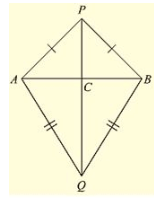
Solution:
Consider the figure.
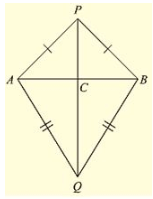
We have
AB is a line segment and P, Q are points on opposite sides of AB such that
AP = BP __________(i)
AQ = BQ ___________(ii)
We have to prove that PQ is perpendicular bisector of AB.
Now consider Δ PAQ and Δ PBQ,
We have
AP = BP [From (i)]
AQ = BQ [From (ii)]
And PQ – PQ [Common site]
Δ PAQ ≃ Δ PBQ ______(iii) [From SAS congruence]
Now, we can observe that APB and ABQ are isosceles triangles. [From (i) and (ii)]
- ∠ PAB = ∠ ABQ and ∠ QAB = ∠ QBA
Now consider Δ PAC and Δ PBC
C is the point of intersection of AB and PQ
PA = PB [From (i)]
∠ APC = ∠ BPC [From (ii)]
PC = PC [common side]
So, from SAS congruency of triangle ΔPAC≅ΔPBC
- AC = CB and ∠ PCA = ∠ PBC _________(iv) [ Corresponding parts of congruent triangles are equal]
And also, ACB is line segment - ∠ ACP + ∠ BCP = 180 ∘
- ∠ ACP = ∠ PCB
- ∠ ACP = ∠ PCB = 90∘<
We have AC = CB ⇒ C is the midpoint of AB
From (iv) and (v)
We can conclude that PC is the perpendicular bisector of AB
Since C is a point on the line PQ, we can say that PQ is the perpendicular bisector of AB.
FAQs on Ex-10.1, Congruent Triangles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What are congruent triangles? |  |
| 2. How can I prove that two triangles are congruent? |  |
| 3. How many congruent triangles can be formed if two sides and an angle of one triangle are given? |  |
| 4. Can two triangles with all sides equal be congruent? |  |
| 5. Are congruent triangles similar as well? |  |

|
Explore Courses for Class 9 exam
|

|