Ex-10.2, Congruent Triangles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q. (1) In fig. (10).40, it is given that RT = TS, ∠ 1 = 2 ∠ 2 and 4 = 2 ∠ (3) Prove that ΔRBT ≅ ΔSAT.
Solution:
In the figure, given that
RT = TS ……(i)
∠ 1 = 2 ∠ 2 ……(ii)
And ∠ 4 = 2 ∠ 3 ……(iii)
To prove that ΔRBT ≅ ΔSAT.
Let the point of intersection RB and SA be denoted by O
Since RB and SA intersect at O
∠ AOR = ∠ BOS [Vertically opposite angles]
- ∠ 1 = ∠ 4
- 2 ∠ 2 = 2 ∠ 3 [From (ii) and (iii)]
- ∠ 2 = ∠ 3 ……(iv)
Now we have RT =TS in Δ TRS
Δ TRS is an isosceles triangle
∠ TRS = ∠ TSR ……(v)
But we have
∠ TRS = ∠ TRB + ∠ 2 ……(vi)
∠ TSR = ∠ TSA + ∠ 3 ……(vii)
Putting (vi) and (vii) in (v) we get
∠ TRB + ∠ 2 = ∠ TSA + ∠ B
=> ∠ TRB = ∠ TSA [From (iv)]
Now consider Δ RBT and Δ SAT
RT = ST [From (i)]
∠ TRB = ∠ TSA [From (iv)] ∠ RTB = ∠ STA [Common angle]
From ASA criterion of congruence, we have
Δ RBT = Δ SAT
Q. (2) Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Solution: Given that lines AB and CD Intersect at O
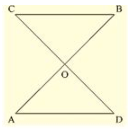
Such that BC ∥ AD and BC = AD …….(i)
We have to prove that AB and CD bisect at O.
To prove this first we have to prove that Δ AOD ≅ Δ BOC
Q. (3) BD and CE are bisectors of ∠ B and ∠ C of an isosceles Δ ABC with AB = AC. Prove that BD = CE
Solution:
Given that Δ ABC is isosceles with AB = AC and BD and CE are bisectors of ∠ B and ∠ C We have to prove BD = CE
Since AB = AC
=> Δ ABC = Δ ACB ……(i)
[Angles opposite to equal sides are equal]
Since BD and CE are bisectors of ∠ B and ∠ C
- ∠ ABD = ∠ DBC = ∠ BCE = ECA =
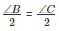
Now,
Consider Δ EBC = Δ DCB
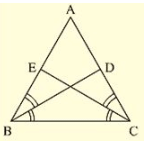
∠ EBC = ∠ DCB [∠ B = ∠ C] [From (i)]
BC = BC [Common side]
∠ BCE = ∠ CBD [From (ii)]
So, by ASA congruence criterion, we have Δ EBC ≅ Δ DCB
Now,
CE = BD [Corresponding parts of congruent triangles we equal]
or, BD = CE
Hence proved
Since AD ∥ BC and transversal AB cuts at A and B respectively
∠ DAO = ∠ OBC …….(ii) [alternate angle]
And similarly AD ∥ BC and transversal DC cuts at D and C respectively
∠ ADO = ∠ OBC ..…(iii) [alternate angle]
Since AB end CD intersect at O.
∠ AOD = ∠ BOC [Vertically opposite angles]
Now consider Δ AOD and Δ BOD
∠ DAO = ∠ OBC [From (ii)]
AD = BC [From (i)]
And ∠ ADO = ∠ OCB [From (iii)]
So, by ASA congruence criterion, we have
ΔAOD≅ΔBOC
Now,
AO= OB and DO = OC [Corresponding parts of congruent triangles are equal)
- Lines AB and CD bisect at O.
Hence proved
FAQs on Ex-10.2, Congruent Triangles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What are congruent triangles? |  |
| 2. How can we prove two triangles are congruent? |  |
| 3. What is the importance of congruent triangles? |  |
| 4. How do congruent triangles help in solving real-life problems? |  |
| 5. Can two triangles be congruent if they have different angles? |  |
















