Ex-15.1 & 15.2, Pair Of Lines And Transversal, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
Question 1. Identify parallel line segments:
i)
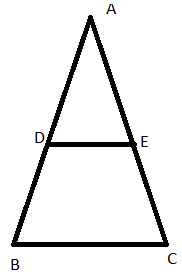
ii)

iii)
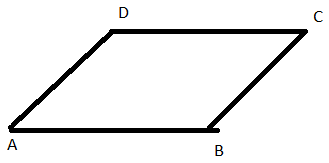
iv)
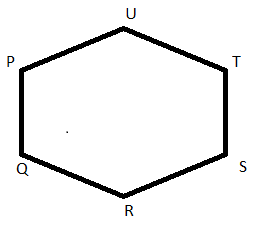
v)
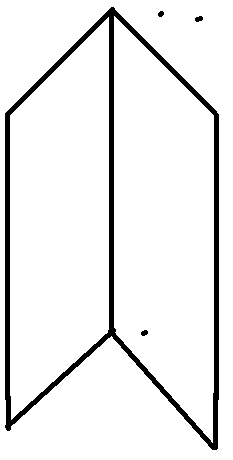
vi)
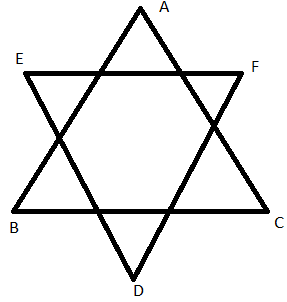
Answer:
- BC ║ DE
- AB ║ DC , AD ║ BC
- AB ║ DC , AD ║ BC
- PQ ║ TS , UT ║QR , UP ║ SR
- AB ║ DC ║ EF , AD ║ BC and DE║ CF
- BC ║ EF , AB ║ DF and AC ║ DE
Question 2. Name the pairs of all possible parallel edges of the pencil box whose figure is shown in the figure
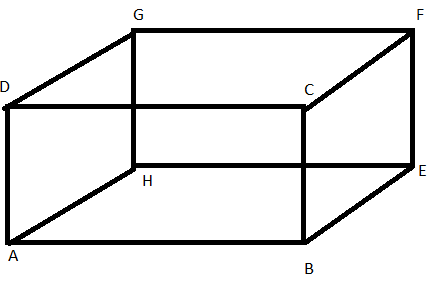
Answer:
AH║DG║CF║BE
AB║DC?GF║HE
AD║HG║EF║BC
Question 3. In the figure, do the segments AB and CD intersect ? are they parallel? Give reasons.
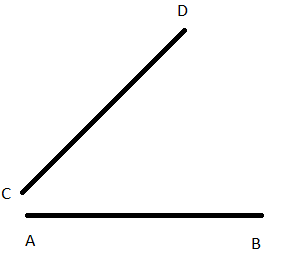
Answer:
In the given position , segments AB and CD do not intersect , but hey can if extended to a point . No, they are not parallel, as the dstance between them is not constant.
Question 4. State which of the following are true or false:
i) If two lines in the same plane do not intersect , then they must be parallel
Ans. True
ii) Distance between two parallel lines is not same everywhere
Ans. False
iii) If m perpendicular l and n perpendicular l and m ? n , then m parallel to n
Ans. True
iv) Two non Ans. intersecting co Ans.planar rays are parallel
Ans. False
iv) If Ray AB parallel to m , then line segment AB parallel to m
Ans. True
v) If Ray AB parallel to m , then line segment AB parallel to m
Ans. True
vi) No two parallel segments intersect each other
Ans. True
vii) Every pair of lines is a pair of co-planar lines
Ans. False
viii) Two lines perpendicular to the same line are parallel
Ans. True
ix) A line perpendicular to one of two parallel lines is perpendicular to each other
Ans. True
Exercise 15.2
Question 1. i) Alternate corresponding angles
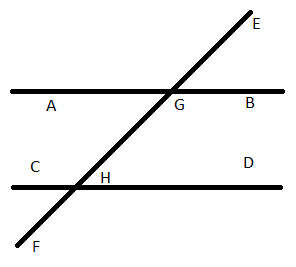
Answer:
Alternate interior angles are:
Angle BGH and angle CHG
Angle AGH and angle CHF
Alternate exterior angles:
Angle AGE and angle DHF
Angle EGB and angle CHF
Corresponding angles are:
Angle EGB and angle GHD
Angle EGA and angle GHC
Angle BGH and angle DHF
Angle AGF and angle CHF
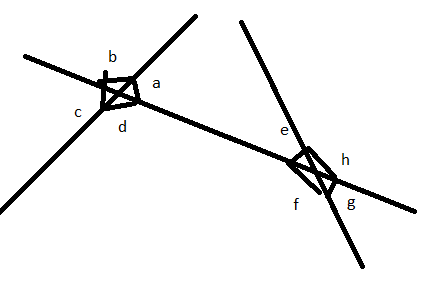
ii) Angles alternate to ∠d and ∠g and angles corresponding to angles ∠f and ∠h in the figure
Answer:
The alternate angle to ∠d is ∠e and alternate angles to ∠g is ∠b
The corresponding angles to ∠f is ∠c and ∠h is ∠a
iii) Angles alternative to ∠PQR , angle corresponding to ∠RQF and angle alternative to ∠PQE in the figure
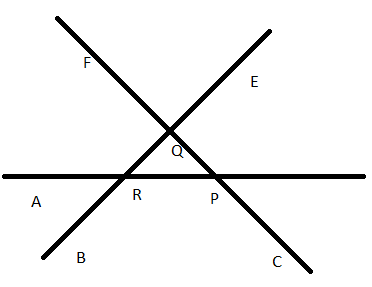
In the given figure. ‘I’ is a transversal to ‘m’ and ‘n’
So, the alternate angle of ∠PQR is ∠QRA
The corresponding angle ∠RQF and ∠BRA
The alternate angle of ∠PQE is ∠BRA
iv) Interior angles on the same side of the transversal line ‘n’ are ∠d and ∠f , ∠a and ∠e
Exterior angles on the same side of the transversal line ‘n’ are ∠c and ∠g , ∠b and ∠h
Question 2. Match column A and column B .
i) Vertically opposite angles - c - ∠PAB and ∠XAQ
ii) Alternate angles - a - ∠PAB and ∠ABS
iii) Corresponding angles – b - ∠PAB and ∠RBY
FAQs on Ex-15.1 & 15.2, Pair Of Lines And Transversal, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. What are the different types of pairs of lines? |  |
| 2. How do you identify intersecting lines? |  |
| 3. How can you determine if two lines are parallel? |  |
| 4. What are coincident lines? |  |
| 5. How does a transversal intersect a pair of lines? |  |

|
Explore Courses for Class 6 exam
|

|

















