Ex-15.2, Areas Of Parallelograms And Triangles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1. If figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm, and CF = 10 cm, Find AD.
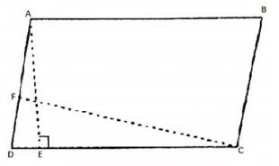
Solution:
Given that,
In parallelogram ABCD, CD = AB = 16 cm [∵ Opposite side of a parallelogramare equal]
We know that,
Area of parallelogram = Base × Corresponding altitude
Area of parallelogram ABCD = CD × AE = AD × CF
16 cm × cm = AD × 10 cm
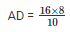 cm = 12.8 cm
cm = 12.8 cm
Thus, The length of AD is 12.8 cm.
Q 2. In Q 1, if AD = 6 cm, CF = 10 cm, and AE = 8 cm, Find AB.
Solution:
We know that,
Area of a parallelogram ABCD = AD × CF ⋅⋅⋅⋅⋅⋅⋅⋅⋅(1)
Again area of parallelogram ABCD = CD × AE⋅⋅⋅⋅⋅⋅⋅⋅⋅(2)
Compare equation(1) and equation(2)
AD × CF = CD × AE
⇒6×10 = D×8
⇒D = 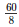 = 7.5 cm
= 7.5 cm
∴ AB = DC = 7.5cm [∵Opposite side of a parallelogramare equal]
Q 3. Let ABCD be a parallelogram of area 124 cm2 . If E and F are the mid-points of sides AB and CD respectively, then find the area of parallelogram AEFD.
Solution:
Given,
Area of a parallelogram ABCD = 124 cm2
Construction: Draw AP⊥DC
Proof:-
Area of a parallelogram AFED = DF × AP ⋅⋅⋅⋅⋅⋅⋅⋅⋅(1)
And area of parallelogram EBCF = FC × AP⋅⋅⋅⋅⋅⋅⋅⋅⋅(2)
And DF = FC ⋅⋅⋅⋅⋅⋅⋅⋅⋅(3) [FisthemidpointofDC]
Compare equation (1), (2) and (3)
Area of parallelogram AEFD = Area of parallelogram EBCF
∴ Area of parallelogram AEFD = 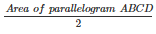
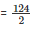 = 62cm2
= 62cm2
Q 4. If ABCD is a parallelogram, then prove that
Ar (ΔABD) = Ar (ΔBCD) = Ar (ΔABC) = Ar (ΔACD) = 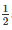 Ar(//gmABCD).
Ar(//gmABCD).
Solution:
Given:-
ABCD is a parallelogram,
To prove : – Ar (ΔABD) = Ar (ΔBCD) = Ar (ΔABC) = Ar (ΔACD) = 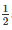 Ar(//gmABCD).
Ar(//gmABCD).
Proof:- We know that diagonal of a parallelogram divides it into two equilaterals .
Since, AC is the diagonal.
Then, Ar (ΔABC) = Ar (ΔACD) = 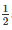 Ar(//gmABCD) ⋅⋅⋅⋅⋅⋅⋅⋅⋅(1)
Ar(//gmABCD) ⋅⋅⋅⋅⋅⋅⋅⋅⋅(1)
Since, BD is the diagonal.
Then , Ar (ΔABD) = Ar (ΔBCD) = 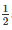 Ar(//gmABCD) ⋅⋅⋅⋅⋅⋅⋅⋅⋅(2)
Ar(//gmABCD) ⋅⋅⋅⋅⋅⋅⋅⋅⋅(2)
Compare equation (1) and (2)
∴ Ar (ΔABC) = Ar (ΔACD) = Ar (ΔABD) = Ar (ΔBCD) = 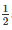 Ar(//gmABCD)..
Ar(//gmABCD)..
FAQs on Ex-15.2, Areas Of Parallelograms And Triangles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. How do you find the area of a parallelogram? |  |
| 2. How can we determine if two triangles are congruent? |  |
| 3. Can the area of a triangle be negative? |  |
| 4. How do you find the area of a triangle when only the side lengths are given? |  |
| 5. Is it possible for a parallelogram to have a right angle? |  |
















