Ex-16.4 (Part - 1), Circles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1) In figure 16.120, O is the centre of the circle. If ∠APB = 500,find ∠AOB and ∠OAB.
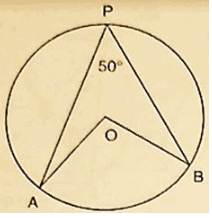
Solution:
∠APB = 500
by degree measure theorem
∠AOB = 2 ∠APB
⇒ ∠APB = 2×500 = 1000
since OA = OB [Radius of circle]
Then ∠OAB = ∠OBA [ Angles opposite to equalsides]
Let ∠OAB = x In ΔOAB, by Angles umproperty ∠OAB+ ∠OBA+ ∠AOB = 1800
= >x + x + 1000 = 1800
= >2x = 1800 – 1000
= >2x = 800
= >x = 400
∠OAB = ∠OBA = 400
Q2) In figure 16.121, it is given that O is the centre of the circle and ∠AOC = 1500.Find ∠ABC.
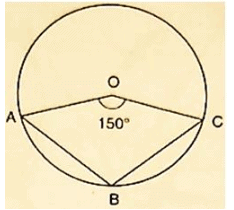
Solution:
∠AOC = 1500
∴ ∠AOC+reflex ∠AOC = 3600 [Complexangle]
⇒ 1500+reflex ∠AOC = 3600
⇒ reflex ∠AOC = 3600−1500
⇒ reflex ∠AOC = 2100
⇒ 2 ∠ABC = 2100 [ by degree measure theorem]
⇒ ∠ABC = 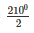 = 1050
= 1050
Q3) In figure 16.22, O is the centre of the circle. Find ∠BAC.
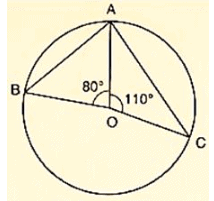
Solution:
We have ∠AOB = 800
and ∠AOC = 1100
Therefore, ∠AOB+ ∠AOC+ ∠BOC = 3600 [Completeangle]
⇒ 800+1000+ ∠BOC = 3600
⇒ ∠BOC = 3600−800−1100
⇒ ∠BOC = 1700
by degree measure theorem
∠BOC = 2 ∠BAC
⇒ 1700 = 2 ∠BAC
⇒ ∠BAC = 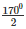 = 850
= 850
Q4) If O is the centre of the circle, find the value of x in each of the following figures.
(i)
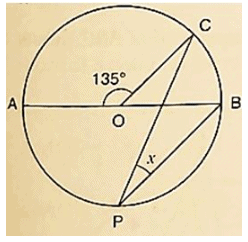
Solution:
∠AOC = 1350
∴ ∠AOC+ ∠BOC = 1800 [Linearpair of Angles ]
⇒ 1350 + ∠BOC = 1800
⇒ ∠BOC = 1800−1350
⇒ ∠BOC = 450
by degree measure theorem ∠BOC = 2 ∠CPB
⇒ 450 = 2x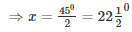
(ii)

Solution:
Wehave ∠ABC = 400 ∠ACB = 900 [Angle in semicircle]
In ΔABC, by Angles umproperty ∠CAB+ ∠ACB+ ∠ABC = 1800
⇒ ∠CAB+900+400 = 1800
⇒ ∠CAB = 1800−900−400
⇒ ∠CAB = 500
Now, ∠CDB = ∠CAB [Angleissameinsegment]
⇒ x = 500
(iii)

Solution:
Wehave ∠AOC = 1200 by degree measure theorem. ∠AOC = 2 ∠APC
⇒ 1200 = 2 ∠APC
⇒ ∠APC = 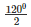 = 600
= 600
∠APC+ ∠ABC = 1800 [Opposite Angles of cyclicquadrilaterals]
⇒ 600+ ∠ABC = 1800
⇒ ∠ABC = 1800−600
⇒ ∠ABC = 1200
∴ ∠ABC+ ∠DBC = 1800 [Linearpair of Angles ]
⇒ 120+x = 1800
⇒ x = 1800−1200 = 600
(iv)
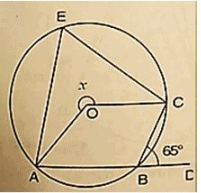
Solution:
Wehave ∠CBD = 650
∴ ∠ABC+ ∠CBD = 1800 [Linearpair of Angles ]
⇒ ∠ABC = 650 = 1800
⇒ ∠ABC = 1800−650 = 1150
∴reflex ∠AOC = 2 ∠ABC [ by degree measure theorem]
⇒ x = 2×1150
⇒ x = 2300
(v)
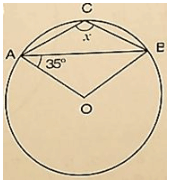
Solution:
Wehave ∠OAB = 350
Then, ∠OBA = ∠OAB = 350 [ Angles opposite to equalradii]
InΔAOB, by Angles umproperty
⇒ ∠AOB+ ∠OAB+ ∠OBA = 1800
⇒ ∠AOB+350+350 = 1800
⇒ ∠AOB = 1800−350−350 = 1100
∴ ∠AOB+reflex ∠AOB = 3600 [Complexangle]
⇒ 1100+reflex ∠AOB = 3600
⇒ reflex ∠AOB = 3600−1100 = 2500 by degree measure theoremreflex ∠AOB = 2 ∠ACB
⇒ 2500 = 2x
⇒ x = 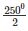 = 1250
= 1250
(vi)
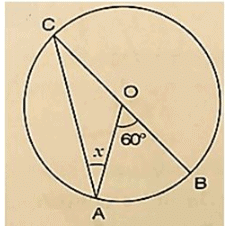
Solution:
Wehave ∠AOB = 600 by degree measure theoremreflex ∠AOB = 2 ∠ACB
⇒ 600 = 2 ∠ACB
⇒ ∠ACB = 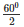 = 300 [ Angles opposite to equalradii]
= 300 [ Angles opposite to equalradii]
⇒ x = 300.
(vii)
Solution:
Wehave ∠BAC = 500 and ∠DBC = 700
∴ ∠BDC = ∠BAC = 500 [Angleinsamesegment]
InΔBDC, by Angles umproperty ∠BDC+ ∠BCD+ ∠DBC = 1800
⇒ 500+x+700 = 1800
⇒ x = 1800−500−700 = 600
(viii)

Solution:
Wehave, ∠DBO = 400 and ∠DBC = 900 [Angleinasemicircle]
⇒ ∠DBO+ ∠OBC = 900
⇒ 400+ ∠OBC = 900
⇒ ∠OBC = 900−400 = 500 by degree measure theorem
∠AOC = 2 ∠OBC
⇒ x = 2×500 = 1000
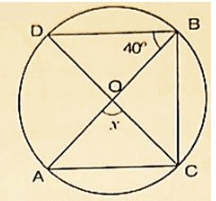
(ix)
Solution:
InΔDAB, by Angles umproperty ∠ADB+ ∠DAB+ ∠ABD = 1800
⇒ 320+ ∠DAB+500 = 1800
⇒ ∠DAB = 1800−320−500
⇒ ∠DAB = 980
Now, ∠OAB+ ∠DCB = 1800 [Opposite Angles of cyclicquadrilateral]
⇒ 980 + x = 1800
⇒ x = 1800−980 = 820
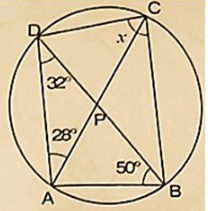
(x)
Solution:
Wehave, ∠BAC = 350
∠BDC = ∠BAC = 350 [Angleinsamesegment]
InΔBCD, by Angles umproperty ∠BDC+ ∠BCD+ ∠DBC = 1800
⇒ 350+x+650 = 1800
⇒ x = 1800−350−650 = 800
(xi)
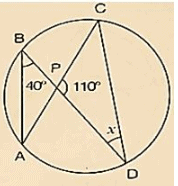
Solution:
Wehave, ∠ABD = 400
∠ACD = ∠ABD = 400 [Angleinsamesegment]
InΔPCD, by Angles umproperty
∠PCD+ ∠CPO+ ∠PDC = 1800
⇒ 400+1100+x = 1800
⇒ x = 1800−1500
⇒ x = 300
(xii)
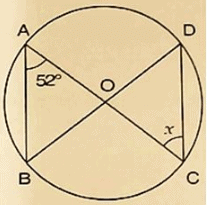
Solution:
Giventhat, ∠BAC = 520
Then ∠BDC = ∠BAC = 520 [Angleinsamesegment]
SinceOD = OC
Then ∠ODC = ∠OCD [Oppositeangle to equalradii]
⇒ x = 520
FAQs on Ex-16.4 (Part - 1), Circles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What are RD Sharma Solutions for Class 9 Maths? |  |
| 2. How can I access RD Sharma Solutions for Class 9 Maths? |  |
| 3. Are RD Sharma Solutions for Class 9 Maths useful for exam preparation? |  |
| 4. Can RD Sharma Solutions for Class 9 Maths be used for self-study? |  |
| 5. Are RD Sharma Solutions for Class 9 Maths available for free? |  |

|
Explore Courses for Class 9 exam
|

|

















