Ex-16.4 (Part - 2), Circles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q5) O is the circumference of the triangle ABC and Odis perpendicular on BC. Prove that ∠BOD = ∠A.
Solution:
Given O is the circum centre of triangle ABC and OD⊥BC
to prove ∠BOD = 2 ∠A
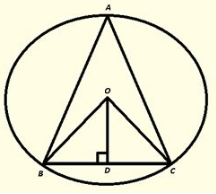
Pro of :
In ΔOBD and ΔOCD
∠ODB = ∠ODC [Each900]
OB = OC [Radius of circle]
OD = OD [Common]
ThenΔOBD≅ΔOCD [ by RHS Condition] .
∴ ∠BOD = ∠COD…..(i)
[PCT] . by degree measure theorem ∠BOC = 2 ∠BAC
⇒ 2 ∠BOD = 2 ∠BAC [ by using(i)]
⇒ ∠BOD = ∠BAC.
Q6) In figure 16.135, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = AC.
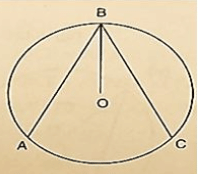
Solution:
Given, BO is the bisec to r of ∠ABC
to prove AB = BC
Pro of :
Since, BO is the bisec to r of ∠ABC.
Then, ∠ABO = ∠CBO…..(i)
Since, OB = OA [Radius of circle]
Then, ∠ABO = ∠DAB…..(ii) [opposite Angles to equal sides]
Since OB = OC [Radius of circle]
Then, ∠OAB = ∠OCB…..(iii) [opposite Angles to equal sides]
Compare equations (i), (ii) and (iii)
∠OAB = ∠OCB…..(iv)
InΔOAB andΔOCB
∠OAB = ∠OCB [From (iv)]
∠OBA = ∠OBC [Given]
OB = OB [Common]
Then, ΔOAB≅ΔOCB [ by AAScondition]
∴AB = BC [CPCT]
Q7) In figure 16.136, O is the centre of the circle, then prove that ∠x = ∠y+ ∠z.
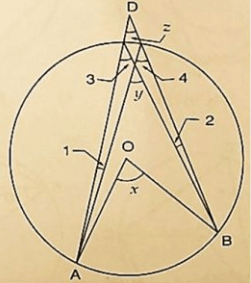
Solution:
We have,
∠3 = ∠4 [ Angles insamesegment]
∴ ∠x = 2 ∠3 [ by degree measure theorem]
⇒ ∠x = ∠3+ ∠3
⇒ ∠x = ∠3+ ∠4…..(i) [ ∠3 = angle4]
But ∠y = ∠3+ ∠1 [ by exteriorangleproperty]
⇒ ∠3 = ∠y− ∠1…..(ii)
from(i) and(ii)
∠x = ∠y− ∠1+ ∠4
⇒ ∠x = ∠y+ ∠4− ∠1
⇒ ∠x = ∠y+ ∠z+ ∠1− ∠1 [ by exteriorangleproperty]
⇒ ∠x = ∠y+ ∠z
Q8) In figure 16.137, O and O’ are centers of two circles intersecting at B and C. ACD is a straight line, find x.
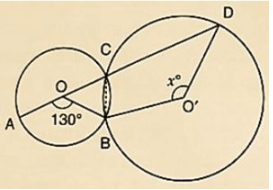
Solution:
by degree measure theorem ∠AOB = 2 ∠ACB
⇒ 1300 = 2 ∠ACB
⇒ ∠ACB = 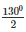 = 650
= 650
∴ ∠ACB+ ∠BCD = 1800 [Linerapair of Angles ]
⇒ 650+ ∠BCD = 1800
⇒ ∠BCD = 1800−650 = 1150 by degree measure theoremreflex ∠BOD = 2 ∠BCD
⇒ reflex ∠BOD = 2×1150 = 2300
Now,reflex ∠BOD+ ∠BO′D = 3600 [Complexangle]
⇒ 2300+x = 3600
⇒ x = 3600−2300
∴x = 1300
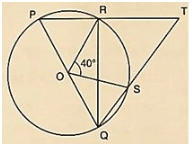
Q9) In figure 16.138, O is the centre of a circle and PQ is a diameter. If ∠ROS = 400,find ∠RTS..
Solution:
Since PQ is diameter
Then,
∠PRQ = 900 [Angleinsemicircle]
∴ ∠PRQ+ ∠TRQ = 1800 [Linearpair of angle]
900+ ∠TRQ = 1800
∠TRQ = 1800−900 = 900.
by degree measure theorem
∠ROS = 2 ∠RQS
⇒ 400 = 2 ∠RQS
⇒ ∠RQS = 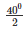 = 200
= 200
In ΔRQT, by Angle sum property
∠RQT+ ∠QRT+ ∠RTS = 1800
⇒ 200+900+ ∠RTS = 1800
⇒ ∠RTS = 1800−200−900 = 700
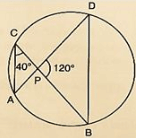
Q10) In figure 16.139, if ∠ACB = 400, ∠DPB = 1200,find ∠CBD.
Solution:
We have,
∠ACB = 400; ∠DPB = 1200
∴ ∠APB = ∠DCB = 400 [Angleinsamesegment]
InΔPOB, by Angles umproperty ∠PDB+ ∠PBD+ ∠BPD = 1800
⇒ 400+ ∠PBD+1200 = 1800
⇒ ∠PBD = 1800−400−1200
⇒ ∠PBD = 200
∴ ∠CBD = 200
Q11) A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
We have,
Radius OA = Chord AB
= >OA = OB = AB
Then triangle OAB is an equilateral triangle.
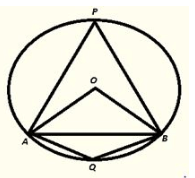
∴ ∠AOB = 600 [oneangle of equilateraltriangle]
by degree measure theorem
∠AOB = 2 ∠APB
⇒ 600 = 2 ∠APB
⇒ ∠APB = 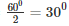
Now, ∠APB+ ∠AQB = 1800 [opposite Angles of cyclicquadrilateral]
⇒ 300+ ∠AQB = 1800
⇒ ∠AQB = 1800−300 = 1500.
Therefore, Angle by chord AB at minor arc = 1500
Angle by chord AB at major arc = 300
FAQs on Ex-16.4 (Part - 2), Circles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the concept of a circle in mathematics? |  |
| 2. How do we calculate the circumference of a circle? |  |
| 3. What is the relationship between the radius and diameter of a circle? |  |
| 4. How do we find the area of a circle? |  |
| 5. Can the circumference of a circle be greater than its area? |  |

|
Explore Courses for Class 9 exam
|

|

















