Ex-18.1, Basic Geometrical Tools, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
1.) Construct the following angles using set- squares:
Answer:
(i) 45o
Place 45o set- square.
Draw two rays AB and AC along the edges from the vertex from the vertex of 45o angle of the set- square.
The angle so formed is a 45o angle.
∠BAC=45o
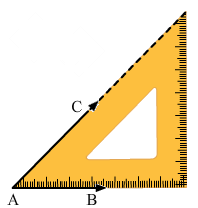
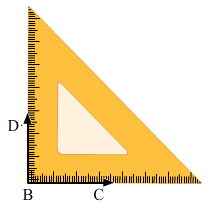
(ii) 90o
Place = 90o set –square as shown in the figure.
Draw two rays BC and BA along the edges from the vertex of 90o angle.
The angle so formed is 90o angle.
∠ABC=90o

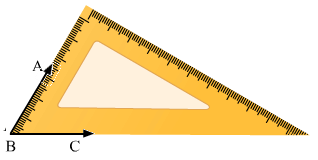
(iii) 60o
Place 30o set –square as shown in the figure.
Draw the rays BA and BC along the edges from the vertex of 60o
The angle so formed is 60o
∠ABC=60o
(iv) 105o
Place 30o set –square and make an angle 60o by drawing the rays BA and BC as shown in figure.
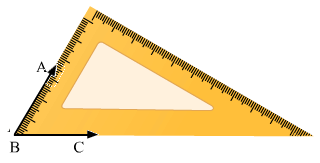
Now place the vertex of 45o of the set –square on the ray BA as shown in figure and draw the ray BD.
The angle so formed is 105o
Therefore, ∠DBC=105o

(v ) 75o
Place 45o set –square and make an angle of 45o by drawing the rays BD and BC as shown in the figure.
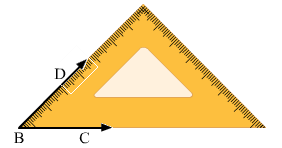
Now place the vertex of 30o of the set- square on the ray BD as shown in the figure and draw the ray BA.
The angle so formed is 75o.
Therefore, ∠ABC=75o
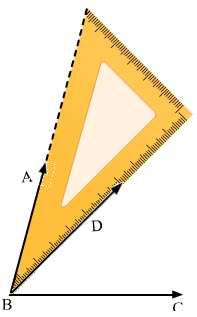
(Line BD is hidden)
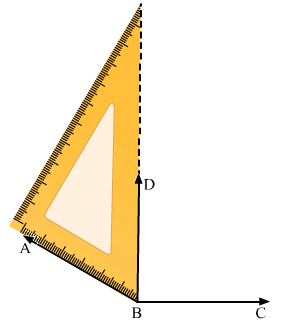
(vi) 150o
Place the vertex of 45o of the set – square and make angle of 90o by drawing the rays BD and BC as shown in the figure
Now, place the vertex of 30o of the set –square on the ray BS as shown in the figure and draw the ray BA
The angle so formed is 150o.
Therefore, ∠ABC=150o
2.) Given a line BC and a point A on it, construct a ray AD using set – squares so that ∠DAC is
(i) 30o
(ii) 150o
Answer:
(i) Draw a line BC and take a point A on it. Place 30o set –square on the line BC such that its vertex of 30o angle lies on point A and one edge coincides with the ray AB as shown in figure
Draw the ray AD.

Thus ∠DAC is the required angle of 30o
(ii) Draw a line BC and take a point A on it. Place 30o set –square on the line BC such that its vertex of 30o angle lies on point A and one edge coincides with the ray AB as shown in the figure.
Draw the ray AD.
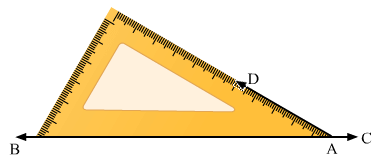
Therefore, ∠DAB=30o
We know that angle on one side of the straight line will always add to 180o
Therefore, ∠DAB+∠DAC=180o
Therefore, ∠DAC=150o
FAQs on Ex-18.1, Basic Geometrical Tools, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. What are the basic geometrical tools required for Class 6 Maths? |  |
| 2. How can I use a ruler to measure the length of a line segment? |  |
| 3. How can I use a compass to draw a circle? |  |
| 4. What is the purpose of a protractor in geometry? |  |
| 5. How can I use dividers to divide a line segment into equal parts? |  |

|
Explore Courses for Class 6 exam
|

|

















