Ex-19.2, (Part -1), Surface Area And Volume Of Right Circular Cylinder, Class 9 RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. A soft drink is available in two packs- (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm, Which container has greater capacity and by how much?
Solution:
Given,
The tin can will be cubical in shape.
Length (L) of tin can = 5 cm
Breadth (B) of tin can = 4 cm
Height (H) of tin can = 15 cm
Capacity of the tin can = l x b x h = (5 x 4 x 15) cm3
Radius (R) of the circular end of the plastic cylinder = 7/2 cm = 3.5 cm
Height (H) of plastic cylinder = 10 cm
Capacity of plastic cylinder 
Therefore, the plastic cylinder has greater capacity.
Difference in capacity = (385 – 300) cm3 = 85 cm3
Q2. The pillars of a temple are cylindrically shaped. If each pillar has a circular base of radius 20 cm and height 10 m, how much concrete mixture would be required to build 14 such pillars?
Solution:
Given,
The concrete mixture is used to build up the pillars is required for the entire space of the pillar i.e, we need to find the volume of the cylinders.
Radius of the base of a cylinder = 20 cm
Volume of the cylindrical pillar = πR2H

Therefore, volume of 14 pillars 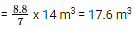
Q3. The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 gm.
Solution:
Given,
Inner radius (r1) of a cylindrical pipe = 24/2 = 12 cm
Outer radius (r2) of a cylindrical pipe = 24/2 = 14 cm
Height of pipe (h) = length of pipe = 35 cm
Mass of pipe = volume x density = 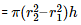
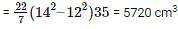
Mass of 1 cm3 wood = 0.6 gm
Therefore, mass of 5720 cm3 wood = 5720 x 0.6 = 3432 gm = 3.432 kg
Q4. If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, find:
(i) radius of its base
(ii) volume of the cylinder [Use pi = 3.141]
Solution:
(i) Given,
Height of the cylinder = 5 cm
Let radius of cylinder be ‘r’
Curved surface of the cylinder = 94.2 cm2
2 πrh = 94.2 cm2
r = 3 cm [π = 31.4, h = 5 cm]
(ii) Volume of the cylinder = πr2h = (3.14 x 32 x 5) cm3 = 141.3 cm3
Q5. The capacity of a closed cylindrical vessel of height 1 m is 15.4 liters. How many square meters of the metal sheet would be needed to make it?
Solution:
Given,
Height of the cylindrical vessel = 15.4 litres = 0.0154 m3 [1m3 = 1000 litres]
Let the radius of the circular ends of the cylinders be ‘r’
πr2h = 0.0154 m3
r = 0.07 m [π = 31.4, h =1m]
Total surface area of a vessel = 2πr(r+h)
= 2(3.14(0.07)(0.07+1)) m2 = 0.4703 m2
Q6. A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Solution:
Given,
Radius (R) of cylindrical bowl = 7/2 cm = 3.5 cm [Diameter = 7 cm]
Height up to which the bowl is filled with soup = 4 cm
Volume of soup in 1 bowl = πr2h

Volume of soup n 250 bowls = (250 x 154) cm3 = 38500 cm3 = 38.5 liters.
The hospital has to prepare 38.5 liters of soup daily in order to serve 250 patients.
Q7. A hollow garden roller, 63 cm wide with a girth of 440 cm, is made of 4 cm thick iron. Find the volume of the iron.
Solution:
Given, h = 63cm
The outer circumference of the roller = 440cm
Thickness of the roller = 4cm
Let, R be the external radius
We know that,
2πR = 440

R = 70
The thickness is given as 4cm, so the inner radius ‘r’ is given as
⇒ r = R – 4
⇒ = 70 – 4
⇒ = 66cm
Here, we know the inner and outer radii
So, the volume is given as
⇒ V = π(R2−r2)h

Q8. A solid cylinder has a total surface area of 231cm2. Its curved surface area is 3 of the total surface area. Find the volume of the cylinder.
Solution:
Given,
Total surface area = 231cm2
Curved surface area 

= 154
We know that,
2πrh + 2πr2 = 231 —– 1
Here 2πrh is the curved surface area, so substitute tha value of CSA in eq 1
⇒ 154 + 2πr2 = 231
⇒ 2πr2 = 231- 154
⇒ 2πr2 = 77

We need to find the value of h
CSA = 154cm2
⇒ 2πrh = 154
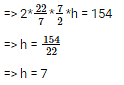
So the volume of the cylinder is,
Volume = πr2h
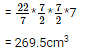
The volume of the cylinder is 269.5cm3
Q9. The cost of painting the total outside surface of a closed cylindrical oil tank at 50 paise per square decimetre is Rs 198. The height of the tank is 6 times the radius of the base of the tank. Find the volume corrected to 2 decimal places.
Solution:
Let the radius of the tank be r dm
Then, height = 6r dm
Cost of painting for 50 paisa per dm2 = Rs 198
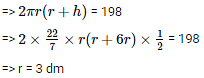
Therefore, h =(6 x 3) dm = 18 dm
Volume of the tank 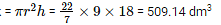
Q10. The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. Calculate the ratio of their volumes and the ratio of their curved surfaces.
Solution:
Let the radius of the cylinders be 2x and 3x and the height of the cylinders be 5y and 3y.

Q11.The ratio between the curved surface area and the total surface area of a right circular cylinder is 1:2. Find the volume of the cylinder, if its total surface area is 616cm2.
Solution:
Let, r be the radius of cylinder
h be the radius of cylinder
Total surface area (T.S.A) = 616cm2

Now,
TSA = 2πrh + 2πr2
⇒ 616 = CSA + 2πr2
⇒ 616 = 308 + 2πr2
⇒ 2πr2 = 616 – 308
⇒ 2πr2 = 308
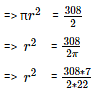
⇒ r = 7 cm
Since,CSA = 308cm2
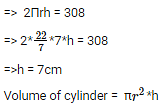
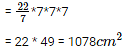
FAQs on Ex-19.2, (Part -1), Surface Area And Volume Of Right Circular Cylinder, Class 9 RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the formula for finding the surface area of a right circular cylinder? |  |
| 2. How do you calculate the volume of a right circular cylinder? |  |
| 3. Can you find the volume of a cylinder if only the height is given? |  |
| 4. How can the surface area of a cylinder be calculated if only the height is given? |  |
| 5. What is the relationship between the volume and surface area of a cylinder? |  |

|
Explore Courses for Class 9 exam
|

|

















