Ex-19.2, (Part -3), Surface Area And Volume Of Right Circular Cylinder, Class 9 RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q.23 A cylindrical container with diameter of base 56 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 32 cm x 22 cm x 14 cm . Find the rise in the level of the water when the solid is completely submerged.
Solution:
Given data is as follows :
Diameter of cylinder = 56 cm
Dimensions of rectangular block = 32 cm × 22 cm × 14 cm
We have to find the raise in the level of water in the cylinder .
First let us find the raise in the level of water in the cylinder . Diameter is given as 56 cm . Therefore ,
r = 28 cm
We know that the raise in the volume of water displaced in the cylinder will be equal to the volume of the rectangular block .
Let the raise in the level of water be h . Then we have ,
Volume of cylinder of height h and radius 28 cm = Volume of the rectangular block
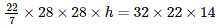
h = 4 cm
Therefore , the raise in the level of water when the rectangular block is immersed in the cylinder is 4 cm.
Q. 24. A cylindrical tube , open at both ends , is made of metal . The internal diameter of the tube is 10.4 cm and its length is 25 cm . The thickness of the metal is 8 mm everywhere . Calculate the volume of the metal .
Solution:
Given data is as follows :
Internal diameter = 10.4 cm
Thickness of the metal = 8 mm
Length of the pipe = 25 cm
We have to find the volume of the metal used in the pipe .
We know that ,
Volume of the hollow pipe = π(R2−r2)h
Given is the internal diameter which is equal to 10.4 cm .Therefore ,
r = 10.4/2
r = 5.2 cm
Also , thickness is given as 8 mm . Let us convert it to centimeters .
Thickness = 0.8 cm
Now that we know the internal radius and the thickness of the pipe , we can easily find external radius ‘R’ .
R = 5.2 + 0.8
R = 6 cm
Therefore , Volume of metal in the pipe 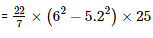
= 704 cm3
Therefore , the volume of metal present in the hollow pipe is 704 cm3 .
Q. 25 . From a tap of inner radius 0.75 cm , water flows at the rate of 7 m per second . Find the volume in litres of water delivered by the pipe in one hour .
Solution:
Given data is as follows :
r = 0.75 cm
Water flow rate = 7 m/sec
Time = 1 hour
We have to find the volume of water that flows through the pipe for 1 hour .
Let us first convert water flow from m/sec to cm/sec , since radius of the pipe is in centimeters
We have ,
Water flow rate = 7 m/sec
= 700 cm/sec
Volume of water delivered by the pipe is equal to the volume of a cylinder with h = 7 m and r = 0.75 cm . Therefore ,
Volume of water delivered in 1 second 
We have to find the volume of water delivered in 1hour which is nothing but 3600 seconds.
Therefore , we have
Volume of water delivered in 3600 seconds 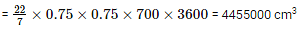
We know that 1000 cm3 = 1 litre
Therefore ,
Volume of water delivered in 1 hour = 4455 liters
Therefore , Volume of water delivered by the pipe in 1 hour is equal to 4455 liters.
Q. 26. A cylindrical water tank of diameter 1.4 m and height 2.1 m is being fed by a pipe of diameter 3.5 cm through which water flows at the rate of 2 metre per second . In how much time the tank will be filled ?
Solution:
Given data is as follows :
Diameter of the tank = 1.4 m
Height of the tank = 2.1 m
Diameter of the pipe = 3.5 cm
Water flow rate = 2 m/sec
We have to find the time required to fill the tank using the pipe .
The diameter of the tank is given which is 1.4 m . Let us find the radius .

Volume of the tank = πr2h
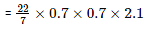
Given is the diameter of the pipe which is 3.5 cm . Therefore , radius is 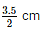 Let us convert it into metres . It then becomes
Let us convert it into metres . It then becomes 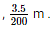
Volume of water that flows through the pipe in 1 second 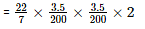
Let the time taken to fill the tank be x seconds . Then we have ,
Volume of water that flows through the pipe in x seconds 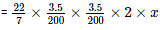
We know that volume of the water that flows through the pipe in x seconds will be equal to the volume of the tank . Therefore , we have
Volume of water that flows through the pipe in x seconds = Volume of the tank

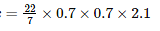
x = 1680 seconds
x = 1680/60 minutes
x = 28 minutes
Hence , it takes 28 minutes to fill the tank using the given pipe .
Q.27. A rectangular sheet of paper 30 cm x 18 cm can be transformed into the curved surface of a right circular cylinder in two ways i.e. , either by rolling the paper along its length or by rolling it along its breadth . Find the ratio of the volumes of the two cylinders thus formed .
Solution:
Given data is as follows :
Dimensions of the rectangular sheet of paper = 30 cm × 18 cm
We have to find the ratio of the volumes of the cylinders formed by rolling the sheet along its length and along its breadth .
Let V1 be the volume of the cylinder which is formed by rolling the sheet along its length .
When the sheet is rolled along its length , the length of the sheet forms the perimeter of the cylinder . Therefore , we have ,

The width of the sheet will be equal to the height of the cylinder . Therefore ,
h1 = 18 cm
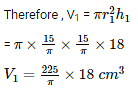
Let V2 be the volume of the cylinder formed by rolling the sheet along its width .
When the sheet is rolled along its width , the width of the sheet forms the perimeter of the base of the cylinder . Therefore , we have ,
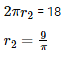
The length of the sheet will be equal to the height of the cylinder . Therefore ,
h2 = 30 cm
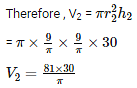
Now that we have the volumes of two cylinders , we have ,

Therefore , the ratio of the volumes of the two cylinders is 5 : 3 .
Q.28. How many litres of water flow out of a pipe having an area of cross-section of 5 cm2 in one minute , if the speed of water in the pipe is 30 cm/sec ?
Solution:
Given data is as follows :
Area of cross section of the pipe = 5 cm2
Speed of water = 30 cm/sec
We have to find the volume of water that flows through the pipe in 1 minute .
Volume of water that flows through the pipe in one second = πr2h
Here , πr2 is nothing but the cross section of the pipe and h is 30 cm .
Therefore , we have ,
Volume of water that flows through the pipe in one second = 5×30=150cm3
Volume of water that flows through the pipe in one minute = 150×60=9000cm3
We know that 1000 cm3 = 1 litre . Therefore ,
Volume of water that flows through the pipe in one minute = 9 litres
Hence , the volume of water that flows through the given pipe in 1 minute is 9 litres .
Q.29. The sum of the radius of the base and height of a solid cylinder is 37 m. If the total surface area of the solid cylinder is 1628 cm2 . Find the volume of the cylinder .
Solution:
Given data is as follows :
h + r = 37 cm
Total surface area of the cylinder = 1628 cm2
That is ,
2πrh+2πr2 = 1628
2πr(h+2r) = 1628
But it is already given in the problem that ,
h + r = 37 cm
Therefore , 2πr×37 = 1628
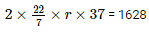
r = 7 cm
Since , h + r = 37 cm
We have , h + 7 = 37 cm
H = 30 cm
Now that we know both height and radius of the cylinder , we can easily find the volume .
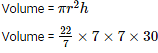
Volume = 4620 cm 3
Hence , the volume of the given cylinder is 4620 cm3 .
Q.30. Find the cost of sinking a tube well 280 m deep, having diameter 3 m at the rate of Rs 3.60 per cubic metre. Find also the cost of cementing its inner curved surface at Rs 2.50 per square metre .
Solution:
Given data is as follows :
Height of the tube well = 280 m
Diameter = 3 m
Rate of sinking of the tube well = Rs. 3.60/m3
Rate of cementing = Rs. 2.50/m2
Given is the diameter of the tub well which is 3 metres . Therefore
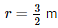
Volume of the tube well = πr2h
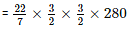
= 1980 m2
Cost of sinking the tube well = Volume of the tube well × Rate of sinking the tube well = 1980 × 3.60
= Rs . 7128
Curved surface area = 2πrh
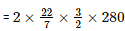
= 2640 m2
Cost of cementing = Curved Surface area × Rate of cementing
= 2640 × 2.50
= Rs . 6600
Therefore , the total cost of sinking the tube well is Rs . 7128 and the total cost of cementing its inner surface is Rs . 6600 .
Q.31. Find the length of 13.2 kg of copper wire of diameter 4 mm, when 1 cubic cm of copper weighs 8.4 gm .
Solution:
Given data is as follows :
Weight of copper wire = 13.2 kg
Diameter = 4 mm
Density = 8.4 gm /cm3
We have to find the length of the copper wire .
Given is the diameter of the wire which is 4 mm . Therefore ,
r = 2 mm
Let us convert r from millimeter to centimeter , since density is in terms of gm/cm3 . Therefore ,
r = 2/10 cm
Also , weight of the copper wire is given in kilograms . Let us convert into grams since density is in terms of gm/cm3 . Therefore , we have ,
Weight of copper wire = 13.2 × 1000 gm
= 13200 gm
We know that
Volume × Density = Weight
Therefore , πr2h×8.4 = 13.2
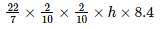
h = 12500 cm
h = 125 m
Hence , the length of the copper wire is 125 metres .
Q.32. A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
Solution:
Given data is as follows :
Inner diameter of the well = 10 m
Height = 8.4 m
Width of embankment = 7.5 m
We have to find the height of the embankment.
Given is the diameter of the well which is 10 m. Therefore ,
r = 5 m
The outer radius of the embankment,
R = Inner radius of the well + width of the embankment
= 5 + 7.5
= 12.5 m
Let H be the height of the embankment.
The volume of earth dug out is equal to the volume of the embankment . Therefore ,
Volume of embankment = Volume of earth dug out
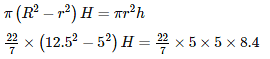
H = 1.6 m
Thus , height of the embankment is 1.6 m.
FAQs on Ex-19.2, (Part -3), Surface Area And Volume Of Right Circular Cylinder, Class 9 RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the formula for finding the surface area of a right circular cylinder? |  |
| 2. How do you find the volume of a right circular cylinder? |  |
| 3. Can you explain the concept of lateral surface area in a right circular cylinder? |  |
| 4. How can we calculate the total surface area of a right circular cylinder? |  |
| 5. Is there any relationship between the volume and surface area of a right circular cylinder? |  |

|
Explore Courses for Class 9 exam
|

|

















