Ex-2.4 Playing With Numbers, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
Q. 1.) In which of the following expressions, prime factorization has been done?
Answer: (i) 24 = 2 x 3 x 4 is not a prime factorization as 4 is not a prime number.
(ii) 56 = 1 x 7 x 2 x2 x 2 is not a prime factorization as 1 is not a prime number.
(iii) 70 = 2 x 5 x 7 is a prime factorization as 2, 5, and 7 are prime numbers.
(iv) 54 = 2 x 3 x 9 is not a prime factorization as 9 is not a prime number.
Q. 2.) Determine prime factorization of each of the following numbers:
Answer: (i) 216
We have:
| 2 | 216 |
| 2 | 108 |
| 2 | 54 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
Therefore, Prime factorization of 216 = 2 x 2 x 2 x3 x 3
(ii) 420
We have:
| 2 | 420 |
| 2 | 210 |
| 3 | 105 |
| 5 | 35 |
| 7 | 7 |
| 1 |
Therefore, Prime factorization of 420= 2 x 2 x 3 x 5 x 7
(iii) 468
We have:
| 2 | 468 |
| 2 | 234 |
| 3 | 117 |
| 3 | 39 |
| 13 | 13 |
| 1 |
Therefore, Prime factorization of 468 = 2 x 2 x 3 x 3 x 13
(iv) 945
We have:
| 3 | 945 |
| 3 | 315 |
| 3 | 105 |
| 5 | 35 |
| 7 | 7 |
| 1 |
Therefore, Prime factorization of 945 = 3 x 3 x 3 x 5 x 7
(v) 7325
We have:
| 5 | 7325 |
| 5 | 1465 |
| 293 | 293 |
| 1 |
Therefore, Prime factorization of 7325= 5 x 5 x 293
(vi) 13915
We have:
| 5 | 13915 |
| 11 | 2783 |
| 11 | 253 |
| 23 | 23 |
| 1 |
Therefore, Prime factorization of 13915 = 5 x 11 x 11 x 23
Q. 3.) Write the smallest 4-digit number and express it as a product of primes.
Answer: The smallest 4-digit number is 1000.
1000 = 2 x 500
=2 x2 x250
=2 x2 x2 x 125
=2 x2x2x5x 25
=2 x2x2x5x5x5
Therefore, 1000=2 x2 x2x5x5x5
Q. 4.) Write the largest 4-digit number and express it as product of primes.
Answer: The largest 4-digit number is 9999.
We have:
| 3 | 9999 |
| 3 | 3333 |
| 11 | 1111 |
| 101 | 101 |
| 1 |
Hence, the largest 4-digit number 9999 can be expressed in the form of its prime factors as 3 x 3 x 11 x 101.
Q. 5.) Find the prime factors of 1729. Arrange the factors in ascending order, and find the relation between two consecutive prime factors.
Answer: The given number is 1729.
We have:
| 7 | 1729 |
| 13 | 247 |
| 19 | 19 |
Thus, the number 1729 can be expressed in the form of its prime factors ass 7 x 13 x19.
Relation between its two consecutive prime factors:
The consecutive prime factors of the given number are 7, 13 and 19.
Clearly, 13 – 7 = 6 and 19 – 13 =6
Here, in two consecutive prime factors, the latter is 6 more than the previous one.
Q. 6.) Which factors are not included in the prime factorization of a composite number?
Answer: 1 and the number itself are not included in the prime factorization of a composite number.
Example: 4 is a composite number.
Prime factorization of 4 = 2 x 2.
Q. 7.) Here are two different factor trees for 60. Write the missing numbers:
Answer: (i) Since 6 = 2 x 3 and 10= 5 x 2. We have:
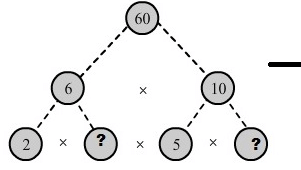
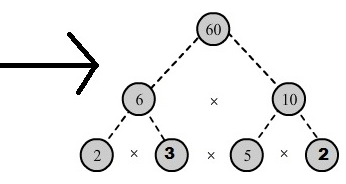
(ii) Since 60 = 30 x 2.
30= 10 x 3 and 10 = 5 x 2 we have:
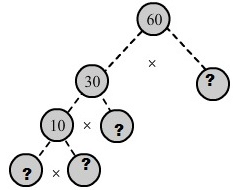
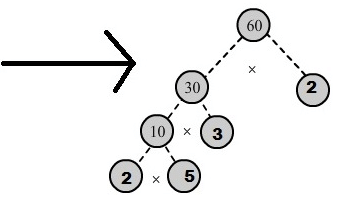
FAQs on Ex-2.4 Playing With Numbers, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. What is the importance of playing with numbers in Class 6 Maths? |  |
| 2. How can playing with numbers help improve problem-solving skills? |  |
| 3. What are the benefits of using RD Sharma Solutions for Class 6 Maths? |  |
| 4. How can playing with numbers make learning Maths more enjoyable? |  |
| 5. Are there any real-life applications of playing with numbers in Class 6 Maths? |  |

|
Explore Courses for Class 6 exam
|

|

















