Ex-20.1 (Part -2), Surface Area And Volume Of Right Circular Cone, Class 9, Mat RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 14: The diameters of two cones are equal. If their slant height are in the ratio 5:4,find the ratio of their curved surfaces.
Solution:
It is given that
Diameters of two cones are equal
Therefore their radius are also equal i.e
r1 = r2
Let the ratio of slant height be x
Therefore l1 = 5x
l2 = 4x
Therefore Ratio of curved surface area =
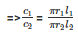
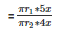
= 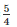
∴ Ratio of curved surface area is 5:4.
Q 15: Curved surface area of a cone is 308 cm2 and its slant height is 14cm. Find the radius of the base and total surface area of the cone.
Solution:
(1) It is given that
Slant height of cone = 14cm
Let radius of circular end of cone = r
Curved surface area of cone = πrl
⇒ 308 cm2 = 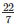 ∗r∗14
∗r∗14
⇒ r = 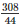 = 7cm
= 7cm
Thus radius of circular end of cone = 7 cm.
(ii) It is given that C.S.A = 308 cm2
We know that total surface area of a cone
= curved surface area of a cone + Area of base
= πrl + πr2
= [308 + (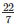 ∗72)]
∗72)]
= 308 + 154
= 462cm2
Thus total surface area of the cone is 462cm2
Q 16: The slant height and base diameter of a conical tomb are 25m and 14m respectively. Find the cost of white washing its curved surface area at the rate of Rs 210 per 100m2.
Solution:
It is given that
Slant height of conical tomb(l) = 25m
Base radius (r) of tomb = 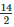 = 7m
= 7m
Curved surface area of conical length tomb = πrl
= 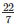 ∗7∗25
∗7∗25
= 550 m2
Cost of white washing 100 m2 area = Rs 210
Cost of white washing 550m2 area = 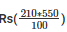 = Rs 1155
= Rs 1155
Therefore the cost of white washing the whole tomb is Rs 1155.
Q 17: A conical tent is 10 m high and the radius of it base is 24 m. Find the slant height of the tent. If the cost of 1m2 canvas is Rs 70, find the cost of canvas required for the tent.
Solution:
It is given that
Height of the conical tent(h) = 10m
Radius of conical tent(r) = 24m
Let slant height of conical tent be l
l2 = h2 + r2
= 102 + 242 = 100 + 576
= 676 m2
⇒ l = 26m
Thus,the slant height of the conical tent is 26m.
(ii) It is given that:
Radius(r) = 24 m
Slant height (l) = 26 m
C.S.A of tent = πrl
= 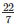 ∗24∗26
∗24∗26
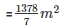
Cost of 1m2 canvas = Rs 70
Cost of 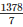 m2 canvas = Rs
m2 canvas = Rs 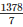 *70 = Rs 1,37,280
*70 = Rs 1,37,280
Thus the cost of canvas required to make the tent is Rs 1,37,280.
Q 18: A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11m while the vertex of the cone is 16 m above the ground. Find the area of the canvas required for the tent.
Solution:
It is given that
Diameter of cylinder = 24 m
therefore radius = 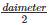
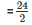 = 12 cm
= 12 cm
Also radius of cone = 12 m
Height of cylinder = 11 m
Height of cone = 16−11 = 5m
Slant height of cone
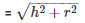
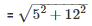
= 13m
Therefore area of canvas required for the tent = πrl + 2πrh
= 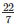 [(12∗13) + (2∗12∗11)] = 490.286 + 829.714
[(12∗13) + (2∗12∗11)] = 490.286 + 829.714
= 1320m2
Q19. A circus tent is cylindrical to a height of 3 m and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
Solution:
Given diameter = 105 m,
Radius = 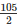 m = 52.5 m
m = 52.5 m
Therefore curved surface area of circus tent = πrl + 2πrh
= (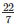 ∗52.5∗53) + (2∗
∗52.5∗53) + (2∗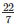 ∗52.5∗3)
∗52.5∗3)
= 8745 + 990 = 9735 m2
Therefore length of the canvas required for tent
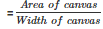
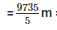 = 1947 m
= 1947 m
Q20 The circumference of the base of a 10m height conical tent is 44m, calculate the length of canvas used in making the tent if width of canvas is 2m.
Solution:
We know that
C.S.A of cone = πrl
Given circumference = 2πr
⇒ 2∗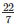 ∗r = 44
∗r = 44
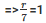
⇒ r = 7m
Therefore l = 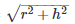
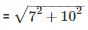
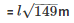
Therefore C.S.A of tent = πrl
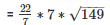
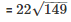
Therefore the length of canvas used in making the tent
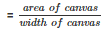
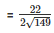

= 134.2 m
Q 21: What length of tarpaulin 4 m wide will be required to make a conical tent of height 8 m and base radius 6 m?Assume that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm.
Solution:
Given that,
Height of conical tent(h) = 8m
Radius of base of tent(r) = 6m
Slant height(l) = 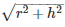
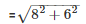
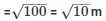
C.S.A of conical tent = πrl
= (3.14*6*10) m2 = 188.4 m2
Let the length of tarpaulin sheet required be l
As 20 cm will wasted ,so effective
Length will be (l – 0.2 m)
Breadth of tarpaulin = 3m
Area of sheet = C.S.A of sheet
[l*0.2*3]m = 188.4 m2 = l – 0.2 m = 62.8 m
Accounting extra for wastage:
⇒ l = 63 m
Thus the length of the tarpaulin sheet will be = 63 m
Q 22: A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled card board. Each cone has a base diameter of 40 cm and height 1m. If the outer side of each of the cones is to be painted and the cost of painting is Rs 12 per m2,what will be the cost of painting all these cones?
Solution:
The area to be painted is the curved surface area of each cone.
The formula of the curved surface area of a cone with base radius and slant height 7 is given as
Curved Surface Area = πrl
For each cone, we’re given that the base diameter is 0.40 m.
Hence the base radius r = 0.20 m.
The vertical height l 1 = 1 m.
To find the slant height ‘l’ to be used in the formula for Curved Surface Area we use the following relation
Slant height ,
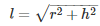
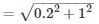
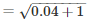
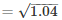
l = 1.02 m
Now substituting the values of r = 0.2 m and slant height 1 = 1.02 m and using pi = 3.14 in the formula of C.S.A.
We get Curved Surface Area = (3.14)(0.2)(1.02) = 0.64056 m2
This is the curved surface area of a single cone.
Since we need to paint 50 such cones the total area to be painted is,
Total area to be painted = (0.64056) (50) = 32.028 m2
The cost of painting is given as Rs. 12 per m2
Hence the total cost of painting = (12) (32.028) = 384.336
Hence, the total cost that would be incurred in the painting is Rs. 384.336
Q23. A cylinder and a cone have equal radii of their base and equal heights. If their curved surface area are in the ratio 8:5, show that the radius of each is to the height of each as 3:4.
Solution:
It is given that the base radius and the height of the cone and the cylinder are the same.
So let the base radius of each is ‘ r ‘ and the vertical height of each is ‘h’.
Let the slant height of the cone be ‘ l ’.
The curved surface area of the cone = πrl
The curved surface area of the cylinder = Extra close brace or missing open brace
It is said that the ratio of the curved surface areas of the cylinder to that of the cone is 8:5
So,
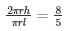
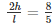

But we know that l =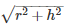
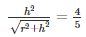
Squaring on both sides we get:


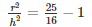
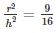
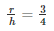
Hence it is shown that the ratio of the radius to the height of the cone as well as the cylinder is: 3 : 4
FAQs on Ex-20.1 (Part -2), Surface Area And Volume Of Right Circular Cone, Class 9, Mat RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the formula to find the surface area of a right circular cone? |  |
| 2. How do you calculate the volume of a right circular cone? |  |
| 3. Can you explain the concept of slant height in a right circular cone? |  |
| 4. How is a right circular cone different from a cylinder? |  |
| 5. How can the surface area and volume of a cone be useful in real-life applications? |  |

|
Explore Courses for Class 9 exam
|

|

















