Ex-20.1(Part - 1), Surface Area And Volume Of Right Circular Cone, Class 9, Mat RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1: Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
Solution:
It is given that :
Slant height of cone(l) = 60 cm
Radius of the base of the cone(r) = 21 cm
Curved surface area(C.S.A) = ?
C.S.A = πrl =  *21*60 = 3960cm2
*21*60 = 3960cm2
Therefore the curved surface area of the right circular cone is 3960cm2
Q 2 :The radius of a cone is 5cm and vertical height is 12cm. Find the area of the curved surface.
Solution:
It is given that:
Radius of cone (r) = 5 cm
Height of the tent (h) = 12 cm
Slant Height of tent (l) = ?
Curved surface area (C.S.A) = ?
Now we know we that,

l2 = r2 + h2
l2 = 52 + 122
l2 = = 25 + 144
⇒ l = 13 cm
Now,
C.S.A = πrl = 3.14*5*12 = 204.28cm2
Therefore the curved surface area of the cone is 204.28cm2
Q3 : The radius of a cone is 7 cm and area of curved surface is 176cm2 .Find the slant height.
Solution:
It is given that:
Radius of cone(r) = 7 cm
Curved surface area(C.S.A) = 176cm2
Slant Height of tent (l) = ?
Now we know,
C.S.A = πrl
⇒ πrl = 176
⇒  ∗7∗l = 176
∗7∗l = 176
 = 8 cm
= 8 cm
Therefore the slant height of the cone is 8 cm.
Q 4: The height of a cone 21 cm. Find the area of the base if the slant height is 28 cm.
Solution:
It is given that :
Height of the traffic cone(h) = 21 cm
Slant height of the traffic cone(l) = 28 cm
Now we know that,
l2 = r2 + h2
282 = r2 + 212
r2 = 282 − 212

Area of the circular base = πr2
 = 1078 cm2
= 1078 cm2
Therefore the area of the base is 1078cm2.
Q 5: Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
Solution:
It is given that :
Radius of the cone(r) = 6 cm
Height of the cone(h) = 8 cm
Total Surface area of the cone (T.S.A) = ?
l2 = r2 + h2
= 62 + 82
= 36 + 64 = 100
⇒ l = 10 cm
T.S.A = Curved surface area of cone + Area of circular base
= π∗r∗l + π∗r2
= (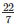 ∗6∗10) + (
∗6∗10) + (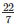 ∗6∗6)
∗6∗6)

= 301.171cm2.
Therefore the area of the base is 301.71cm2.
Q 6: Find the curved surface area of a cone with base radius 5.25 cm and slant height 10 cm.
Solution:
It is given that :
Base radius of the cone(r) = 5.25 cm
Slant height of the cone(l) = 10 cm
Curved surface area (C.S.A) = πrl
=  *5.25*10 = 165cm2.
*5.25*10 = 165cm2.
Therefore the curved surface area of the cone is 165cm2
Q 7: Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Solution:
It is given that :
Diameter of the cone(d) = 24 m
Radius of the cone(r) =  = 12m
= 12m
Slant height of the cone(l) = 21 m
T.S.A = Curved surface area of cone + Area of circular base
= π∗r∗l + π∗r2
= ( ∗12∗21) + (
∗12∗21) + ( ∗12∗12) =
∗12∗12) =  ∗12(12 + 21) = 1244.57m2.
∗12(12 + 21) = 1244.57m2.
Therefore the total surface area of the cone is 1244.57m2.
Q 8: The area of the curved surface of a cone is 60 π cm2 . If the slant height of the cone be 8 cm, find the radius of the base.
Solution:
It is given that :
Curved surface area(C.S.A) = 60 π cm2
Slant height of the cone(l) = 8 cm
Radius of the cone(r) = ?
Now we know,
Curved surface area(C.S.A ) = πrl
⇒ πrl = 60 π cm2
⇒ r*8 = 60
⇒ r = 7.5 cm
Therefore the radius of the base of the cone is 7.5 cm.
Q 9: The curved surface area of a cone is 4070 cm2 and diameter is 70 cm .What is its slant height?
Solution:
Diameter of the cone(d) = 70 cm
Radius of the cone(r) =  = 35cm
= 35cm
Slant height of the cone(l) = ?
Now,
Curved surface area = 4070cm2
⇒ πrl = 4070
Where, r = radius of the cone
l = slant height of the cone
Therefore πrl = 4070
⇒ 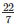 ∗35∗l = 4070
∗35∗l = 4070
 = 37 cm
= 37 cm
Therefore slant height of the cone is 37 cm.
Q 10: The radius and slant height of a cone are in the ratio 4:7.If its curved surface area is 792 cm2, find its radius.
Solution:
It is given that
Curved surface area = πrl = 792
Let the radius(r) = 4x
Height(h) = 7x
Now,
C.S.A = 792
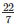 ∗4x∗7x = 792
∗4x∗7x = 792
⇒ 88x2 = 792
⇒ x2 =  = 9
= 9
⇒ x = 3
Therefore Radius = 4x = 4*3 = 12 cm
Q 11: A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Solution:
Given that,
Radius of conical cap(r) = 7 cm
Height of the conical cap(h) = 24 cm
Slant height(l) of conical cap =
 cm = 25 cm
cm = 25 cm
C.S.A of 1 conical cap = πrl
= 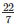 ∗7∗25
∗7∗25
= 550cm2
Curved surface area of 0 such conical caps = 5500 cm2
Thus, 5500 cm2 sheet will be required for making 10 caps.
Q 12: Find the ratio of the curved surface area of two cones if their diameter of the bases are equal and slant heights are in the ratio 4:3.
Solution:
Given that,
Diameter of two coins are equal.
Therefore their radius are equal.
Let r1 = r2 = r
Let ratio be x
Therefore slant height l1 of 1st cone = 4x
Similarly slant height l2 of 2nd cone = 3x
Therefore 


= 
Hence ratio is 4:3
Q 13: There are two cones .The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
Solution:
Let the curved surface area of 1st cone = 2x
C.S.A of 2nd cone = x
Slant height of 1st cone = h
Slant height of 2nd cone = 2h
Therefore 




Therefore ratio of r1 and r2 is 4:1.
FAQs on Ex-20.1(Part - 1), Surface Area And Volume Of Right Circular Cone, Class 9, Mat RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the formula for finding the surface area of a right circular cone? |  |
| 2. How is the volume of a right circular cone calculated? |  |
| 3. Can you explain the concept of slant height in a right circular cone? |  |
| 4. How do you find the height of a right circular cone if only the slant height and radius are known? |  |
| 5. Is the radius of the base the same as the slant height in a right circular cone? |  |

|
Explore Courses for Class 9 exam
|

|

















