Ex-21.2 (Part - 2), Surface Area And Volume Of Sphere, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q17. A cylindrical jar of radius 6 cm contains oil. Iron spheres each of radius 1.5 cm are immersed in the oil. How many spheres are necessary to raise the level of the oil by two centimeters?
Sol.
Given that,
Radius of the cylinder jar = 6cm = r1
Level to be rised = 2cm
Radius of each iron sphere = 1.5cm = r2
Numberofsphere = 



Numberofsphere = 16
Q18. A measuring jar of internal diameter 10 cm is partially filled with water. Four equal spherical balls of diameter 2 cm each are dropped in it and they sink down in water completely. What will be the change in the level of water in the jar?
Sol.
Given that,
Diameter of jar = 10cm
Radius of jar = 5cm
Let the level of water be raised by h
Diameter of the spherical bowl = 2cm
Radius of the ball = 1cm
Volume of jar = 4(Volume of spherical ball)


5×5×h = 4×
5×5×h = 4× ×1×1×1
×1×1×1


Heightofwaterinjar =  cm
cm
Q19. The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
Sol.
Given that
Diameter of sphere = 6cm
Radiusofsphere =  = 3cm = r1
= 3cm = r1
Diameterofthewire = 0.2cm
Radiusofthewire = 0.1cm = r2
Volume of sphere = Volume of wire

=  ×3×3×3 = 0.1×0.1×h
×3×3×3 = 0.1×0.1×h
h = 
h = 3600cmh = 36m
Therefore length of wire = 36m
Q20. The radius of the internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm respectively. If it is melted and recast into a solid cylinder of height 22/3cm. Find the diameter of the cylinder.
Sol.
Given that,
Internal radius of the sphere = 3cm = r1
External radius of the sphere = 5cm = r2
Height of the cylinder =  cm = h
cm = h
Volume of the spherical shell = Volume of cylinder



r3 = 
r3 = 7cm
Therefore diameter of the cylinder = 2(radius) = 14cm
Q21. A hemisphere of the lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
Sol. Given
Radius of the hemisphere = Volume of cone




r2 = 3.47cm
Therefore radius of the base = 3.74cm
Q22. A hollow sphere of internal and external radii 2cm and 4 cm respectively is melted into a cone of base radius 4cm. Find the height and slant height of the cone.
Sol.
Given that
Hollow sphere external radii = r2 = 4cm
Internal radii = r1 = 2cm
Cone base radius(R) = 4cm
Height = h
Volume of cone = Volume of sphere


h = 14cm
Slantheight(l) = 
Slantheight(l) = 
l =
l= 
l =
l = 14.56cm
Q23. A metallic sphere of radius 10.5 cm is melted and thus recast into small cones, each of radius 3.5 cm and height 3 cm. Find how many cones are obtained.
Sol.
Given that
Metallic sphere of radius = 10.5cm
Cone radius = 3.5cm
Height of radius = 3cm
Let the number of cones obtained be x
vs = x×vcone

x= 
x = 126
Therefore number of cones = 126
Q24. A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
Sol.
Given that
A cone and a hemisphere have equal bases and volumes
vcone = vhemisphere

r2h = 2r3
h = 2r

h : r = 2 : 1
Therefore the ratio is 2 : 1
Q25. A cone, a hemisphere, and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1 : 2 : 3.
Sol.
Given that
A cone, a hemisphere and a cylinder stand on one equal bases and have the same weight
We know that
vcone : vhemisphere : vcylinder

multiplying by 3
πr2h : 2πr3 : 3πr2hπr3 : 2πr3 : 3πr3 (∵ r = h and r2h = r3)
1 : 2 : 3
Thereforetheratiois1 : 2 : 3.
Q26. A cylindrical tub of radius 12 cm contains water to a depth of 20 cm. A spherical form ball is dropped into the tub and thus the level of water is raised by 6.75 cm. What is the radius of the ball?
Sol.
Radius of cylindrical tub = 12cm
Depth = 20cm
Let r be the radius of the ball
Then
Volume of the ball = Volume of water raised
 πr3 = πr2h
πr3 = πr2h
r3 =
r3 = 729
r= 
r = 9cm
Therefore radius of the ball = 9cm
Q27. The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Sol.
Side of cube = 10.5cm
Volume of sphere = v
Diameter of the largest sphere = 10.5cm
2r = 10.5
r = 5.25cm
Volumeofsphere = ×5.25×5.25×5.25
×5.25×5.25×5.25

v = 606.375cm3
Q28. A sphere, a cylinder, and a cone have the same diameter. The height of the cylinder and also the cone are equal to the diameter of the sphere. Find the ratio of their volumes.
Sol.
Let r be the common radius
Height of the cone = height of the cylinder = 2r
Let
v1 = Volume of sphere =  πr3
πr3
v1 = Volume of cylinder = πr2h = πr2×2r
v1 = Volume of cone = 
Now
v1 : v2 : v3 = 
= 4 : 6 : 2 = 2 : 3 : 1
Q29. A cube of side 4 cm contains a sphere touching its side. Find the volume of the gap in between.
Sol.
It is given that
Cube side = 4cm
Volume of cube = (4cm)3 = 64cm3
Diameter of the sphere = Length of the side of the cube = 4cm
Therefore radius of the sphere = 2cm
Volume of the sphere =  ×(2)3 = 33.52cm3
×(2)3 = 33.52cm3
Volume of gap = Volume of cube - Volume of sphere
= 64cm3 - 33.52cm3 = 30.48cm3
Q30. A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Sol.
Given that,
Inner radius of the hemispherical tank = 1m = r1
Thickness of the hemispherical tank = 1cm = 0.01m
Outer radius of hemispherical tank = (1+0.01) = 1.01m = = r2
Volume of iron used to make the tank = 


= 0.06348m3.
Q31. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (mm3) is needed to fill this capsule?
Sol.
Given that
Diameter of capsule = 3.5mm
Radius = = 1.75mm
= 1.75mm
Volume of spherical sphere =  πr3
πr3
 ×(1.75)3
×(1.75)3
= 22.458mm3
Therefore 22.46mm3 of medicine is required
Q32. The diameter of the moon is approximately one - fourth of the diameter of the earth. What is the earth the volume of the moon?
Sol.
Diameter of moon = 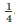 thdiameter of earth
thdiameter of earth
Let the diameter of earth be d, so radius = 
Then diameter of moon = 
Radius = 
Volume of moon =
Volume of earth = 

= 
Thus the volume of the moon is  of volume of earth
of volume of earth
FAQs on Ex-21.2 (Part - 2), Surface Area And Volume Of Sphere, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the formula for the surface area of a sphere? |  |
| 2. How do you find the volume of a sphere? |  |
| 3. Can you explain what surface area means in the context of a sphere? |  |
| 4. How is the surface area of a sphere related to its radius? |  |
| 5. How can the surface area and volume of a sphere be useful in real-life applications? |  |

|
Explore Courses for Class 9 exam
|

|

















