Ex-4.5, Operations On Whole Numbers, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
Q1. Without drawing a diagram, find:
Solution: (i) 10th square number:
A square number can easily be remembered by the following rule
Nth square number = n x n
10th square number = 10 x 10 = 100
(ii) 6th triangular number:
A triangular number can easily be remembered by the following rule
Nth triangular number = n x ( n + 1 )2
Therefore, 6th triangular number = 6 x ( 6 + 1 )2 = 21
Q2. (i) Can a rectangle number also be a square number ?
(ii) Can a triangular number also be a square number?
Solution: (i) Yes, a rectangular number can also be a square number; for example, 16 is a square number also a rectangular number.

(ii) Yes, there exists only one triangular number that is both a triangular number and a square number, and that number is 1.
Q3. Write the first four products of two numbers with difference 4 starting from in the following order:
1 , 2 , 3 , 4 , 5 , 6 , ………..
Identify the pattern in the products and write the next three products.
Solution: 1 x 5 = 5 (5 - 1 = 4)
2 x 6 = 12 (6 – 2 =4)
3 x 7 = 21 (7 – 3 = 4)
4 x 8 = 32 (8 – 4 = 4)
Q4. Observe the pattern in the following and fill in the blanks:
Solution: 9 x 9 + 7 =88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
Q5. Observe the following pattern and extend it to three more steps:
Solution: 6 x 2 – 5 = 7
7 x 3 – 12 = 9
8 x 4 – 21 = 11
9 x 5 – 32 = 13
10 x 6 – 45 = 15
11 x 7 – 60 = 17
12 x 8 – 77 = 19
Q6. Study the following pattern:
1 + 3 = 2 x 2
1 + 3 + 5 = 3 x 3
1 + 3 + 5 + 7 = 4 x 4
1 + 3 + 5 + 7 + 9 = 5 x 5
By observing the above pattern, find:
Solution: (i) 1 + 3 + 5 + 7 + 9 + 11
= 6 x 6
= 36
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15
= 8 x 8
= 64
(iii) 21 + 23 + 25 + ... + 51
= (21+23+25+...+51) can also be written as
(1+3+5+7+...+49+51) -(1+3+5+...+17+ 19)
(1+3 +5 +7+...+ 49 + 51)= 26 x 26 = 676
and, (1+3+5+...+17+ 19 ) = 10 x 10 = 100
Now,
( 21 + 23 +25 +...+ 51 )= 676 -100 = 576
Q7. Study the following pattern:
1x1 + 2x2 =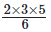
1x1 + 2x2 + 3x3 = 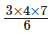
1x1 + 2 x 2 + 3 x 3 + 4 x 4 = 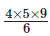
By observing the above pattern, write next two steps.
Solution: The next two steps are as follows:
1 x 1+2 x2+3 x 3+4 x4+5 x 5
=5x6x116
= 55
1 x 1+2 x2+3 x 3+4 x4+5 x 5+6 x6
=6x7x136
=91
Q8. Study the following pattern:
1 = 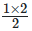
1 + 2 = 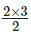
1 + 2 + 3 = 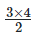
1 + 2 + 3 + 4 = 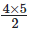 <
<
By observing the above pattern, find:
Solution: (i) 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
= 10 x 112
= 55
(ii) 50 + 51 + 52 + ...+ 100
This can also be written as
(1 + 2 + 3 + ...+ 99 + 100) - (1 + 2 + 3 + 4 + ...+ 47 + 49)
Now,
(1+ 2 + 3 + ...+ 99 + 100 ) = 100 x 1012
and, (1 + 2 + 3 + 4 +...+ 47 + 49 ) = 49 x 502
So, (50 + 51 + 52 + ...+ 100 ) = 100 x 1012 – 49 x 502
= 5050 - 1225
= 3825
(iii) 2 + 4 + 6 + 8 + 10 +...+ 100
This can also be written as 2 x (1 + 2 + 3 + 4 + ...+ 49 + 50)
Now,
(1 + 2 + 3 + 4 + ...+ 49 + 50 ) = 50 x 512
= 1275
Therefore, (2 + 4 + 6 + 8 + 10 + ...+ 100) = 2 x 1275 = 2550
FAQs on Ex-4.5, Operations On Whole Numbers, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. What are the different operations that can be performed on whole numbers? |  |
| 2. How can I add two whole numbers? |  |
| 3. How can I subtract one whole number from another? |  |
| 4. How can I multiply two whole numbers? |  |
| 5. How can I divide one whole number by another? |  |

|
Explore Courses for Class 6 exam
|

|

















