Ex-5.2, Factorization Of Algebraic Expressions, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1 . p3+27
SOLUTION :
= p3+33 ∵[a3+b3=(a+b)(a2−ab+b2)]
= (p + 3)(p² – 3p – 9)
∴ p3+27 =(p + 3)(p² – 3p – 9)
Q 2 . y3+125
SOLUTION :
= y3+53 ∵[a3+b3=(a+b)(a2−ab+b2)]
= (y+5)(y2−5y+52)
= (y+5)(y2−5y+25)
∴ y3+125 = (y+5)(y2−5y+25)
Q 3 . 1−27a3
SOLUTION :
= (1)3−(3a)3
= (1−3a)(12+1×3a+(3a)2) ∵[a3−b3=(a−b)(a2+ab+b2)]
= (1−3a)(12+3a+9a2)
∴ 1−27a3 = (1−3a)(12+3a+9a2)
Q 4 . 8x3y3+27a3
SOLUTION :
= (2xy)3+(3a)3
= (2xy+3a)((2xy)2−2xy×3a+(3a)2) ∵[a3+b3=(a+b)(a2−ab+b2)]
= (2xy+3a)(4x2y2−6xya+9a2)
∴ 8x3y3+27a3 = (2xy+3a)(4x2y2−6xya+9a2)
Q 5 . 64a3−b3
SOLUTION :
= (4a)3−b3
= (4a−b)((4a)2+4a×b+b2) ∵[a3−b3=(a−b)(a2+ab+b2)]
=(4a−b)(16a2+4ab+b2)
∴ 64a3−b3 =(4a−b)(16a2+4ab+b2)
Q 6 .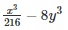 
SOLUTION :
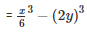
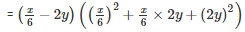∵ [x3−y3=(x−y)(x2+xy+y2)]
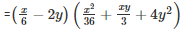
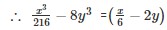
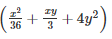
Q 7 . 10x4y−10xy4
SOLUTION :
= 10xy(x3−y3)
= 10xy(x−y)(x2+xy+y2) ∵[x3−y3=(x−y)(x2+xy+y2)]
∴ 10x4y−10xy4 = 10xy(x−y)(x2+xy+y2)
Q 8 . 54x6y+2x3y4
SOLUTION :
= 2x3y(27x3+y3)
= 2x3y((3x)3+y3)
= 2x3y(3x+y)((3x)2−3x×y+y2) ∵[a3+b3=(a+b)(a2−ab+b2)]
=2x3y(3x+y)(9x2−3xy+y2)
∴ 54x6y+2x3y4 =2x3y(3x+y)(9x2−3xy+y2)
Q 9 . 32a3+108b3
SOLUTION :
= 4(8a3+27b3)
= 4((2a)3+(3b)3)
= 4[(2a+3b)((2a)2−2a×3b+(3b)2)] ∵[a3+b3=(a+b)(a2−ab+b2)]
=4(2a+3b)(4a2−6ab+9b2)
∴ 32a3+108b3 =4(2a+3b)(4a2−6ab+9b2)
Q 10 . (a−2b)3−512b3
SOLUTION :
= (a−2b)3−(8b)3
= (a−2b−8b)((a−2b)2+(a−2b)8b+(8b)2) ∵[a3−b3=(a−b)(a2+ab+b2)]
=(a−10b)(a2+4b2−4ab+8ab−16b2+64b2)
=(a−10b)(a2+52b2+4ab)
∴ (a−2b)3−512b3 =(a−10b)(a2+52b2+4ab)
Q 11 . (a+b)3−8(a−b)3
SOLUTION :
= (a+b)3−[2(a−b)]3
= (a+b)3−[2a−2b]3
= (a+b−(2a−2b))((a+b)2+(a+b)(2a−2b)+(2a−2b)2) ∵[a3−b3=(a−b)(a2+ab+b2)]
=(a+b−2a+2b)(a2+b2+2ab+(a+b)(2a−2b)+(2a−2b)2)
=(a+b−2a+2b)(a2+b2+2ab+2a2−2ab+2ab−2b2+(2a−2b)2)
=(3b−a)(3a2+2ab−b2+(2a−2b)2)
=(3b−a)(3a2+2ab−b2+4a2+4b2−8ab)
=(3b−a)(3a2+4a2−b2+4b2−8ab+2ab)
=(3b−a)(7a2+3b2−6ab)
∴ (a+b)3−8(a−b)3 =(3b−a)(7a2+3b2−6ab)
Q 12 . (x+2)3+(x−2)3
SOLUTION :
= (x+2+x−2)((x+2)2−(x+2)(x−2)+(x−2)2) ∵[a3+b3=(a+b)(a2−ab+b2)]
=2x(x2+4x+4−(x+2)(x−2)+x2−4x+4)
=2x(2x2+8−(x2−22)) [∵(a+b)(a−b)=a2−b2]
=2x(2x2+8−x2+4)
=2x(x2+12)
∴ (x+2)3+(x−2)3 =2x(x2+12)
Q 13 . 8x2y3−x5
SOLUTION :
= x2((2y)3−x3)
= x2(2y−x)((2y)2+2y×x+x2) [∵x3−y3=(x−y)(x2+xy+y2)]
= x2(2y−x)(4y2+2xy+x2)
∴ 8x2y3−x5 = x2(2y−x)(4y2+2xy+x2)
Q 14 . 1029 – 3x3
SOLUTION :
= 3(343−x3)
= 3((7)3−x3)
= 3(7−x)(72+7x+x2) [∵a3−b3=(a−b)(a2+ab+b2)]
=3(7−x)(49+7x+x2)
∴ 1029 – 3x3 =3(7−x)(49+7x+x2)
Q 15 . x6+y6
SOLUTION :
= (x2)3+(y2)3
= (x2+y2)((x2)2−x2y2+(y2)2)
= (x2+y2)(x4−x2y2+y4) [∵a3+b3=(a+b)(a2−ab+b2)]
∴ x6+y6 = (x2+y2)(x4−x2y2+y4)
Q 16 . x3y3+1
SOLUTION :
= (xy)3+13
= (xy+1)((xy)2+xy+12) [∵x3+y3=(x+y)(x2−xy+y2)]
=(xy+1)(x2y2−xy+1)
∴ x3y3+1 = (xy+1)(x2y2−xy+1)
Q 17 . x4y4−xy
SOLUTION :
= xy(x3y3−1)
= xy((xy)3−13)
= xy(xy−1)((xy)2+xy×1+12) ∵[x3−y3=(x−y)(x2+xy+y2)]
=xy(xy−1)(x2y2+xy+1)
∴ x4y4−xy = xy(xy−1)(x2y2+xy+1)
Q 18 . a12+b12
SOLUTION :
= (a4)3+(b4)3
= (a4+b4)((a4)2−a4×b4+(b4)2) ∵[a3+b3=(a+b)(a2−ab+b2)]
=(a4+b4)(a8−a4b4+b8)
∴ a12+b12 = (a4+b4)(a8−a4b4+b8)
Q 19 . x3+6x2+12x+16
SOLUTION :
= x3+6x2+12x+8+8
= x3+3×x2×2+3×x×22+23+8
= (x+2)3+8 [∵a3+3a2b+3ab2+b3=(a+b)3]
= (x+2)3+23
= (x+2+2)((x+2)2−2(x+2)+22) ∵[a3+b3=(a+b)(a2−ab+b2)]
=(x+2+2)(x2+4+4x−2x−4+4) [∵(a+b)2=a2+b2+2ab]
=(x+4)(x2+4+2x)
∴ x3+6x2+12x+16 = (x+4)(x2+4+2x)
Q 20 . a3+b3+a+b
SOLUTION :
= (a3+b3)+1(a+b)
= (a+b)(a2−ab+b2)+1(a+b) [∵a3+b3=(a+b)(a2−ab+b2)]
=(a+b)(a2−ab+b2+1)
∴ a3+b3+a+b = (a+b)(a2−ab+b2+1)
Q 21 .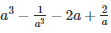 
SOLUTION :
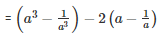
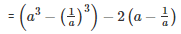
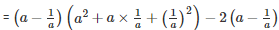
[∵a3−b3=(a−b)(a2+ab+b2)]
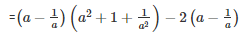
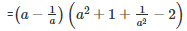
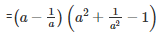
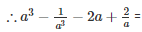
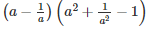
Q 22 . a3+3a2b+3ab2+b3−8
SOLUTION :
= (a+b)3−8 [∵a3+3a2b+3ab2+b3=(a+b)3]
=(a+b)3−23
=(a+b−2)((a+b)2+(a+b)×2+22)
= (a + b – 2)(a² + 2ab + b² + 2a + 2b + 4)
∴ a3+3a2b+3ab2+b3−8 = (a + b – 2)(a² + 2ab + b² + 2a + 2b + 4)
Q 23 . 8a3−b3−4ax+2bx
SOLUTION :
= (2a)3−b3−2x(2a−b)
= (2a−b)((2a)2+2a×b+b2)−2x(2a−b) [∵a3−b3=(a−b)(a2+ab+b2)]
=(2a−b)(4a2+2ab+b2−2x)
∴ 8a3−b3−4ax+2bx= (2a−b)(4a2+2ab+b2−2x)
Q 24 . i .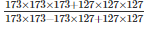
SOLUTION :
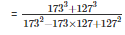
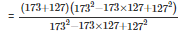∵[a3+b3=(a+b)(a2−ab+b2)]
=(173+127)
=300
Q 24 . ii .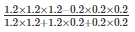
SOLUTION :
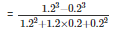
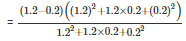[∵a3−b3=(a−b)(a2+ab+b2)]
=(1.2−0.2)
=1.0
Q 24 . iii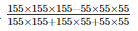 
SOLUTION :
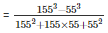
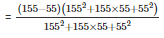[∵a3−b3=(a−b)(a2+ab+b2)]
= (155 – 55)
= 100
FAQs on Ex-5.2, Factorization Of Algebraic Expressions, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of factorization of algebraic expressions in class 9 mathematics? |  |
| 2. How can factorization of algebraic expressions be helpful in solving real-life problems? | |
| 3. Can you explain the process of factorization of algebraic expressions in class 9 mathematics? | |
| 4. What are some common factorization techniques used in class 9 mathematics? | |
| 5. Can you provide an example of factorization of an algebraic expression in class 9 mathematics? | |
|
4.69/5 Rating |
|
Dec 28, 2024 Last updated |
|
Explore Courses for Class 9 exam
|
|
Important questions
,past year papers
,video lectures
,Ex-5.2
,study material
,Ex-5.2
,Sample Paper
,Summary
,Free
,Viva Questions
,shortcuts and tricks
,Ex-5.2
,ppt
,Factorization Of Algebraic Expressions
,Factorization Of Algebraic Expressions
,Semester Notes
,Factorization Of Algebraic Expressions
,mock tests for examination
,MCQs
,practice quizzes
,Class 9
,Objective type Questions
,Previous Year Questions with Solutions
,Class 9
,Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics
,Extra Questions
,Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics
,Exam
,Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics
,Class 9
;
RD Sharma Solutions -Ex-5.2, Factorization Of Algebraic Expressions, Class 9, Maths Free PDF Download
Importance of RD Sharma Solutions -Ex-5.2, Factorization Of Algebraic Expressions, Class 9, Maths
RD Sharma Solutions -Ex-5.2, Factorization Of Algebraic Expressions, Class 9, Maths Notes
RD Sharma Solutions -Ex-5.2, Factorization Of Algebraic Expressions, Class 9, Maths Class 9 Questions
Study RD Sharma Solutions -Ex-5.2, Factorization Of Algebraic Expressions, Class 9, Maths on the App
|
© EduRev
|
Education Revolution
|
|
