Page No.9.14, Ratio Proportion And Unitary Method, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
PAGE NO 9.14:
Question 1: Which of the following statements are true?
(i) 16 : 24 = 20 : 30
(ii) 21 : 6 = 35 : 10
(iii) 12 : 18 = 28 : 12
(iv) 51 : 58 = 85 : 102
(v) 40 men : 200 men = Rs 5 : Rs 25
(vi) 99 kg : 45 kg = Rs 44 : Rs 20
ANSWER: (i) 16 : 24 = 20 : 30
16/24 = 2/3 (Dividing numerator and denominator by 8)
20/30 = 2/3 (Dividing numerator and denominator by 10)
∴ 16/24 = 20/30
Thus, the statement is true.
(ii) 21 : 6 = 35 : 10
21/6 = 7/2 (Dividing numerator and denominator by 3)
35/10 = 7/2 (Dividing numerator and denomenator by 5)
∴ 21/6 = 35/10
Thus, the statement is true.
(iii) 12 : 18 = 28 : 12
12/18 = 2/3 (Dividing numerator and denominator by 6)
28/12 = 7/3 (Dividing numerator and denominator by 4)
∴ 16/24 = 20/30 are not equal.
Thus, the statement is not true.
(iv) 51 : 58 = 85 : 102
51/58
And 85/102 = 5/6 (Dividing numerator and denominator by 17)
∴ 51/58 is not equal to 85/102.
Thus, the statement is not true.
(v) 40 men : 200 men = Rs 5 : Rs 25
40/200 = 1/5 (Dividing numerator and denominator by 40)
5/25 = 1/5 (Dividing numerator and denominator by 5)
∴ 40/200 = 5/25
Thus, the statement is true.
(vi) 99 kg : 45 kg = Rs 44 : Rs 20
99/45 = 11/5 (Dividing numerator and denominator by 9)
44/20 = 11/5 (Dividing numerator and denominator by 4)
∴ 99/45 = 11/5
Thus, the statement is true.
Question 2: Find which of the following are in proportion:
(i) 8, 16, 6, 12(ii) 6, 2, 4, 3
(iii) 150, 250, 200, 300
ANSWER: (i) Consider 8/16 = 1/2
And 6/12 = 1/2
∵ 8 : 16 = 6 : 12
∴ 8, 16, 6, 12 are in proportion.
(ii) Consider 6/2 = 3/1
And 4/3
∵ 6 : 2 ≠≠ 4 : 3
∴ 6, 2, 4, 3 are not in proportion.
(iii) Consider 150/250 = 3/5 (Dividing numerator and denominator by 50)
And 200/300 = 2/3 (Dividing numerator and denominator by 100)
∵ 150 : 250 ≠≠ 200 : 300
∴ 150, 250, 200, 300 are not in proportion.
Question 3: Find x in the following proportions:
(i) x : 6 = 55 : 11
(ii) 18 : x = 27 : 3
(iii) 7 : 14 = 15 : x
(iv) 16 : 18 = x : 96
ANSWER:
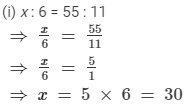
(ii) 18 : x = 27 : 3
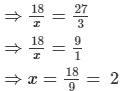
(iii) 7 : 14 = 15 : x1624=23 (Dividing numerator and denominator by 8)2030= 23 (Dividing numerator and denominator by 1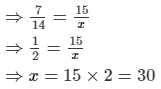
(iv) 16 : 18 = x : 96
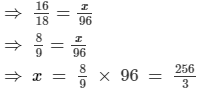
Question 4: Set up all proportions from the numbers 9, 150, 105, 1750.
ANSWER:
All proportions are:
9 : 150 = 3 : 50
9 : 105 = 3 : 35
9 : 1750
150 : 105 = 10 : 7
150 : 1750 = 3 : 35
105 : 1750 = 3 : 50
Thus, all proportions that can be formed are:
3 : 50, 3 : 35, 10 : 7, 9 : 1750, 1750 : 9, 7 : 10, 35 : 3 and 50 : 3
Question 5:
Find the other three proportions involving terms of each of the following:
(i) 45 : 30 = 24 : 16
(ii) 12 : 18 = 14 : 21
ANSWER: (i) 45 : 30 = 24 : 16 (3 : 2 is its simplest form)
Other three proportions are:
45 : 24 = 30 : 16 (15 : 8 is its simplest form)
30 : 45 = 16 : 24 (2 : 3 is its simplest form)
16 : 30 = 24 : 45 (8 : 15 is its simplest form)
(ii) 12 : 18 = 14 : 21 (2 : 3 is its simplest form)
Other three proportions are:
12 : 14 = 18 : 21 (6 : 7 is its simplest form)
21 : 18 = 14 : 12 (7 : 6 is its simplest form)
18 : 12 = 21 : 14 (3 : 2 is its simplest form)
Question 6: If 4, x, 9 are in continued proportion, find the value x.
ANSWER: It is given that 4, x, 9 are in continued proportion; therefore, we have:
4 : x : : x : 9
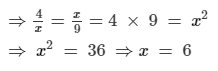
Question 7: If in a proportion, the first, second and fourth terms are 32, 112 and 217 respectively, find the third term.
ANSWER: In a proportion, the first, second and fourth terms are 32, 112 and 217, respectively.
Let the third term is be x.
Then, we have:
32 : 112 : : x : 217
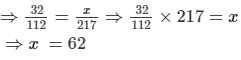
Question 8: Show that the following numbers are in continued proportion:
(i) 36, 90, 225
(ii) 48, 60, 75
(iii) 16, 84, 441
ANSWER: (i) 36, 90, 225
Consider 36/90 = 2/5 (Dividing numerator and denominator by 18)
90/225 = 2/5 (Dividing numerator and denominator by 45)
⇒ 36 : 90 : : 90 : 225
(ii) 48, 60, 75
Consider 48/60 = 4/5 (Dividing numerator and denominator by 12)
60/75 = 4/5 (Dividing numerator and denominator by 15)
⇒ 48 : 60 : : 60 : 75
(iii) 16, 84, 441
Consider 16/84 = 4/21 (Dividing numerator and denominator by 4)
84/441 = 4/21 (Dividing numerator and denominator by 4)
⇒ 16 : 84 : : 84 : 441
Question 9: The ratio of the length of a school ground to its width is 5 : 2. Find its length if the width is 40 metres.
ANSWER: Ratio of the length to the width of a school ground = 5 : 2
∵ Width = 40 m
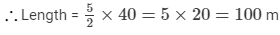
Question 10: The ratio of the sale of eggs on a Sunday to that of the whole week of a grocery shop was 2 : 9. If the total sale of eggs in the same week was Rs 360, find the sale of eggs on Sunday.
ANSWER: Ratio of the sale of eggs on Sunday to that of the whole week = 2 : 9
When total eggs of Rs. 9 is sold in a week, the sale of eggs on Sunday = Rs. 2
When total eggs of Rs. 1 sold in a week, th sale of eggs on Sunday = 2/9
When total eggs of Rs. 360 sold in a week, the sale of eggs on Sunday 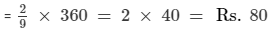
Question 11: The ratio of copper and zinc in an alloy is 9 : 7. If the weight of zinc in the alloy is 9.8 kg, find the weight of copper in the alloy.
ANSWER: The ratio of copper and zinc in an alloy is 9 : 7.
When the weight of zinc is 7 kg, the weight of copper = 9 kg
When the weight of zinc is 1 kg, the weight of copper = 9/7 kg
When the weight of zinc is 9.8 kg, the weight of copper =
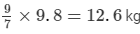
Question 12: The ratio of the income to the expenditure of a family is 7 : 6. Find the saving if the income is Rs 1400.
ANSWER: The ratio of the income to the expenditure of a family is 7 : 6.
∴ Ratio of saving to the income = (7 − 6) : 7 = 1 : 7 (Saving = Total income −- Expenditure)
∵ Income of the family = Rs. 1400
∴ Saving = 1400 × 17 = Rs. 200
Question 13: The ratio of story books in a library to other books is 1 : 7. The total number of story books is 800. Find the total number of books in the library.
ANSWER:
The ratio of story books in a library to other books is 1 : 7.
Out of (1 + 7) = 8 books, 1 book is a story book
Therefore,
When number of story books is 1, the total number of books = 8
When number of story books is 800, the total number of books = 8 × 800
= 6400
FAQs on Page No.9.14, Ratio Proportion And Unitary Method, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. What is the importance of understanding ratio and proportion in mathematics? |  |
| 2. How can I solve problems using the unitary method? |  |
| 3. Can you give an example of a real-life situation where ratio and proportion are used? |  |
| 4. How do I simplify ratios? |  |
| 5. Is it possible for two ratios to be equal even if the individual numbers are different? |  |






















