RD Sharma Solutions (Ex.1.1): Rational Numbers | RD Sharma Solutions for Class 8 Mathematics PDF Download
Q1. Add the following rational numbers:
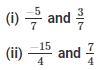
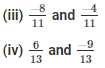
Solution:
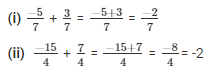
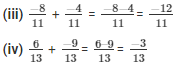
Q2: Add the following rational numbers:
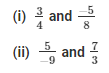
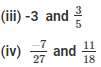
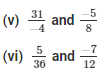
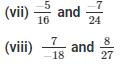
Solution:
(i) Clearly, denominators of the given numbers are positive.
The LCM of the denominators 4 and 8 is 8.
Now, we will express 3/4 in the form in which it takes the denominator as 8.
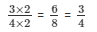
Now,
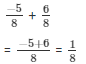
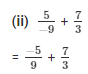
The LCM of the denominators 9 and 3 is 9.
Now,
We will express 7/3 in the form in which it takes denominator as 9.
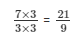
So,
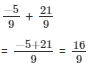
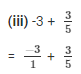
The LCM of the denominators 1 and 5 is 5.
Now,
We will express -3/1 in the form in which it takes denominator as 5.
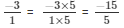
So,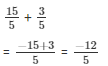
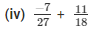
The LCM of the denominators 27 and 18 is 54.
Now,
We will express 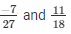 in the form in which it takes denominator as 54.
in the form in which it takes denominator as 54.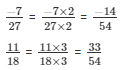
So,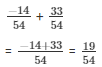
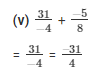
The LCM of the denominators 4 and 8 is 8.
Now,
We will express -31/4 in the form in which it takes denominator as 8.

So,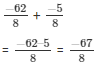
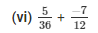
The LCM of the denominator 12 and 36 is 36.
Now,
We will express -7/12 in the form in which it takes denominator as 36.
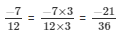
So,
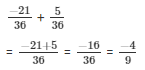
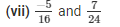
The LCM of the denominators 16 and 26 is 48.
Now,
We will express 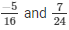 in the form in which it takes denominator as 48.
in the form in which it takes denominator as 48.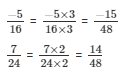
So,
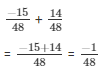
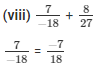
The LCM of the denominator 18 and 27 is 54.
Now,
We will express  in the form in which it takes denominator as 54.
in the form in which it takes denominator as 54.
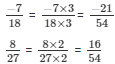
So,
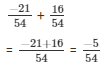
Q-3. Simplify:
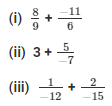
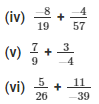
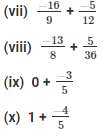
Solution:
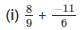
The LCM of the denominator 9 and 6 is 18.
Now,
We will express 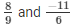 in the form in which it takes denominator as 18.
in the form in which it takes denominator as 18.
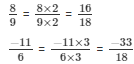
So,
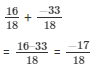
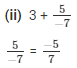
The LCM of the denominator 1 and 7 is 7.
Now,
We will express 3/1 in the form in which it takes denominator as 7.
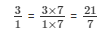
So,
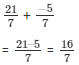
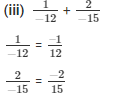
The LCM of the denominators 12 and 15 is 60.
Now,
We will express 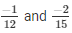 in the form in which it takes denominator as 60.
in the form in which it takes denominator as 60.
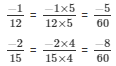
So,
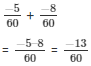
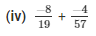
The LCM of the denominator of 19 and 57 is 57.
Now,
We will express -8/19 in the form in which it takes denominator as 57.
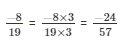
So,
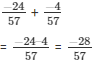
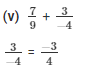
The LCM of the denominator 9 and 4 is 36.
Now,
We will express 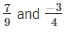 in the form in which it takes denominator as 36.
in the form in which it takes denominator as 36.
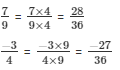
So,
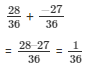
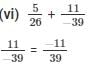
The LCM of the denominator 26 and 39 is 78.
Now,
We will express 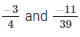 in the form in which it takes denominator as 78.
in the form in which it takes denominator as 78.
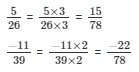
So,
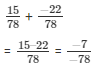
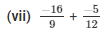
The LCM of the denominator 9 and 12 is 36.
Now,
We will express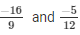 in the form in which it takes denominator as 36.
in the form in which it takes denominator as 36.
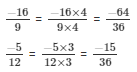
So,
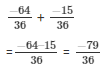
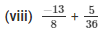
The LCM of the denominator 8 and 36 is 72.
Now,
We will express 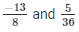 in the form in which it takes denominator as 72.
in the form in which it takes denominator as 72.
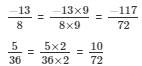
So,
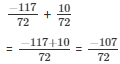
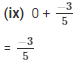
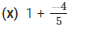
The LCM of the denominator 1 and 5 is 5.
Now,
We need to express 1/1 in the form in which it takes denominator as 5.
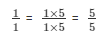
So,
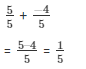
Q-4. Add and express the sum as a mixed fraction:
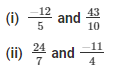
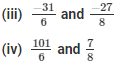
Solution:
(i) We have:
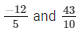
The LCM of the denominator 5 and 10 is 10.
Now,
We will express -12/5 in the form in which it takes denominator as 10.
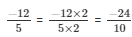
So,
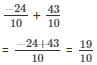
(ii) We have:
24/7 and -11/7
The LCM of the denominator 7 and 4 is 28.
Now,
We will express 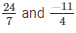 in the form in which it takes denominator as 10.
in the form in which it takes denominator as 10.
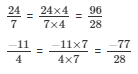
So,
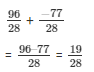
(iii) We have:
-31/6 and -27/8
The LCM of the denominator 6 and 8 is 24.
Now,
We will express -31/6 and -27/8 in the form in which it takes denominator as 24.
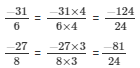
So,
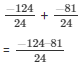
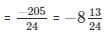
(iv) We have:
101/6 and 7/8
The LCM of the denominator 6 and 8 is 24.
Now,
We will express 101/6 and 7/8 in the form in which it takes denominator as 24.
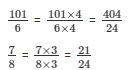
So,
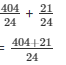
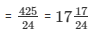
FAQs on RD Sharma Solutions (Ex.1.1): Rational Numbers - RD Sharma Solutions for Class 8 Mathematics
| 1. What are rational numbers? |  |
| 2. How do you determine if a number is rational? |  |
| 3. How can rational numbers be represented on a number line? |  |
| 4. What is the difference between rational and irrational numbers? |  |
| 5. How can rational numbers be operated upon? |  |

|
Explore Courses for Class 8 exam
|

|


















