Chapter 14 - Compound Interest (Part - 3), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 14.20:
Question 1:
On what sum will the compound interest at 5% per annum for 2 years compounded annually be Rs 164?
ANSWER:
Let the sum be Rs x.
We know that:CI = A − P
= P(1 + R/100)n − P
= P[(1 + R/100)n − 1]
164 = x[(1 + 5/100)² − 1]
164 = x[(1.05)² − 1]
x = 164/0.1025
= 1,600
Thus, the required sum is Rs 1,600.
PAGE NO 14.20:
Question 2:
Find the principal if the interest compounded annually at the rate of 10% for two years is Rs 210.
ANSWER:
Let the sum be Rs x.
We know that:CI = A − P
= P(1 + R/100)n − P
= P[(1 + R/100)n − 1]
210 = x[(1 + 10/100)² − 1]
210 = x[(1.10)² − 1]
x = 210/0.21
= 1,000
Thus, the required sum is Rs 1,000.
PAGE NO 14.20:
Question 3:
A sum amounts to Rs 756.25 at 10% per annum in 2 years, compounded annually. Find the sum.
ANSWER:
Let the sum be Rs x.
Then,A = P(1 + R/100)n
= P[(1 + R/100)n]
756.25 = x[(1 + 10/100)²]
756.25 = x[(1.10)²]
x = 756.25/1.21 = 625
Thus, the required sum is Rs 625.
PAGE NO 14.20:
Question 4:
What sum will amount to Rs 4913 in 18 months, if the rate of interest is 12(1/2)% per annum, compounded half-yearly?
ANSWER:
Let the sum be Rs x.
Given: A = Rs 4913
R = 12.5%
n = 18 months = 1.5 years
We know that:A = P(1 + R/200)²n
4,913 = P(1 + R/200)²n
4,913 = x(1 + 12.5/200)³
4,913 = x[(1.0625)³]
x = 4,913/1.1995 = 4,096
Thus, the required sum is Rs 4,096.
PAGE NO 14.20:
Question 5:
The difference between the compound interest and simple interest on a certain sum at 15% per annum for 3 years is Rs 283.50. Find the sum.
ANSWER:
Given:CI − SI = Rs 283.50
R = 15%
n = 3 years
Let the sum be Rs x.
We know that:A = P(1 + R/100)n
= P(1 + R/100)n
= x(1 + 15/100)³
= x(1.15)³ ...(1)
Also,
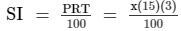= 0.45 x
A = SI + P = 1.45x ...(2)
Thus, we have:x(1.15)³ − 1.45x = 283.50 [From (1) and (2)]
1.523x − 1.45x = 283.50
0.070875x = 283.50
x = 283.50/0.070875 = 4,000
Thus, the sum is Rs 4,000.
PAGE NO 14.20:
Question 6:
Rachana borrowed a certain sum at the rate of 15% per annum. If she paid at the end of two years Rs 1290 as interest compounded annually, find the sum she borrowed.
ANSWER:
Let the money borrowed by Rachana be Rs x.
Then, we have:CI = P(1 + R/100)n − P
1,290 = x[(1 + 15/100)² − 1]
1,290 = x[0.3225]
x = 1,290/0.3225
= 4,000
Thus, Rachana borrowed Rs 4,000.
PAGE NO 14.20:
Question 7:
The interest on a sum of Rs 2000 is being compounded annually at the rate of 4% per annum. Find the period for which the compound interest is Rs 163.20.
ANSWER:
Let the time period be n years.
Then, we have:CI = P(1 + R/100)n − P
163.20 = 2,000(1 + 4/100)n − 2,000
2,163.20 = 2,000(1.04)n
(1.04)n = 2,163.20/2,000
(1.04)n = 1.0816
(1.04)n = (1.04)²
On comparing both the sides, we get:n = 2
Thus, the required time is two years.
PAGE NO 14.20:
Question 8:
In how much time would Rs 5000 amount to Rs 6655 at 10% per annum compound interest?
ANSWER:
Let the time period be n years.
Thus, we have:CI = P(1 + R/100)n − P
6,655 = 5,000(1 + 10/100)n − 5,000
11,655 = 5,000(1.10)n
(1.1)n = 11,655/5,000
(1.1)n = 2.331(1.1)n = (1.1)³
On comparing both the sides, we get:n = 3
Thus, the required time is three years.
PAGE NO 14.20:
Question 9:
In what time will Rs 4400 become Rs 4576 at 8% per annum interest compounded half-yearly?
ANSWER:
Let the time period be n years.
R = 8% = 4% (Half − yearly)
Thus, we have:A = P(1 + R/100)n
4,576 = 4,400(1 + 4/100)n
4,576 = 4,400(1.04)n
(1.04)n = 4,576/4,000
(1.04)n = 1.04
(1.04)n = 1.041
On comparing both the sides, we get: n = 1
Thus, the required time is half a year.
PAGE NO 14.20:
Question 10:
The difference between the S.I. and C.I. on a certain sum of money for 2 years at 4% per annum is Rs 20. Find the sum.
ANSWER:
Given:CI − SI = Rs 20
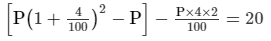
P[(1.042 − 1)] − 0.08P = 20
0.0816 P − 0.08 P = 20
0.0016 P = 20
P = 20/0.0016
= 12,500
Thus, the required sum is Rs 12,500.
PAGE NO 14.20:
Question 11:
In what time will Rs 1000 amount to Rs 1331 at 10% per annum, compound interest?
ANSWER:
Let the time be n years.Then,A = P(1 + 10/100)n
1,331 = 1,000(1 + 10/100)n
(1.1)n = 1,331/1,000
(1.1)n = 1.331
(1.1)n = (1.1)³
On comparing both the sides, we get:n = 3
Thus, the required time is three years.
NO 14.20:
Question 12:
At what rate percent compound interest per annum will Rs 640 amount to Rs 774.40 in 2 years?
ANSWER:
Let the rate of interest be R%.
Then,A = P(1 + R/100)n
774.40 = 640(1 + R/100)²
(1 + R/100)² = 774.40/640
(1 + R/100)² = 1.21
(1 + R/100)² = (1.1)²
(1 + R/100) = 1.1
R/100 = 0.1
R = 10
Thus, the required rate of interest is 10% per annum.
PAGE NO 14.20:
Question 13:
Find the rate percent per annum if Rs 2000 amount to Rs 2662 in 1.5 years, interest being compounded half-yearly?
ANSWER:
Let the rate of interest be R%.
Then,A = P(1 + R/100)n
2,662 = 2,000(1 + R/100)³
(1 + R/100)³ = 2,662/2,000
(1 + R/100)³ = 1.331
(1 + R/100)³ = (1.1)³
(1 + R/100) = 1.1
R/100 = 0.1
R = 10
Because the interest rate is being compounded half − yearly, it is 20% per annum.
PAGE NO 14.20:
Question 14:
Kamala borrowed from Ratan a certain sum at a certain rate for two years simple interest. She lent this sum at the same rate to Hari for two years compound interest. At the end of two years she received Rs 210 as compound interest, but paid Rs 200 only as simple interest. Find the sum and the rate of interest.
ANSWER:
Let the sum be Rs P and the rate of interest be R%.
We know that Kamla paid Rs 200 as simple interest.
∴ 200 = PR(2)/100
PR = 10,000 ...(1)
Also, Kamla received Rs 210 as compound interest.
∴ 210 = P(1 + R/100)² − 1
210(10,000) = P(R2 + 200R)
210R = R2 + 200R [from (1)]
R = 10% p.a.
Putting the equation in (1),
we get:P = 1,000
Thus, the required sum is Rs 1,000 and the rate of interest is 10%
PAGE NO 14.20:
Question 15:
Find the rate percent per annum, if Rs 2000 amount to Rs 2315.25 in an year and a half, interest being compounded six monthly.
ANSWER:
Let the rate percent per annum be R.
Because interest is compounded every six months, n will be 3 for 1.5 years.
Now,A = P(1 + R200)n
2,315.25 = 2,000(1 + R/200)³
(1 + R/200)³ = 2,315.25/2,000
(1 + R/200)³ = 1.157625
(1 + R/200)³ = (1.05)³
1 + R/200 = 1.05
R/200 = 0.05
= 10
Thus, the required rate is 10% per annum.
PAGE NO 14.20:
Question 16:
Find the rate at which a sum of money will double itself in 3 years, if the interest is compounded annually.
ANSWER:
Let the rate percent per annum be R.
Then,A = P(1 + R/100)n2
P = P(1 + R/100)³
(1 + R/100)³ = 2
(1 + R/100) = 1.2599
R/100 = 0.2599
R = 25.99
Thus, the required rate is 25.99% per annum.
PAGE NO 14.21:
Question 17:
Find the rate at which a sum of money will become four times the original amount in 2 years, if the interest is compounded half-yearly.
ANSWER:
Let the rate percent per annum be R.
Then,A = P(1 + R)²n
4P = P(1 + R/200)4
(1 + R/200)4 = 4
(1 + R/200) = 1.4142
R/200 = 0.4142
R = 82.84
Thus, the required rate is 82.84%.
PAGE NO 14.21:
Question 18:
A certain sum amounts to Rs 5832 in 2 years at 8% compounded interest. Find the sum.
ANSWER:
Let the sum be P.
Thus, we have:A = P(1 + R/100)n
5,832 = P(1 + 8/100)²
5,832 = 1.1664P
P = 5,832/1.1664
= 5,000
Thus, the required sum is Rs 5,000.
PAGE NO 14.21:
Question 19:
The difference between the compound interest and simple interest on a certain sum for 2 years at 7.5% per annum is Rs 360. Find the sum.
ANSWER:
Let the sum be P.
Thus, we have:CI − SI = 360
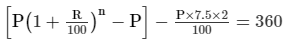
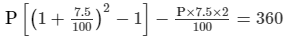
P[1.155625 − 1] − 0.15P = 3600.155625P − 0.15P = 3600.005625P = 360P = 360/0.005625P = 64000
Thus, the required sum is Rs 64,000.
PAGE NO 14.21:
Question 20:
The difference in simple interest and compound interest on a certain sum of money at 20/3% per annum for 3 years is Rs 46. Determine the sum.
ANSWER:
Given:CI − SI = 46
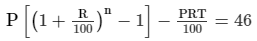
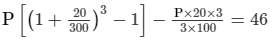
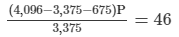
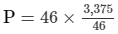
= 3,375
Thus, the required sum is Rs 3,375.
AGE NO 14.21:
Question 21:
Ishita invested a sum of Rs 12000 at 5% per annum compound interest. She received an amount of Rs 13230 after n years. Find the value of n.
ANSWER:
A = P(1 + R/100)n
13,230 = 12,000(1 + 5/100)n
(1.05)n = 13,230/12,000
(1.05)n = 1.1025
(1.05)n = (1.05)²
On comparing both the sides, we get:n = 2
Thus, the value of n is two years.
PAGE NO 14.21:
Question 22:
At what rate percent per annum will a sum of Rs 4000 yield compound interest of Rs 410 in 2 years?
ANSWER:
Let the rate percent be R.
We know that: CI = P(1 + R/100)n − P
410 = 4,000(1 + R/100)² − 4,000
4,410 = 4,000(1 + R/100)²
(1 + R/100)² = 4,410/4,000
(1 + R/100)² = 1.1025
(1 + R/100)² = (1.05)²
1 + R/100 = 1.05
R/100 = 0.05R = 5
Thus, the required rate percent is 5.
PAGE NO 14.21:
Question 23:
A sum of money deposited at 2% per annum compounded annually becomes Rs 10404 at the end of 2 years. Find the sum deposited.
ANSWER:
A = P(1 + R/100)n
10,404 = P(1 + 2100)²
10,404 = P(1.02)²
P = 10,404/1.0404
P = 10,000
Thus, the required sum is Rs 10,000.
PAGE NO 14.21:
Question 24:
In how much time will a sum of Rs 1600 amount to Rs 1852.20 at 5% per annum compound interest?
ANSWER:
A = P(1 + R/100)n
1852.20 = 1600(1 + 5/100)n
1852.20/1600 = (1.05)n
(1.05)n = 1.157625
(1.05)n = (1.05)³
On comparing both the sides, we get:n = 3
Thus, the required time is three years.
PAGE NO 14.21:
Question 25:
At what rate percent will a sum of Rs 1000 amount to Rs 1102.50 in 2 years at compound interest?
ANSWER:
A = P(1 + R/100)n
1102.50 = 1000(1 + R/100)²
1102.50/1000 = (1 + 0.01R)²
(1 + 0.01R)² = 1.1025
(1 + 0.01R)² = (1.05)²
On comparing both the sides, we get:1 + 0.01R = 1.05
0.01R = 0.05
R = 5
Thus, the required rate percent is 5.
PAGE NO 14.21:
Question 26:
The compound interest on Rs 1800 at 10% per annum for a certain period of time is Rs 378. Find the time in years.
ANSWER:
CI = P(1 + R/100)n − P
⇒ 378 = 1,800(1 + 10/100)n − 1,800
1,800(1 + 10/100)n = 2,178
(1 + 10/100)n = 2,178/1,800
(1.1)n = 1.21
(1.1)n = (1.1)²
On comparing both the sides, we get: n = 2
Thus, the required time is two years.
PAGE NO 14.21:
Question 27:
What sum of money will amount to Rs 45582.25 at 27/4% per annum in two years, interest being compounded annually?
ANSWER:
A = P(1 + R/100)n
45,582.25 = P(1 + 27/400)²
P(1.0675)² = 45,582.25
P = 45,582.25/1.13955625
P = 40,000
Thus, the required sum is Rs 40,000.
PAGE NO 14.21:
Question 28:
Sum of money amounts to Rs 453690 in 2 years at 6.5% per annum compounded annually. Find the sum.
ANSWER:
A = P(1 + R/100)n
453,690 = P(1 + 6.5/100)²
P(1.065)² = 453,690
P = 453,690/1.134225
P = 400,000
Thus, the required sum is Rs 400,000.
FAQs on Chapter 14 - Compound Interest (Part - 3), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is compound interest and how is it calculated? |  |
| 2. What is the difference between simple interest and compound interest? | |
| 3. How can I calculate the compound interest using the formula? | |
| 4. Can you provide an example of compound interest calculation? | |
| 5. Is there a simpler way to calculate compound interest without using the formula? | |
|
4.82/5 Rating |
|
Nov 22, 2024 Last updated |
|
Explore Courses for Class 8 exam
|
|
Semester Notes
,Chapter 14 - Compound Interest (Part - 3)
,Class 8
,Objective type Questions
,Free
,ppt
,shortcuts and tricks
,Class 8
,Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics
,Chapter 14 - Compound Interest (Part - 3)
,MCQs
,Extra Questions
,Viva Questions
,Important questions
,practice quizzes
,mock tests for examination
,Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics
,study material
,Previous Year Questions with Solutions
,Exam
,Chapter 14 - Compound Interest (Part - 3)
,past year papers
,Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics
,video lectures
,Sample Paper
,Class 8
,Summary
;
RD Sharma Solutions - Chapter 14 - Compound Interest (Part - 3), Class 8, Maths Free PDF Download
Importance of RD Sharma Solutions - Chapter 14 - Compound Interest (Part - 3), Class 8, Maths
RD Sharma Solutions - Chapter 14 - Compound Interest (Part - 3), Class 8, Maths Notes
RD Sharma Solutions - Chapter 14 - Compound Interest (Part - 3), Class 8, Maths Class 8 Questions
Study RD Sharma Solutions - Chapter 14 - Compound Interest (Part - 3), Class 8, Maths on the App
|
© EduRev
|
Education Revolution
|
Follow Us
|
