Chapter 14 - Compound Interest (Part - 2), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 14.14:
Question 1:
Compute the amount and the compound interest in each of the following by using the formulae when:
(i) Principal = Rs 3000, Rate = 5%, Time = 2 years
(ii) Principal = Rs 3000, Rate = 18%, Time = 2 years
(iii) Principal = Rs 5000, Rate = 10 paise per rupee per annum, Time = 2 years
(iv) Principal = Rs 2000, Rate = 4 paise per rupee per annum, Time = 3 years
(v) Principal = Rs 12800, Rate = 7(1/2)%, Time = 3 years
(vi) Principal = Rs 10000, Rate 20% per annum compounded half-yearly, Time = 2 years
(vii) Principal = Rs 160000, Rate = 10 paise per rupee per annum compounded half-yearly, Time = 2 years.
ANSWER:
Applying the rule A = P(1 + R/100)n on the given situations, we get:
(i)A = 3,000(1 + 5/100)²
= 3,000(1.05)²
= Rs 3,307.50
Now,CI = A − P
= Rs 3,307.50 − Rs 3,000
= Rs 307.50
(ii)A = 3,000(1 + 18/100)²
= 3,000(1.18)²
= Rs 4,177.20
Now,CI = A − P
= Rs 4,177.20 − Rs 3,000
= Rs 1,177.20
(iii)A = 5,000(1 + 10/100)²
= 5,000(1.10)²
= Rs 6,050
Now,CI = A − P
= Rs 6,050 − Rs 5,000
= Rs 1,050
(iv)A = 2,000(1 + 4/100)³
= 2,000(1.04)³
= Rs 2,249.68
Now,CI = A − P
= Rs 2,249.68 − Rs 2,000
= Rs 249.68
(v)A = 12,800(1 + 7.5/100)³
= 12,800(1.075)³
= Rs 15,901.40
Now,CI = A − P
= Rs 15,901.40 − Rs 12,800
= Rs 3,101.40
(vi)A = 10,000(1 + 20/200)4
= 10,000(1.1)4
= Rs 14,641
Now,CI = A − P
= Rs 14,641 − Rs 10,000
= Rs 4,641
(vii)A = 16,000(1 + 10/200)4
= 16,000(1.05)4
= Rs 19,448.1
Now,CI = A − P
= Rs 19,448.1 − Rs 16,000
= Rs 3,448.1
PAGE NO 14.14:
Question 2:
Find the amount of Rs 2400 after 3 years, when the interest is compounded annually at the rate of 20% per annum.
ANSWER:
Given: P = Rs 2,400
R = 20% p.a.
n = 3 years
We know that amount A at the end of n years at the rate R% per annum when the interest is compounded annually is given by
A = P(1 + R/100)n
∴ A = 2,400(1 + 20100)³
= 2,400(1.2)³
= 4,147.20
Thus, the required amount is Rs 4,147.20.
PAGE NO 14.14:
Question 3:
Rahman lent Rs 16000 to Rasheed at the rate of 12.5% per annum compound interest. Find the amount payable by Rasheed to Rahman after 3 years.
ANSWER:
Given: P = Rs 16,000
R = 12.5% p.a.
n = 3 years
We know that amount A at the end of n years at the rate R% per annum when the interest is compounded annually is given by
A = P(1 + R/100)n.
∴ A = 16,000(1 + 12.5/100)³
= 16,000(1.125)³
= 22,781.25
Thus, the required amount is Rs 22,781.25.
PAGE NO 14.14:
Question 4:
Meera borrowed a sum of Rs 1000 from Sita for two years. If the rate of interest is 10% compounded annually, find the amount that Meera has to pay back.
ANSWER:
Given: P = Rs 1,000
R = 10% p.a.
n = 2 years
We know that amount A at the end of n years at the rate R% per annum when the interest is compounded annually is given by
A = P(1 + R/100).
∴ A = 1,000(1 + 10/100)²
= 1,000(1.1)² = 1,210
Thus, the required amount is Rs 1,210.
PAGE NO 14.14:
Question 5:
Find the difference between the compound interest and simple interest. On a sum of Rs 50,000 at 10% per annum for 2 years.
ANSWER:
Given: P = Rs 50,000
R = 10% p.a.
n = 2 years
We know that amount A at the end of n years at the rate R% per annum when the interest is compounded annually is given by
A = P(1 + R/100)
.∴ A = Rs 50,000(1 + 10/100)²
= Rs 50,000(1.1)²
= Rs 60,500
Also,CI = A − P
= Rs 60,500 − Rs 50,000
= Rs 10,500
We know that:
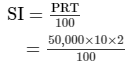
∴ Difference between CI and SI = Rs 10,500 − Rs 10,000
= Rs 500
PAGE NO 14.15:
Question 6:
Amit borrowed Rs 16000 at 17.5% per annum simple interest. On the same day, he lent it to Ashu at the same rate but compounded annually. What does he gain at the end of 2 years?
ANSWER:
Amount to be paid by Amit:
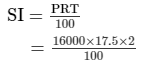
= Rs 5,600
Amount gained by Amit:A = P(1 + R/100)n
= Rs 16,000(1 + 17.5/100)²
= Rs 16,000(1.175)²
= Rs 22,090
We know that:CI = A − P
= Rs 22,090 − Rs 16,000 = Rs 6090
Amit's gain in the whole transaction = Rs 6,090 − Rs 5,600
= Rs 490
PAGE NO 14.15:
Question 7:
Find the amount of Rs 4096 for 18 months at 12.5% per annum, the interest being compounded semi-annually.
ANSWER:
Given:P = Rs 4,096
R = 12.5% p.a.
n = 18 months = 1.5 years
We have:A = P(1 + R/100)n
When the interest is compounded semi − annually, we have:
A = P(1 + R/200)²n
= Rs 4,096(1 + 12.5/200)³
= Rs 4,096(1.0625)³
= Rs 4,913
Thus, the required amount is Rs 4,913.
PAGE NO 14.15:
Question 8:
Find the amount and the compound interest on Rs 8000 for 1.5 years at 10% per annum, compounded half-yearly.
ANSWER:
Given: P = Rs 8,000
R = 10% p.a.
n = 1.5 years
When compounded half − yearly, we have:
A = P(1 + R/200)²n
= Rs 8,000(1 + 10/200)³
= Rs 8,000(1.05)³
= Rs 9,261
Also,CI = A − P
= Rs 9,261 − Rs 8,000
= Rs 1,261
PAGE NO 14.15:
Question 9:
Kamal borrowed Rs 57600 from LIC against her policy at 12.5% per annum to build a house. Find the amount that she pays to the LIC after 1.5 years if the interest is calculated half-yearly.
ANSWER:
Given: P = Rs 57,600
R = 12.5% p.a.
n = 1.5 years
When the interest is compounded half − yearly, we have:
A = P(1 + R/200)²n
= Rs 57,600(1 + 12.5/200)³
= Rs 57,600(1.0625)³
= Rs 69,089.06
Thus, the required amount is Rs 69,089.06.
PAGE NO 14.15:
Question 10:
Abha purchased a house from Avas Parishad on credit. If the cost of the house is Rs 64000 and the rate of interest is 5% per annum compounded half-yearly, find the interest paid by Abha after one year and a half.
ANSWER:
Given:P = Rs 64,000
R = 5% p.a.
n = 1.5 years
When the interest is compounded half − yearly, we have:
A = P(1 + R/200)²n
= Rs 64,000(1 + 5/200)³
= Rs 64,000(1.025)³
= Rs 68,921
Also,CI = A − P
= Rs 68,921 − Rs 64,000
= Rs 4,921
Thus, the required interest is Rs 4,921.
PAGE NO 14.15:
Question 11:
Rakesh lent out Rs 10000 for 2 years at 20% per annum, compounded annually. How much more he could earn if the interest be compounded half-yearly?
ANSWER:
Given:P = Rs 10,000
R = 20% p.a.
n = 2 years
A = P(1 + R/100)n
= Rs 10,000(1 + 20/100)²
= Rs 10,000(1.2)²
= Rs 14,400
When the interest is compounded half − yearly, we have:A = P(1 + R/200)²n
= Rs 10,000(1 + 20/200)4
= Rs 10,000(1.1)4
= Rs 14,641
Difference = Rs 14,641 − Rs 14,400
= Rs 241
PAGE NO 14.15:
Question 12:
Romesh borrowed a sum of Rs 245760 at 12.5% per annum, compounded annually. On the same day, he lent out his money to Ramu at the same rate of interest, but compounded semi-annually. Find his gain after 2 years.
ANSWER:
Given: P = Rs 245,760
R = 12.5% p.a.
n = 2 years
When compounded annually, we have:A = P(1 + R/100)n
= Rs 245,760(1 + 12.5/100)²
= Rs 311,040
When compounded semi − annually,
we have:A = P(1 + R/200)²n
= Rs 245,760(1 + 12.5/200)4
= Rs 245,760(1.0625)4
= Rs 313,203.75
Romesh's gain = Rs 313,203.75 − Rs 311,040
= Rs 2,163.75
PAGE NO 14.15:
Question 13:
Find the amount that David would receive if he invests Rs 8192 for 18 months at 12.5% per annum, the interest being compounded half-yearly.
ANSWER:
Given:P = Rs 8,192
R = 12.5% p.a.
n = 1.5 years
When the interest is compounded half − yearly, we have:A = P(1 + R/200)²n
= Rs 8,192(1 + 12.5/200)³
= Rs 8,192(1.0625)³
= Rs 9,826
Thus, the required amount is Rs 9,826.
PAGE NO 14.15:
Question 14:
Find the compound interest on Rs 15625 for 9 months, at 16% per annum, compounded quarterly.
ANSWER:
Given: P = Rs 15,625
R = 16% = 164 = 4% quarterly
n = 9 months = 3 quarters
We know that:A = P(1 + R/100)n
= Rs 15,625(1 + 4/100)³
= Rs 15,625(1.04)³
= Rs 17,576
Also,CI = A − P
= Rs 17,576 − Rs 15,625
= Rs 1,951
Thus, the required compound interest is Rs 1,951.
PAGE NO 14.15:
Question 15:
Rekha deposited Rs 16000 in a foreign bank which pays interest at the rate of 20% per annum compounded quarterly, find the interest received by Rekha after one year.
ANSWER:
Given:P = Rs 16,000
R = 20% p.a.
n = 1 year
We know that:A = P(1 + R/100)n
When compounded quarterly, we have:A = P(1 + R/400)4n
= Rs 16,000(1 + 20/400)4
= Rs 16,000(1.05)4
= Rs 19,448.10
Also,CI = A − P
= Rs 19,448.1 − Rs 16,000
= Rs 3,448.10
Thus, the interest received by Rekha after one year is Rs 3,448.10.
PAGE NO 14.15:
Question 16:
Find the amount of Rs 12500 for 2 years compounded annually, the rate of interest being 15% for the first year and 16% for the second year.
ANSWER:
Given: P = Rs 12,500
R1 = 15% p.a.
R2 = 16% p.a.
∴ Amount after two years = P(1 + R1/100)(1 + R2/100)
= Rs 12,500(1 + 15/100)(1 + 16/100)
= Rs 12,500(1.15)(1.16)
= Rs 16,675
Thus, the required amount is Rs 16,675.
PAGE NO 14.15:
Question 17:
Ramu borrowed Rs 15625 from a finance company to buy a scooter. If the rate of interest be 16% per annum compounded annually, what payment will he have to make after 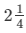 years?
years?
ANSWER:
Given: P = Rs 15,625
R = 16% p.a.
n = 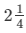 years
years
∴ Amount after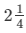 years = P
years = P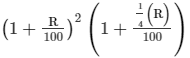
= Rs 15,625 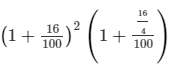
= Rs 15,625(1.16)²(1.04)
= Rs 21,866
Thus, the required amount is Rs 21,866.
PAGE NO 14.15:
Question 18:
What will Rs 125000 amount to at the rate of 6%, if the interest is calculated after every 3 months?
ANSWER:
Because interest is calculated after every 3 months, it is compounded quarterly.
Given:
P = Rs 125,000
R = 6% p.a. = 6/4% quarterly = 1.5% quarterly
n = 4
So,A = P(1 + R/100)n
= 125,000(1 + 1.5/100)4
= 125,000(1.015)4
= 132,670 (approx)
Thus, the required amount is Rs 132,670.
PAGE NO 14.15:
Question 19:
Find the compound interest at the rate of 5% for three years on that principal which in three years at the rate of 5% per annum gives Rs 12000 as simple interest.
ANSWER:
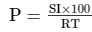
According to the given values, we have:
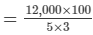
= 80,000
The principal is to be compounded annually.
So, A = P(1 + R/100)n
= 80,000(1 + 5/100)³
= 80,000(1.05)³
= 92,610
Now,CI = A − P
= 92,610 − 80,000
= 12,610
Thus, the required compound interest is Rs 12,610.
PAGE NO 14.15:
Question 20:
A sum of money was lent for 2 years at 20% compounded annually. If the interest is payable half-yearly instead of yearly, then the interest is Rs 482 more. Find the sum.
ANSWER:
A = P(1 + R/100)n
Also, P = A − CI
Let the sum of money be Rs x.
If the interest is compounded annually, then:
A1 = x(1 + 20/100)²
= 1.44x
∴ CI = 1.44x − x
= 0.44x ...(1)
If the interest is compounded half − yearly, then:
A2 = x(1 + 10/100)4
= 1.4641x
∴ CI = 1.4641x − x
= 0.4641x ...(2)
It is given that if interest is compounded half − yearly, then it will be Rs 482 more.
∴0.4641x = 0.44x + 482 [From (1) and (2)]
0.4641x − 0.44x = 482
0.0241x = 482
x = 482/0.0241
= 20,000
Thus, the required sum is Rs 20,000.
PAGE NO 14.15:
Question 21:
Simple interest on a sum of money for 2 years at 6.5% per annum is Rs 5200. What will be the compound interest on the sum at the same rate for the same period?
ANSWER:
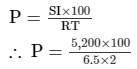
= 40,000
Now,
A = P(1 + R/100)n
= 40,000(1 + 6.5/100)²
= 40,000(1.065)²
= 45,369
Also,CI = A − P
= 45,369 − 40,000
= 5,369
Thus, the required compound interest is Rs 5,369
PAGE NO 14.15:
Question 22:
Find the compound interest at the rate of 5% per annum for 3 years on that principal which in 3 years at the rate of 5% per annum gives Rs 1200 as simple interest.
ANSWER:
We know that:
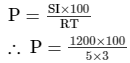
= 8,000
Now,
A = P(1 + R/100)n
= 8,000(1 + 5/100)³
= 8,000(1.05)³ = 9,261
Now,CI = A − P
= 9,261 − 8,000
= 1,261
Thus, the required compound interest is Rs 1,261.
FAQs on Chapter 14 - Compound Interest (Part - 2), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is compound interest? |  |
| 2. How is compound interest calculated? |  |
| 3. What is the difference between compound interest and simple interest? |  |
| 4. How can compound interest be beneficial? |  |
| 5. Can compound interest work against you? |  |


















