Chapter 16 - Understanding Shapes-II (Quadrilaterals), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 16.15:
Question 1:
Define the following terms:
(i) Quadrilateral
(ii) Convex Quadrilateral
ANSWER:
(i) A quadrilateral is a polygon that has four sides (or edges) and four vertices (or corners).
It can be any four-sided closed shape.
(ii) A convex quadrilateral is a mathematical figure whose every internal angle is less than or equal to 180 degrees.
Question 2:
In a quadrilateral, define each of the following:
(i) Sides
(ii) Vertices
(iii) Angles
(iv) Diagonals
(v) Adjacent angles
(vi) Adjacent sides
(vii) Opposite sides
(viii) Opposite angles
(ix) Interior
(x) Exterior
ANSWER:
(i) In a quadrilateral ABCD, the four line segments AB, BC, CD and DA are called its sides.(ii) The vertices of a quadrilateral are the corners of the quadrilateral. A quadrilateral has four vertices.
(iii) The meeting point of two sides of a quadrilateral is called an angle. A quadrilateral has four angles.
(iv) In a quadrilateral ABCD, the line segments AC and BD are called its diagonals.
(v) The angles which have a common side as their arm are called adjacent angles.
(vi) Two sides are adjacent if they have a common end point.
(vii) Two sides are opposite if they do not have a common end point.
(viii) The two angles of a quadrilateral which are not adjacent are called opposite angles.(ix) The part of the plane made up by all such points that are enclosed by quadrilateral is called the interior.
(x) The part of the plane made up by all the points that are not enclosed by quadrilateral is called the exterior.
Question 3:
Complete each of the following, so as to make a true statement:
(i) A quadrilateral has ....... sides.
(ii) A quadrilateral has ...... angles.
(iii) A quadrilateral has ..... vertices, no three of which are .....
(iv) A quadrilateral has .... diagonals.
(v) The number of pairs of adjacent angles of a quadrilateral is .......
(vi) The number of pairs of opposite angles of a quadrilateral is .......
(vii) The sum of the angles of a quadrilateral is ......
(viii) A diagonal of a quadrilateral is a line segment that joins two ...... vertices of the quadrilateral.
(ix) The sum of the angles of a quadrilateral is .... right angles.
(x) The measure of each angle of a convex quadrilateral is ..... 180°.
(xi) In a quadrilateral the point of intersection of the diagonals lies in .... of the quadrilateral.
(xii) A point is in the interior of a convex quadrilateral, if it is in the ..... of its two opposite angles.
(xiii) A quadrilateral is convex if for each side, the remaining .... lie on the same side of the line containing the side.
ANSWER:
(i) four
(ii) four
(iii) four, collinear
(iv) two
(v) four
(vi) two
(vii) 360°
(viii) opposite
(ix) four
(x) less than
(xi) the interior
(xii) interiors
(xiii) vertices
PAGE NO 16.16:
Question 4:
In Fig. 16.19, ABCD is a quadrilateral.
(i) Name a pair of adjacent sides.
(ii) Name a pair of opposite sides.
(iii) How many pairs of adjacent sides are there?
(iv) How many pairs of opposite sides are there?
(v) Name a pair of adjacent angles.
(vi) Name a pair of opposite angles.
(vii) How many pairs of adjacent angles are there?
(viii) How many pairs of opposite angles are there?
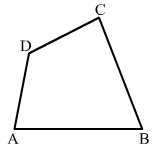
ANSWER:
(i) (AB, BC) or (BC, CD) or (CD, DA) or (AD, AB)
(ii) (AB, CD) or (BC, DA)
(iii) Four(iv) Two
(v) (∠A, ∠B) or (∠B, ∠C) or (∠C, ∠D) or (∠D, ∠A)
(vi) (∠A, ∠C) or (∠B, ∠D)
(vii) Four
(viii) Two
Question 5:
The angles of a quadrilateral are 110°, 72°, 55° and x°. Find the value of x.
ANSWER:
The sum of angles of a quadrilateral is 360°.
So, we get 110° + 72° + 55° + x = 360°
⇒ 237° + x = 360°
⇒ x = 360°−237°
∴ x = 123°
Question 6:
The three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
ANSWER:
Let x be the the fourth angle.
Since, the sum of all the angles of a quadrilateral is 360°,
we have:110° + 50° + 40° + x = 360°
⇒ 200° + x = 360°
⇒ x = 160°
∴ The fourth angle is 160°.
Question 7:
A quadrilateral has three acute angles each measures 80°. What is the measure of the fourth angle?
ANSWER:
Let x be the fourth angle.Since, the sum of all angles of a quadrilateral is 360°,
we have:80° + 80° + 80° + x = 360°
⇒ 240° + x = 360°
⇒ x = 120°
∴ The fourth angle is 120°.
Question 8:
A quadrilateral has all its four angles of the same measure. What is the measure of each?
ANSWER:
Let x be the measure of each angle.Since, the sum of all the angles of a quadrilateral is 360°,
we have:x° + x° + x° + x° = 360°
⇒ 4x° = 360°
⇒ x° = 90°
∴ The measure of each angle is 90°.
Question 9:
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles?
ANSWER:
Let x be the measure of each angle.
Since, the sum of all the angles of a quadrilateral is 360°,
we have:65° + 65° + x° + x° = 360°
⇒ 2x° + 130° = 360°
⇒ 2x° = 230°
⇒ x° = 115°
∴ The measure of each angle is 115°.
Question 10:
Three angles of a quadrilateral are equal. Fourth angle is of measure 150°. What is the measure of equal angles.
ANSWER:
Let x be the measure of the equal angles of the quadrilateral.Since, the sum of all the angles of a quadrilateral is 360°,
we have:x° + x° + x° + 150° = 360°
⇒ 3x° = 360°−150°
⇒ x° = 210°
∴ The measure of each angle is 70°.
Question 11:
The four angles of a quadrilateral are as 3 : 5 : 7 : 9. Find the angles.
ANSWER:
Let the angles be in the ratio 3x : 5x : 7x : 9x.
Since, the sum of all the angles of a quadrilateral is 360°,
we have:3x + 5x + 7x + 9x = 360°
⇒ 24x = 360°
⇒ x = 15°
Thus, the angles are:3x = 45°
5x = 75°7x = 105°
9x = 135°
Question 12:
If the sum of the two angles of a quadrilateral is 180°. What is the sum of the remaining two angles?
ANSWER:
Let (x + y) be the sum of the remaining two angles.Since, the sum of all the angles of a quadrilateral is 360°,
we have:180° + (x + y)° = 360°
⇒ (x + y)° = 180°
∴ The sum of the remaining two angles is 180°.
Question 13:
In Fig. 16.20, find the measure of ∠MPN.
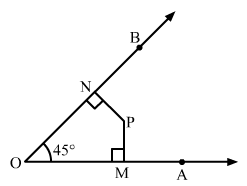
ANSWER:
Since the sum of all the angles of a quadrilateral is 360°, we have:45° + 90° + 90° + ∠MPN = 360°
⇒ 225° + ∠MPN = 360°
∴ ∠MPN = 135°
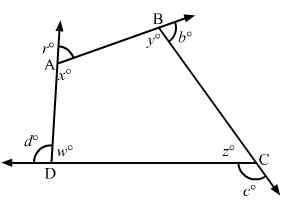
Question 14:
The sides of a quadrilateral are produced in order. What is the sum of the four exterior angles?
ANSWER:
The sides of the quadrilateral ABCD are produced in order (according to figure).
Now, we need to find the sum of the exterior angles.Since the angles made on the same side of straight line are 180°,
i.e., linear pair, we have:a + x + b + y + c + z + w + d
= 180° + 180° + 180° + 180°
= 720°
OR Sum of the interior angles + sum of exterior the angles = 180° × 4 = 720°
Since the sum of the interior angles of a quadrilateral is 360°,
we have:
w + x + y + z = 360°
Substituting the value, we get:a + b + c + d = 360°
∴ Sum of the exterior angles = 360°
Question 15:
In Fig. 16.21, the bisectors of ∠A and ∠B meet at a point P. If ∠C = 100° and ∠D = 50°, find the measure of ∠APB.
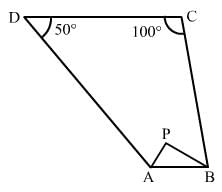
ANSWER:
∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠A + ∠B + 100° + 50° = 360°
⇒ ∠A + ∠B = 210° ...(i)
In △APB, we have:
1/2∠A + 1/2∠B + ∠APB = 180°
⇒ ∠APB = 180°−1/2(∠A + ∠B)
From (i), we get:
⇒ ∠APB = 180°−(1/2 × 210°)
∴∠APB = 75°
PAGE NO 16.17:
Question 16:
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angle of the quadrilateral.
ANSWER:
Let x be the measure of each angle.Then the ratio becomes x : 2x : 4x : 5x.
Since, the sum of all angles in a quadrilateral is 360°,
we have:x + 2x + 4x + 5x = 360°
⇒ 12x = 360°
⇒ x = 360°/12
⇒ x = 30°
Thus, the angles are:
x = 30°
2x = 60°
4x = 120°
5x = 150°
Question 17:
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD = 12(∠A + ∠B).∠COD = 12(∠A + ∠B).
ANSWER:
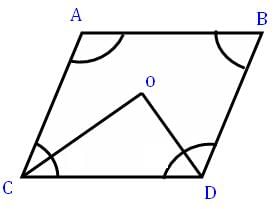
∠COD = 180°−(∠OCD + ∠ODC)
= 180°−1/2(∠C + ∠D)
= 180°−1/2[360°−(∠A + ∠B)]
= 180°−180° + 1/2(∠A + ∠B)
= 1/2(∠A + ∠B) = RHS
Hence proved.
Question 18:
Find the number of sides of a regular polygon, when each of its angles has a measure of
(i) 160°
(ii) 135°
(iii) 175°
(iv) 162°
(v) 150°
ANSWER:
(i) Each interior angle =
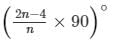
So, 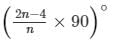 = 160°
= 160°
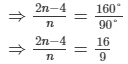
⇒ 18n−36 = 16n
⇒ 2n = 36
∴ n = 18
(ii) Each interior angle = 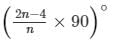
So,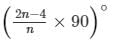 = 135°
= 135°
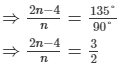
⇒ 4n−8 = 3n
∴ n = 8
(iii) Each interior angle = 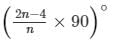
So, 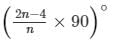 = 175°
= 175°
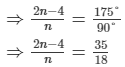
⇒ 36n−72 = 35n
∴ n = 72
(iv) Each interior angle = 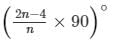
So, 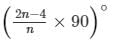 = 162°
= 162°
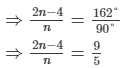
⇒ 10n−20 = 9n
∴ n = 20
(v) Each interior angle =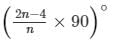
So, 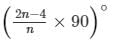 = 150°
= 150°
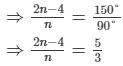
⇒ 6n−12 = 5n
∴ n = 12
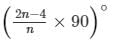
Question 19:
Find the number of degrees in each exterior exterior angle of a regular pentagon.
ANSWER:
Each exterior angle = (360/n)°
For a regular pentagon, n = 5.
∴ Exterior angle = (360/5)° = 72°
Question 20:
The measure of angles of a hexagon are x°, (x − 5)°, (x − 5)°, (2x − 5)°, (2x − 5)°, (2x + 20)°.
Find the value of x.
ANSWER:
Since the sum of all the angles of a hexagon is 720°,
we get:
x° + (x−5)° + (x−5)° + (2x−5)° + (2x−5)° + (2x + 20)° = 720°
⇒ x° + x°−5° + x°−5° + 2x−5° + 2x−5° + 2x + 20° = 720°
⇒ 9x−20° + 20° = 720°
⇒ 9x = 720°
∴ x = 80
Question 21:
In a convex hexagon, prove that the sum of all interior angle is equal to twice the sum of its exterior angles formed by producing the sides in the same order.
ANSWER:
For a convex hexagon, interior angle = 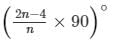
For a hexagon, n = 6
∴ Interior angle = (12−4/6 × 90°) = (86 × 90°) = 120°
So, the sum of all the interior angles = 120° + 120° + 120° + 120° + 120° + 120° = 720°
∴ Exterior angle = (360/n)° = (360/6)° = 60°
So, sum of all the exterior angles = 60° + 60° + 60° + 60° + 60° + 60° = 360°
Now, sum of all interior angles = 720° = 2
(360°) = twice the exterior angles
Hence proved.
Question 22:
The sum of the interior angles of a polygon is three times the sum of its exterior angles. Determine the number of sided of the polygon.
ANSWER:
{(2n−4) × 90°} = 3 × (360°/n × n)
⇒ (n−2) × 180 = 3 × 360
⇒ n−2 = 6∴ n = 8
Question 23:
Determine the number of sides of a polygon whose exterior and interior angles are in the ratio 1 : 5.
ANSWER:
Let n be the number of sides of a polygon.
Let x and 5x be the exterior and interior angles.
Since the sum of an interior and the corresponding exterior angle is 180°,
we have:x + 5x = 180°
⇒ 6x = 180°
⇒ x = 30°
The polygon has n sides. So, sum of all the exterior angles = (30n)°
We know that the sum of all the exterior angles of a polygon is 360°.
i.e., 30n = 360
∴ n = 12
Question 24:
PQRSTU is a regular hexagon. Determine each angle of ΔPQT.
ANSWER:
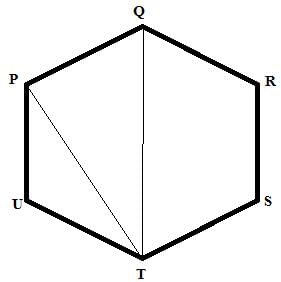
A regular hexagon is made up of 6 equilateral triangles.
So, ∠PQT = 60° and ∠QTP = 30°
Since the sum of the angles of ΔPQT is 180°,
we have:∠P + ∠Q + ∠T = 180°
⇒ ∠P + 60° + 30° = 180°
⇒ ∠P = 180°−90°
⇒ ∠QPT = 90°
∴ The angles of the triangle are 90°, 60° and 30°.


















