Chapter 17 - Understanding Shapes-III (Part - 2), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 17.16:
Question 1:
Which of the following statements are true for a rhombus?
(i) It has two pairs of parallel sides.
(ii) It has two pairs of equal sides.
(iii) It has only two pairs of equal sides.
(iv) Two of its angles are at right angles.
(v) Its diagonals bisect each other at right angles.
(vi) Its diagonals are equal and perpendicular.
(vii) It has all its sides of equal lengths.
(viii) It is a parallelogram.
(ix) It is a quadrilateral.
(x) It can be a square.
(xi) It is a square.
ANSWER:
(i) True
(ii) True
(iii) True
(iv) False
(v) True
(vi) False
Diagonals of a rhombus are perpendicular, but not equal.
(vii) True
(viii) True
It is a parallelogram because it has two pairs of parallel sides.
(ix) True
It is a quadrilateral because it has four sides.
(x) True
It can be a square if each of the angle is a right angle.
(xi) False
It is not a square because each of the angle is a right angle in a square.
PAGE NO 17.17:
Question 2:
Fill in the blanks, in each of the following, so as to make the statement true:
(i) A rhombus is a parallelogram in which ......
(ii) A square is a rhombus in which ......
(iii) A rhombus has all its sides of ...... length.
(iv) The diagonals of a rhombus ...... each other at ...... angles.
(v) If the diagonals of a parallelogram bisect each other at right angles, then it is a ......
ANSWER:
(i) A rhombus is a parallelogram in which adjacent sides are equal.
(ii) A square is a rhombus in which all angles are right angled.
(iii) A rhombus has all its sides of equal length.
(iv) The diagonals of a rhombus bisect each other at right angles.
(v) If the diagonals of a parallelogram bisect each other at right angles, then it is a rhombus.
Question 3:
The diagonals of a parallelogram are not perpendicular. Is it a rhombus? Why or why not?
ANSWER:
No, it is not a rhombus. This is because diagonals of a rhombus must be perpendicular.
Question 4:
The diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? If your answer is 'No', draw a figure to justify your answer.
ANSWER:
No, it is not so.
Diagonals of a rhombus are perpendicular and bisect each other. Along with this, all of its sides are equal. In the figure given below, the diagonals are perpendicular to each other, but do not bisect each other.
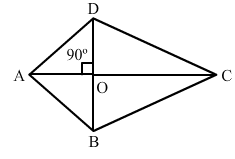
Question 5:
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
ANSWER:
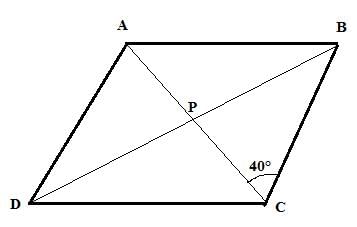
In a rhombus, the diagonals are perpendicular.
∴ ∠BPC = 90°
From Δ BPC, the sum of angles is 180°.
∴ ∠CBP + ∠BPC + ∠PBC = 180°
∠CBP = 180°−∠BPC−∠PBC
∠CBP = 180°−40°−90° = 50°
∠ADB = ∠CBP = 50° (alternate angle)
Question 6:
If the diagonals of a rhombus are 12 cm and 16cm, find the length of each side.
ANSWER:
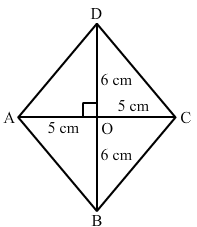
All sides of a rhombus are equal in length.The diagonals intersect at 90° and the sides of the rhombus form right triangles.
One leg of these right triangles is equal to 8 cm and the other is equal to 6 cm.
The sides of the triangle form the hypotenuse of these right triangles.
So, we get:(82 + 62)cm² = (64 + 36)cm² = 100 cm²
The hypotneuse is the square root of 100cm².
This makes the hypotneuse equal to 10.
Thus, the side of the rhombus is equal to 10 cm.
Question 7:
Construct a rhombus whose diagonals are of length 10 cm and 6 cm.
ANSWER:
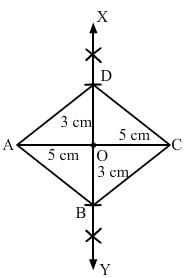
1. Draw AC equal to 10 cm.
2. Draw XY, the right bisector of AC, meeting it at O.
3. With O as centre and radius equal to half of the length of the other diagonal,
i.e. 3 cm, cut OB = OD = 3 cm.
4. Join AB, AD and CB, CD.
Question 8:
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
ANSWER:
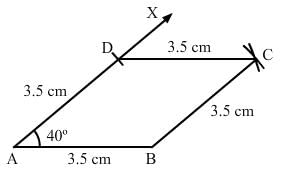
1. Draw a line segment AB of 3.5 cm.
2. Draw ∠BAX equal to 40°.
3. With A as centre and the radius equal to AB, cut AD at 3.5 cm.
4. With D as centre, cut an arc of radius 3.5 cm.
5. With B as centre, cut an arc of radius 3.5 cm. This arc cuts the arc of step 4 at C.
6. Join DC and BC.
Question 9:
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
ANSWER:
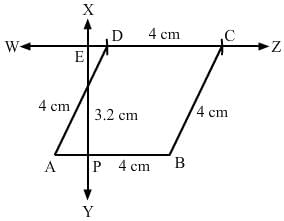
1. Draw a line segment AB of 4 cm.
2. Draw a perpendicular XY on AB, which intersects AB at P.
3. With P as centre, cut PE at 3.2 cm.
4. Draw a line WZ that passes through E. This line should be parallel to AB.
5. With A as centre, draw an arc of radius 4 cm that cuts WZ at D.
6. With D as centre and radius 4 cm, cut line DZ. Label it as point C.
4. Join AD and CB.
Question 10:
Draw a rhombus ABCD, if AB = 6 cm and AC = 5 cm.
ANSWER:
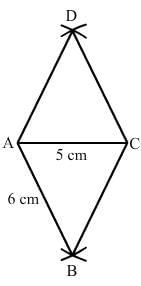
1. Draw a line segment AC of 5 cm.
2. With A as centre, draw an arc of radius 6 cm on each side of AC.
3. With C as centre, draw an arc of radius 6 cm on each side of AC. These arcs intersect the arcs of step 2 at B and D.
4. Join AB, AD, CD and CB.
Question 11:
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
ANSWER:
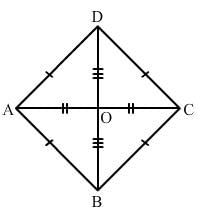
(i) Yes
In ΔBCO and ΔDCO:
OC = OC (common)
BC = DC (all sides of a rhombus are equal)
BO = OD (diagonals of a rhomus bisect each other)
By SSS congruence:ΔBCO ≅ ΔDCO
(ii) Yes
By c.p.c.t:
∠BCO = ∠DCO
Question 12:
Show that each diagonal of a rhombus bisects the angle through which it passes.
ANSWER:
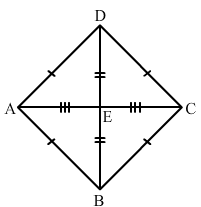
In ΔAED and ΔDEC:
AE = EC (diagonals bisect each other)
AD = DC (sides are equal)
DE = DE (common)
By SSS congruence: ΔAED≅ ΔCED
∠ADE = ∠CDE (c.p.c.t)
Similarly, we can prove ΔAEB and ΔBEC, ΔBEC and ΔDEC, ΔAED and ΔAEB are congruent to each other.
Hence, diagonal of a rhombus bisects the angle through which it passes.
Question 13:
ABCD is a rhombus whose diagonals intersect at O. If AB = 10 cm, diagonal BD = 16 cm, find the length of diagonal AC.
ANSWER:
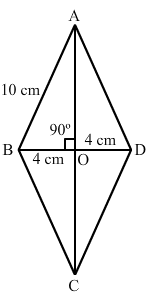
We know that the diagonals of a rhombus bisect each other at right angles.
∴ BO = 1/2 BD = (1/2×16) cm = 8cm
AB = 10 cm and
∠AOB = 90°
From right ΔOAB: AB2 = AO2 + BO2
⇒ AO2 = (AB2–BO2)
⇒ AO2 = (10)2−(8)2cm²
⇒ AO2 = (100−64) cm²
= 36cm²
⇒ AO = 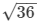 cm = 6cm
cm = 6cm
∴ AC = 2×AO = (2×6) cm = 12 cm
Question 14:
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm.
If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral?
ANSWER:
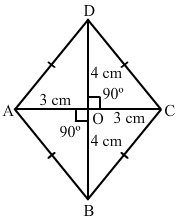
Let the given quadrilateral be ABCD in which diagonals AC is equal to 6 cm and BD is equal to 8 cm.
Also, it is given that the diagonals bisect each other at right angle, at point O.
∴ AO = OC = 1/2AC = 3 cm
Also, OB = OD = 1/2BD = 4 cm
In right △AOB:AB2 = OA2 + OB2
⇒ AB2 = (9 + 16) cm²
⇒ AB2 = 25 cm²
⇒ AB = 5 cmThus, the length of each side of the quadrilateral is 5 cm.
FAQs on Chapter 17 - Understanding Shapes-III (Part - 2), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What are the different types of shapes covered in Chapter 17 of RD Sharma Class 8 Maths? |  |
| 2. How can I identify the properties of different shapes? |  |
| 3. What are some important theorems related to shapes covered in Chapter 17? |  |
| 4. How can I calculate the area and perimeter of different shapes? |  |
| 5. How can I apply the concepts of shapes in real-life situations? |  |





















