Chapter 17 - Understanding Shapes-III (Part - 3), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 17.22:
Question 1:
Which of the following statements are true for a rectangle?
(i) It has two pairs of equal sides.
(ii) It has all its sides of equal length.
(iii) Its diagonals are equal.
(iv) Its diagonals bisect each other.
(v) Its diagonals are perpendicular.
(vi) Its diagonals are perpendicular and bisect each other.
(vii) Its diagonals are equal and bisect each other.
(viii) Its diagonals are equal and perpendicular, and bisect each other.
(ix) All rectangles are squares.
(x) All rhombuses are parallelograms.
(xi) All squares are rhombuses and also rectangles.
(xii) All squares are not parallelograms.
ANSWER:
(i) True
(ii) False
(iii) True
(iv) True
(v) False
(vi) False
The diagonals are not perpendicular to each other.
(vii) True
(viii) False
The diagonals are not perpendicular to each other.
(ix) False
All sides are not equal.
(x) True
(xi) True
(xii) False
All squares are parallelogram.
Question 2:
Which of the following statements are true for a square?
(i) It is a rectangle.
(ii) It has all its sides of equal length.
(iii) Its diagonals bisect each other at right angle.
(iv) Its diagonals are equal to its sides.
ANSWER:
(i) True
(ii) True
(iii) True
(iv) False
This is because the hypotenuse in any right angle triangle is always greater than its two sides.
PAGE NO 17.23:
Question 3:
Fill in the blanks in each of the following, so as to make the statement true:
(i) A rectangle is a parallelogram in which .....
(ii) A square is a rhombus in which .....
(iii) A square is a rectangle in which .....
ANSWER:
(i) A rectangle is a parallelogram in which each angle is a right angle.
(ii) A square is a rhombus in which each angle is a right angle.
(iii) A square is a rectangle in which the adjacent sides are equal.
Question 4:
A window frame has one diagonal longer than the other. Is the window frame a rectangle? Why or why not?
ANSWER:
No, since diagonals of a rectangle are equal.
Question 5:
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
ANSWER:
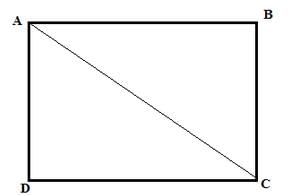
In ∆ACB and ∆CAD:
AB = CD (rectangle property)
AD = BC (rectangle property)
AC ( common side )
Hence, by SSS criterion, it is proved that ΔACB ≅ ΔCAD
Question 6:
The sides of a rectangle are in the ratio 2 : 3, and its perimeter is 20 cm. Draw the rectangle.
ANSWER:
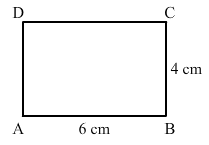
Let the side be x cm and y cm.
So, we have: 2(x + y) = 20
Sides are in the ratio 2:3.
∴ y = 3x/2
Putting the value of y:
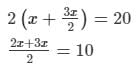
5x = 20
x = 4
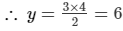
Thus, sides of the rectangle will be 4 cm and 6 cm.
ABCD is the rectangle having sides 4 cm and 6 cm.
Question 7:
The sides of a rectangle are in the ratio 4 : 5. Find its sides if the perimeter is 90 cm.
ANSWER:
Let the side be x cm and y cm.
So, we have: 2(x + y) = 90
Sides are in the ratio 4:5.
∴ y = 5x/4
Putting the value of y:
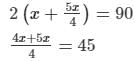
x = 180
x = 20
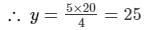
Thus, the sides of the rectangle will be 20 cm and 25 cm.
Question 8:
Find the length of the diagonal of a rectangle whose sides are 12 cm and 5 cm.
ANSWER:
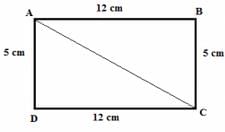
Using Pythagoras theorem:AD2 + DC2 = AC2
52 + 122 = AC2
25 + 14 = AC2
169 = AC2
AC = 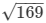 = 13 cm
= 13 cm
Thus, length of the diagonal is 13 cm.
Question 9:
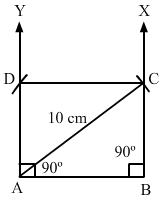
Draw a rectangle whose one side measures 8 cm and the length of each of whose diagonals is 10 cm.
ANSWER:
(i) Draw a side AB, equal to 8 cm.
(ii) With A as the centre, draw an arc of length 10 cm.
(iii) Draw ∠ABX = 90°, which intersects the arc at C.
(iv)Draw ∠BAY = 90°.
(v) With C as the centre, draw an arc of length 8 cm.
(vi) Join CD.
Thus, ABCD is the required rectangle.
Question 10:
Draw a square whose each side measures 4.8 cm.
ANSWER:
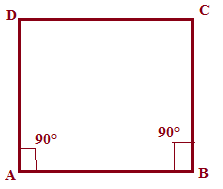
(i) Draw side AB = 4.8 cm.
(ii) From A, make an angle of 90° and cut it at 4.8 cm and mark it point D.
(iii) From B, make an angle of 90° and cut it at 4.8 cm and mark it point C.
(iv) Join C and D.Thus, ABCD is the required square.
Question 11:
Identify all the quadrilaterals that have:
(i) Four sides of equal length
(ii) Four right angles
ANSWER:
(i) If all four sides are equal, then it can be either a square or a rhombus.
(ii) All four right angles, make it either a rectangle or a square.
Question 12:
Explain how a square is
(i) a quadrilateral?
(ii) a parallelogram?
(iii) a rhombus?
(iv) a rectangle?
ANSWER:
(i) Since a square has four sides, it is a quadrilateral.
(ii) Since the opposite sides are parallel and equal, it is a parallelogram.
(iii) Since the diagonals bisect each other and all the sides are equal, it is a rhombus.
(iv) Since the opposite sides are equal and all the angles are right angles, it is a rectangle.
Question 13:
Name the quadrilaterals whose diagonals:
(i) bisect each other
(ii) are perpendicular bisector of each other
(iii) are equal.
ANSWER:
(i) Rhombus, parallelogram, rectangle and square
(ii) Rhombus and square
(iii) Rectangle and square
Question 14:
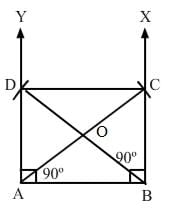
ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C.
ANSWER:
(i) Construct a triangle ABC right angle at B.
(ii) Suppose O is the mid point of AC.(iii)Complete the rectangle ABCD having AC as its diagonal.
Since diagonals of a rectangle are equal and they bisect each other, O is the midpoint of both AC and BD.
∴ OA = OB = OC
Question 15:
A mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
ANSWER:
(i) By measuring each angle - Each angle of a rectangle is 90°°.
(ii) By measuring the length of the diagonals - Diagonals of a rectangle are equal.
(iii) By measuring the sides of rectangle - Each pair of opposite sides are equal.
FAQs on Chapter 17 - Understanding Shapes-III (Part - 3), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What are the properties of a rectangle? |  |
| 2. How can we find the area of a triangle? |  |
| 3. What is the difference between a square and a rhombus? |  |
| 4. Can a parallelogram have four right angles? |  |
| 5. How can we determine if a quadrilateral is a trapezium? |  |

|
Explore Courses for Class 8 exam
|

|

















