Chapter 18 - Practical Geometry (Constructions) (Part - 5), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 18.8:
Question 1:
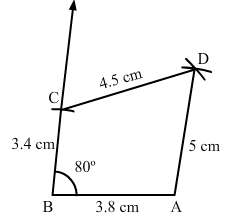
Construct a quadrilateral ABCD in which AB = 3.8 cm, BC = 3.4 cm, CD = 4.5 cm, AD = 5 cm and ∠B = 80°.
ANSWER:
Steps of construction:
Step I: Draw AB = 3.8 cm.
Step II: Construct ∠ABC = 80°.
Step III : With B as the centre and radius 3.4 cm, cut off BC = 3.4 cm.
Step IV: With C as the centre and radius 4.5 cm, draw an arc.
Step V :With A as the centre and radius 5.3 cm, draw an arc to intersect the arc drawn in Step IV at D.
Step VI: Join AD, BC and CD to obtained the required quadrilateral.
Question 2:
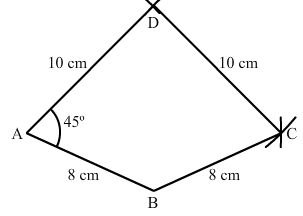
Construct a quadrilateral ABCD, given that AB = 8 cm, BC = 8 cm, CD = 10 cm, AD = 10 cm and ∠A = 45°.
ANSWER:
Steps of Construction:
Step I: Draw AB = 8 cm.
Step II: Construct ∠BAD = 45°.
Step III : With A as the centre and radius 10 cm, cut off AD = 10 cm.
Step IV: With D as the centre and radius 10 cm, draw an arc.
Step V :With B as the centre and radius 8 cm, draw an arc to intersect the arc drawn in Step IV at C.
Step VI: Join BC and CD to obtained the required quadrilateral.
Question 3:
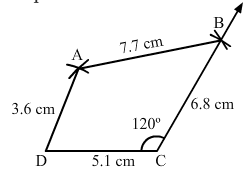
Construct a quadrilateral ABCD in which AB = 7.7 cm, BC = 6.8 cm, CD = 5.1 cm, AD = 3.6 cm and ∠C = 120°.
ANSWER:
Steps of construction:
Step I: Draw DC = 5.1 cm.
Step II: Construct ∠DCB = 120°.
Step III : With C as the centre and radius 6.8 cm, cut off BC = 6.8 cm.
Step IV: With B as the centre and radius 7.7 cm, draw an arc.
Step V :With D as the centre and radius 3.6 cm, draw an arc to intersect the arc drawn in Step IV at A.
Step VI: Join AB and AD to obtained the required quadrilateral.
Question 4:
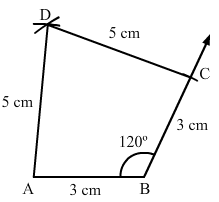
Construct a quadrilateral ABCD in which AB = BC = 3 cm, AD = CD = 5 cm, and ∠B = 120°.
ANSWER:
Steps of construction:
Step I: Draw AB = 3 cm.
Step II: Construct ∠ABC = 120°.
Step III : With B as the centre and radius 3 cm, cut off BC = 3 cm.
Step IV: With C as the centre and radius 5 cm, draw an arc.
Step V :With A as the centre and radius 5 cm, draw an arc to intersect the arc drawn in Step IV at D.
Step VI: Join AD and CD to obtained the required quadrilateral.
Question 5:
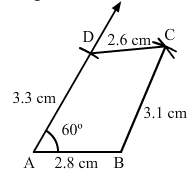
Construct a quadrilateral ABCD in which AB = 2.8 cm, BC = 3.1 cm, CD = 2.6 cm, and DA = 3.3 cm and ∠A = 60°.
ANSWER:
Steps of construction:
Step I: Draw AB = 2.8 cm.
Step II: Construct ∠BAD = 60°.
Step III : With A as the centre and radius 3.3 cm, cut off AD = 3.3 cm.
Step IV: With D as the centre and radius 2.6 cm, draw an arc.
Step V :With B as the centre and radius 3.1 cm, draw an arc to intersect the arc drawn in Step IV at C.
Step VI: Join BC and CD to obtained the required quadrilateral.
Question 6:
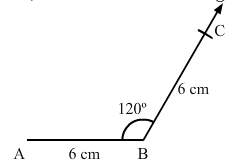
Construct a quadrilateral ABCD in which AB = BC = 6 cm, AD = DC = 4.5 cm and ∠B = 120°.
ANSWER:
Steps of construction:
Step I: Draw AB = 6 cm.
Step II: Construct ∠ABC = 120°.
Step III : With B as the centre and radius 6 cm, cut off BC = 6 cm.
Now, we can see that AC is about 10.3 cm
which is greater than AD+CD = 4.5+4.5 = 9 cm.
We know that sum of the lengths of two sides of triangle is always greater than the third side but here, the sum of AD and CD is less than AC.
So, construction of the given quadrilateral is not possible.
FAQs on Chapter 18 - Practical Geometry (Constructions) (Part - 5), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. How do I construct a perpendicular bisector of a line segment? |  |
| 2. Can we construct a triangle with any three given line segments? |  |
| 3. How do I construct an angle bisector? |  |
| 4. How do I construct a triangle given its three sides? |  |
| 5. How do I construct a line parallel to a given line through a given point? |  |





















