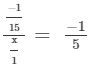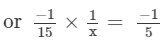Chapter 2 - Powers (Ex-2.1) - Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Express each of the following as a rational number of the form p/q, where p and q are integers and q ≠ 0.
(i) 2−3
(ii) (−4)−2
(iii) 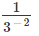
(iv)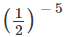
(v)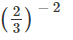
Answer 1: We know that a − n =
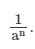 Therefore,
Therefore,
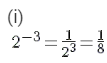
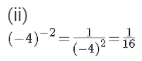
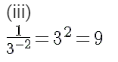
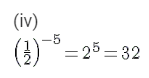
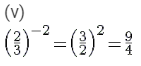
Question 2: Fiind the value of each of the following:
(i) 3−1 + 4−1
(ii) (30 + 4−1) × 22
(iii) (3−1 + 4−1 + 5−1)0
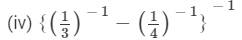
Answer 2:
(i) We know from the property of powers that for every natural number a, a−1 = 1/a. Then:
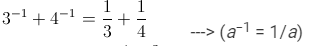
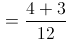
= 7/12
(ii) We know from the property of powers that for every natural number a, a−1 = 1/a.
Moreover, a0 is 1 for every natural number a not equal to 0. Then:
(30+4−1)×22
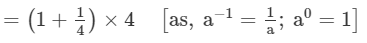
=5/4 ×4
= 5
(iii) We know from the property of powers that for every natural number a, a−1 = 1/a.
Moreover, a0 is 1 for every natural number a not equal to 0. Then:
(3−1+4−1+5−1)=1 ---> (Ignore the expression inside the bracket and use a0 = 1 immediately.)
(iv) We know from the property of powers that for every natural number a, a−1 = 1/a. Then:
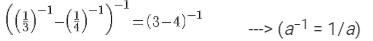
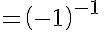
=−1 ---> (a−1 = 1/a)
Question 3:Find the value of each of the following:
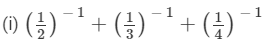
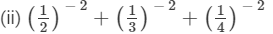
(iii) (2−1 × 4−1) ÷ 2−2
(iv) (5−1 × 2−1) ÷ 6−1
Answer 3:
(i)
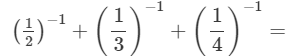
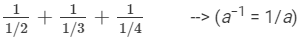
(ii)
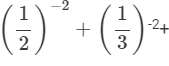 14-2=11/22+11/32+11/42 --> (a−n = 1/(an))
14-2=11/22+11/32+11/42 --> (a−n = 1/(an)) 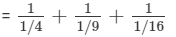 --> ((a/b)n = (an/bn))
--> ((a/b)n = (an/bn))
= 4+9+16
=29
(iii)
(2−1×4−1)÷2−2= 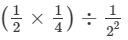 --> (a−n = 1/(an))
--> (a−n = 1/(an))
=1/8×4
= 2
(iv)
(5−1×2−1)÷6−1= 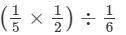 --> (a−n = 1/(an))
--> (a−n = 1/(an))
= 1/10 × 6
= 3/5
Question 4: Simplify:
(i) (4−1×3−1)2
(ii) (5−1÷6−1)3
(iii) (2−1+3−1)−1
(iv) (3−1×4−1)−1×5−1
Answer 4: (i)
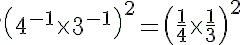 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
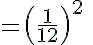
(ii)
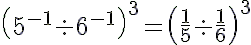 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
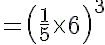
= (6/5)3
= (6)3 /(5)3 ---> ((a/b)n = (an)/(bn) )
= 216/125
(iii)
(2−1+3−1)−1 =(12+13)−1 ---> (a−1 = 1/a)
= (56)−1
=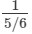 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
=6/5
(iv)
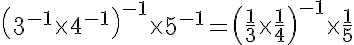 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
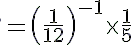
= 12/5 ---> (a−1 = 1/a)
Question 5: Simplify:
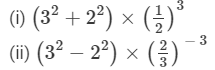
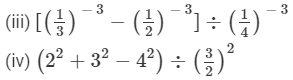
Answer 5:
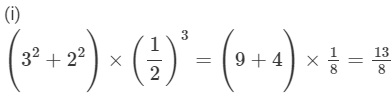
(ii)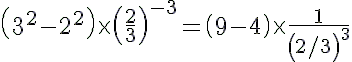 ---> (a−1=1/(an))
---> (a−1=1/(an))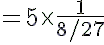 ---> ((a/b)n = (an)/(bn))
---> ((a/b)n = (an)/(bn))
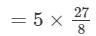
= 135/8
(iii)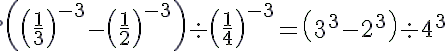 --->(a-n = 1/(an))
--->(a-n = 1/(an))
= (27−8)÷64
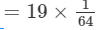
= 19/64
(iv)
(22+32−42)÷(32)2=(4+9−16)× 9/4 ---> ((a/b)n = (an)/(bn))
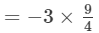
= -27/4
Question 6: By what number should 5−1 be multiplied so that the product may be equal to (−7)−1?
Answer 6: Using the property a−1 = 1/a for every natural number a, we have 5−1 = 1/5 and (−7)−1 = −1/7. We have to find a number x such that
1/5 ×x= -1/7
Multiplying both sides by 5, we get:
x= -5/7
Hence, the required number is −5/7.
Question 7: By what number should 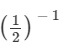
be multiplied so that the product may be equal to 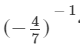
?
Answer 7: Using the property a−1 = 1/a for every natural number a, we have (1/2)−1 = 2 and (−4/7)−1 = −7/4. We have to find a number x such that
2x= -7/4Dividing both sides by 2, we get:
x=-7/8
Hence, the required number is −7/8.
Question 8: By what number should (−15)−1 be divided so that the quotient may be equal to (−5)−1?
Answer 8: Using the property a−1 = 1/a for every natural number a, we have (−15)−1 = −1/15 and (−5)−1 = −1/5. We have to find a number x such that
or x = 1/3
Hence, (−15)−1 should be divided by 1/3 to obtain (−5)−1.
Question 9: Write each of the following in exponential form:
(i) (3/2)−1×(3/2)−1×(3/2)−1×(3/2)−1
(ii) (2/5)−2×(2/5)−2×(2/5)−2
Answer 9:
(i) (3/2)−1×(3/2)−1×(3/2)−1×(3/2)−1=(3/2)−1+(−1)+(−1)+(−1) {am×an=am+n}Question 10: Evaluate:
(i) 5−2
(ii) (−3)−2
(iii) (1/3)−4
(iv) (- 1/2)−1
Answer 10:
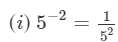 ---> (a−n = 1/(an))
---> (a−n = 1/(an))
= 1/25
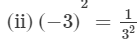 ---> (a−n = 1/(an))
---> (a−n = 1/(an))
= 1/9
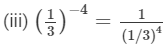 ---> (a−n = 1/(an))
---> (a−n = 1/(an))
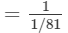
= 81
(iv) 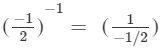 ---> (a−1 = 1/(a))
---> (a−1 = 1/(a))
= -2
Question 11: Express each of the following as a rational number in the form p/q:
(i) 6−1
(ii) (−7)−1
(iii) (1/4)−1
(iv) (-4) -1 × (-3/2) -1
(v) (3/5) -1 ×( 5/2) -1
Answer 11:
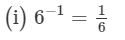 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
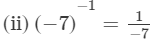 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
= -1/7
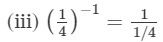 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
= 4
(iv) 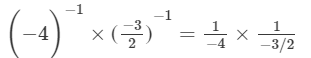 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
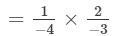
= 1/6
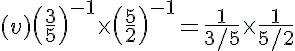 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
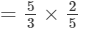
= 2/3
Question 12: Simplify:
(i) {4−1×3−1}2
(ii) {5−1÷6−1}3
(iii) (2−1+3−1)−1
(iv) {3−1×4−1}−1×5−1
(v) (4−1−5−1)÷3−1
Answer 12:
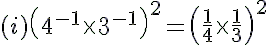 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
= (1/12) 2
=(1)2/(12)2 --->((a/b)n = (an)/(bn))
= 1/144
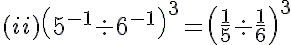 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
= ( 6/5) 3
= 216/125 --->((a/b)n = (an)/(bn))
(iii) (2−1 + 3−1)−1 = 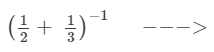 −−−> (a−1= 1/a)
−−−> (a−1= 1/a)
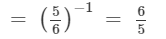 −−−> (a−1= 1/a)
−−−> (a−1= 1/a)
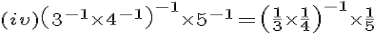 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
=(1/12)−1 × 1/5
=12×1/5 ---> (a−1 = 1/a)
= 12/5
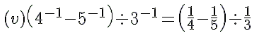 ---> (a−1 = 1/a)
---> (a−1 = 1/a)
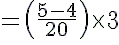
=1/20 ×3
= 3/20
Question 13: Express each of the following rational numbers with a negative exponent:
(i) (1/4)3
(ii) 35
(iii) (3/5)4
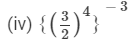
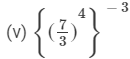
Answer 13:
(i). (1/4)3
=(4/1)−3 [∵ a−n = 1 / an]
(ii). (3)5
=(1/3)−5 [∵ a−n =1 / an]
(iii) (3/5)4
=(5/3)−4 [∵ a−n =1 / an]
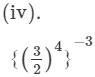
=(3/2)−12 [∵ (am)n = amn]
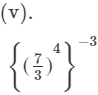
=(7/3)−12 [∵ (am)n = amn]
FAQs on Chapter 2 - Powers (Ex-2.1) - Class 8 Math RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What are powers in mathematics? |  |
| 2. How do you read powers? |  |
| 3. What is the value of a number raised to the power of 0? |  |
| 4. How do you multiply numbers with the same base but different exponents? |  |
| 5. How do you divide numbers with the same base but different exponents? |  |