Chapter 23 - Data Handling-I (Part - 1), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 23.7:
Question 1:
Define the following terms:
(i) Observations
(ii) Raw data
(iii) Frequency of an observation
(iv) Frequency distribution
(v) Discrete frequency distribution
(vi) Grouped frequency distribution
(vii) Class-interval
(viii) Class-size
(ix) Class limits
(x) True class limits
ANSWER:
(i) Observation is the value at a particular period of a particular variable.
(ii) Raw data is the data collected in its original form.
(iii) Frequency of an observation is the number of times a certain value or a class of values occurs.
(iv) Frequency distribution is the organisation of raw data in table form with classes and frequencies.
(v) Discrete frequency distribution is a frequency distribution where sufficiently great numbers are grouped into one class.
(vi) Grouped frequency distribution is a frequency distribution where several numbers are grouped into one class.
(vii) Class interval is the width of such a class.
(viii) Class size is the difference between the upper and the lower values of a class.
(ix) Class limits are the smallest and the largest observations (data, events, etc.) in a class.
(x) True class limits are the actual class limits of a class.
Question 2:
The final marks in mathematics of 30 students are as follows:
| 53, | 61, | 48, | 60, | 78, | 68, | 55, | 100, | 67, | 90, | 75, | 88, | 77, | 37, | 84, |
| 58, | 60, | 48, | 62, | 56, | 44, | 58, | 52, | 64, | 98, | 59, | 70, | 39, | 50, | 60 |
(i) Arrange these marks in the ascending order, 30 to 39 one group, 40 to 49 second group etc.
Now answer the following:
(ii) What is the highest score?
(iii) What is the lowest score?
(iv) What is the range?
(v) If 40 is the pass mark how many have failed?
(vi) How many have scored 75 or more?
(vii) Which observations between 50 and 60 have not actually appeared?
(viii) How many have scored less than 50?
ANSWER:
The given raw data can be arranged in an ascending order. The class intervals are 30 − 39, 40 − 49,...100 − 109. Then, take the raw data and place it in the appropriate class intervals.
(i) The marks can be arranged in an ascending order as shown below:
30 to 39 → 37, 39
40 to 49 → 44, 48, 48
50 to 59 → 50, 52, 53,
55, 56, 58, 58, 59
60 to 69 → 60, 60, 60, 61, 62, 64, 67, 68
70 to 79 → 70, 75, 77, 78
80 to 89 → 84, 88
90 to 99 → 90, 98
100 to 109 → 100
(ii) The highest score is 100.
(iii) The lowest score is 37.
(iv) The range is 100 − 37, i.e. 63.
(v) If 40 is the passing mark, then the number of students who failed is 2 (i.e. 37, 39).
(vi) The number of students scoring 75 and above is 8 (i.e. 75, 77, 78, 84, 88, 90, 98, 100).
(vii) The marks 51, 54, and 57 do not actually appear between 50 and 60.
(viii) The number of students scoring less than 50 is 5 (i.e. 37, 39, 44, 48, 48).
Question 3:
The weights of new born babies (in kg) in a hospital on a particular day are as follows:
2.3, 2.2, 2.1, 2.7, 2.6, 3.0, 2.5, 2.9, 2.8, 3.1, 2.5, 2.8, 2.7, 2.9, 2.4
(i) Rearrange the weights in descending order.
(ii) Determine the highest weight.
(iii) Determine the lowest weight.
(iv) Determine the range.
(v) How many babies were born on that day?
(vi) How many babies weigh below 2.5 kg?
(vii) How many babies weigh more than 2.8 kg?
(viii) How many babies weigh 2.8 kg?
ANSWER:
The frequency distribution of the weights of new born babies in a hospital on a particular day is represented in the following table:
(i) The weights of the newly born babies in descending order are as follows:
| Weight | Tally marks | Frequency |
| 3.1 | I | 1 |
| 3.0 | I | 1 |
| 2.9 | II | 2 |
| 2.8 | II | 2 |
| 2.7 | II | 2 |
| 2.6 | I | 1 |
| 2.5 | II | 2 |
| 2.4 | I | 1 |
| 2.3 | I | 1 |
| 2.2 | I | 1 |
| 2.1 | I | 1 |
(ii) The highest weight is 3.1 kg.
(iii) The lowest weight is 2.1 kg.
(iv) The range is 3.1 − 2.1, i.e. 1 kg.
(v) The number of babies born on that day is 15.
(vi) The number of babies whose weights are below 2.5 kg is 4 (i.e. 2.4, 2.3, 2.2, 2.1).
(vii) The number of babies whose weights are more than 2.8 kg is 4 (i.e. 3.1, 3.0, 2.9, 2.9).
(viii) The number of babies whose weight is 2.8 kg is 2.
PAGE NO 23.8:
Question 4:
Following data gives the number of children in 40 families:
1, 2, 6, 5, 1, 5, 1, 3, 2, 6, 2, 3, 4, 2, 0, 0, 4, 4, 3, 2, 2, 0, 0, 1, 2, 2, 4, 3, 2, 1, 0, 5, 1, 2, 4, 3, 4, 1, 6, 2, 2.
Represent it in the form of a frequency distribution.
ANSWER:
The data can be put in the form of frequency distribution in the following manner:
| Number of Children | Tally marks | Frequency |
| 0 | 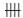 | 5 |
| 1 | 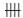 || || | 7 |
| 2 | 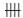 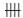 || || | 12 |
| 3 | 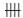 | 5 |
| 4 | 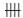 | | | 6 |
| 5 | ||| | 3 |
| 6 | ||| | 3 |
Question 5:
Prepare a frequency table of the following scores obtained by 50 students in a test:
| 42, | 51, | 21, | 42, | 37, | 37, | 42, | 49, | 38, | 52, | 7, | 33, | 17, |
| 44, | 39, | 7, | 14, | 27, | 39, | 42, | 42, | 62, | 37, | 39, | 67, | 51, |
| 53, | 53, | 59, | 41, | 29, | 38, | 27, | 31, | 64, | 19, | 53, | 51, | 22, |
| 61, | 42, | 39, | 59, | 47, | 33, | 34, | 16, | 37, | 57, | 43, |
ANSWER:
The frequency table of 50 students is given below:
| Marks | Number of Students | Marks | Number of Students | Marks | Number of Students |
| 7 | 2 | 33 | 2 | 49 | 1 |
| 14 | 1 | 34 | 1 | 51 | 3 |
| 16 | 1 | 37 | 4 | 52 | 1 |
| 17 | 1 | 38 | 2 | 53 | 3 |
| 19 | 1 | 39 | 4 | 54 | 1 |
| 21 | 1 | 41 | 1 | 57 | 1 |
| 22 | 1 | 42 | 6 | 59 | 2 |
| 27 | 2 | 43 | 1 | 61 | 1 |
| 29 | 1 | 44 | 1 | 62 | 1 |
| 31 | 1 | 47 | 1 | 67 | 1 |
Question 6:
A die was thrown 25 times and following scores were obtained:
| 1, | 5, | 2, | 4, | 3, | 6, | 1, | 4, | 2, | 5, | 1, | 6, | 2, |
| 6, | 3, | 5, | 4, | 1, | 3, | 2, | 3, | 6, | 1, | 5, | 2, |
Prepare a frequency table of the scores.
ANSWER:
The frequency of the scores of the die is shown below:
| The Die | Tally Marks | Frequency |
| 1 | 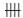 | 5 |
| 2 | 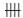 | 5 |
| 3 | |||| | 4 |
| 4 | ||| | 3 |
| 5 | |||| | 4 |
| 6 | |||| | 4 |
Question 7:
In a study of number of accidents per day, the observations for 30 days were obtained as follows:
| 6, | 3, | 5, | 6, | 4, | 3, | 2, | 5, | 4, | 2, | 4, | 2, | 1, | 2, | 2, |
| 0, | 5, | 4, | 6, | 1, | 6, | 0, | 5, | 3, | 6, | 1, | 5, | 5, | 2, | 6 |
Prepare a frequency distribution table.
ANSWER:
The frequency table for the number of accidents per day for a period of 30 days is given below:
| Number of Accidents | Tally Marks | Frequency |
| 0 | || | 2 |
| 1 | ||| | 3 |
| 2 | 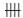 | | | 6 |
| 3 | ||| | 3 |
| 4 | |||| | 4 |
| 5 | 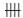 | | | 6 |
| 6 | 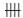 | | | 6 |
Question 8:
Prepare a frequency table of the following ages (in years) of 30 students of class VIII in your school:
13, 14, 13, 12, 14, 13, 14, 15, 13, 14, 13, 14, 16, 12, 14, 13, 14, 15, 16, 13, 14, 13, 12, 17, 13, 12, 13, 13, 13, 14
ANSWER:
The frequency table of the ages of 30 students of class VII in the school is given below:
| Age | Tally Marks | Frequency |
| 12 | |||| | 4 |
| 13 | 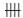 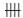 || || | 12 |
| 14 | 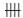 |||| |||| | 9 |
| 15 | || | 2 |
| 16 | || | 2 |
| 17 | | | 1 |
Question 9:
Following figures relate to the weekly wages (in Rs) of 15 workers in a factory:
300, 250, 200, 250, 200, 150, 350, 200, 250, 200, 150, 300, 150, 200, 250
Prepare a frequency table.
(i) What is the range in wages (in Rs)?
(ii) How many workers are getting Rs 350?
(iii) How many workers are getting the minimum wages?
ANSWER:
The frequency table for the number of accidents per day for a period of 30 days is given below:
| Wage (in Rs) | Tally Marks | Frequency |
| 150 | ||| | 3 |
| 200 | 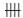 | 5 |
| 250 | |||| | 4 |
| 300 | || | 2 |
| 350 | | | 1 |
(i) The range of wages (in Rs) is 350 − 150 i.e. 200.
(ii) From the frequency table, we can see that the number of workers earning Rs 350 is 1.
(iii) Here, the minimum wage is 150. Hence, the number of workers earning the minimum wage is 3.
Question 10:
Construct a frequency distribution table for the following marks obtained by 25 students in a history test in class VIII of a school:
9, 17, 12, 20, 9, 18, 25, 17, 19, 9, 12, 9, 12, 18, 17, 19, 20, 25, 9, 12, 17, 19, 19, 20, 9
(i) What is the range of marks?
(ii) What is the highest mark?
(iii) Which mark is occurring more frequently?
ANSWER:
The frequency distribution table is given below:
| Age | Tally marks | Frequency |
| 9 | 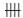 | | | 6 |
| 12 | |||| | 4 |
| 17 | |||| | 4 |
| 18 | || | 2 |
| 19 | |||| | 4 |
| 20 | ||| | 3 |
| 25 | || | 2 |
(i) The range of marks is 25 − 9, i.e. 16.
(ii) The highest mark is 25.
(iii) The mark that occurs most frequently is 9. It occurs 6 times.
FAQs on Chapter 23 - Data Handling-I (Part - 1), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the importance of data handling in mathematics? |  |
| 2. What are the different types of data representation methods? |  |
| 3. How can I collect data for a statistical analysis? |  |
| 4. What is the difference between qualitative and quantitative data? |  |
| 5. How can I interpret data from a bar graph? |  |





















