Chapter 25 - Data Handling-III (Part - 1), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 25.12:
Question 1:
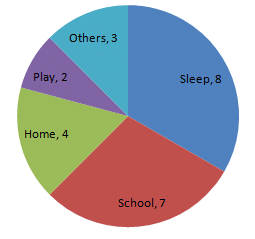
The number of hours, spent by a school boy on different activities in a working day, is given below:
| Activities | Sleep | School | Home | Play | Others | Total |
| Number of hours | 8 | 7 | 4 | 2 | 3 | 24 |
Present the information in the form of a pie-chart.
Ans.
We know:
Central angle of a component = (component value / sum of component values × 360)
Here, total number of hours = 24
Thus, the central angle for each component can be calculated as follows:
| Activity | Number of hours | Sector angle |
| Sleep | 8 | 8/24 × 360 = 120o |
| School | 7 | 7/24 × 360 = 105o |
| Home | 4 | 4/24 × 360 = 60o |
| Play | 2 | 2/24 × 360 = 30o |
| Others | 3 | 3/24 × 360 = 45o |
Now, the pie chat that represents the given data can be constructed by following the steps given below:
Step 1 : Draw a circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here, the largest central angle is 120o. Draw a sector with the central angle 120o in such a way that one of its radii coincides with the radius drawn in step 2 and another radius is in its counter-clockwise direction.
Step 4 : Construct other sectors representing other items in the clockwise direction in descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them as shown as in the figure below.
PAGE NO 25.12:
Question 2:
Employees of a company have been categorized according to their religions as given below:
| Religions | Hindu | Muslim | Sikh | Christian | Total |
| Number of workers | 420 | 300 | 225 | 105 | 1080 |
Draw a pie-chart to represent the above information.
Ans.
We know:
Central angle of a component = (component value / sum of component values × 360ο)
Here, total number of workers = 1050
Thus, the central angle for each component can be calculated as follows:
| Religion | Number of workers | Sector angle |
| Hindu | 420 | 420/1050 × 360 = 144 |
| Muslim | 300 | 300/1050 × 360 = 102.9 |
| Sikh | 225 | 225/1050 × 360 = 77.14 |
| Christian | 105 | 105/1050 × 360 = 36 |
Note: The total number of workers is 1050, not 1080.
Now, the pie chat that represents the given data can be constructed by following the steps below:
Step 1 : Draw circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here, the largest central angle is 144o. Draw a sector with the central angle 144o in such a way that one of its radii coincides with the radius drawn in step 2 and another radius is in its counter clockwise direction.
Step 4 : Construct other sectors representing other items in the clockwise direction in the descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them as shown as in the figure below.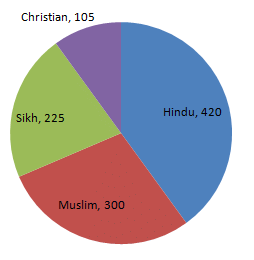
PAGE NO 25.12:
Question 3:
In one day the sales (in rupees) of different items of a baker's shop are given below:
| Items | Ordinary bread | Fruit bread | Cakes and Pastries | Biscuits | Others | Total |
| Sales (in Rs) | 260 | 40 | 100 | 60 | 20 | 480 |
Draw a pie-chart representing the above sales.
Ans.
We know:
Central angle of a component = (component value/sum of component values × 360)
Here, total sales = Rs 480
Thus, the central angle for each component can be calculated as follows:
| Item | Sale (in Rs) | Sector angle |
| Ordinary bread | 260 | 260/480 × 360 = 195 |
| Fruit bread | 40 | 40/480 × 360 = 30 |
| Cakes and pastries | 100 | 100/480 × 360 = 75 |
| Biscuits | 60 | 60/480 × 360 = 45 |
| Others | 20 | 20/480 × 360 = 15 |
Now, the pie chat representing the given data can be constructed by following the steps below:
Step 1 : Draw circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here, the largest central angle is 195o. Draw a sector with the central angle 195o in such a way that one of its radii coincides with the radius drawn in step 2 and another radius is in its counter clockwise direction.
Step 4 : Construct other sectors representing other items in the clockwise direction in the descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them, as shown as in the figure below.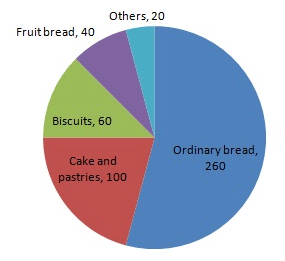
PAGE NO 25.12:
Question 4:
The following data shows the expenditure of a person on different items during a month. Represent the data by a pie-chart.
| Items of expenditure | Rent | Education | Food | Clothing | Others |
| Amount (in Rs) | 2700 | 1800 | 2400 | 1500 | 2400 |
Ans.
We know:
Central angle of a component = (component value/sum of component values × 360)
Here, total amount = Rs 10800
Thus, the central angle for each component can be calculated as follows:
| Item | Amount (in Rs) | Sector angle |
| Rent | 2700 | 2700/10800 × 360 = 90 |
| Education | 1800 | 1800/10800 × 360 = 60 |
| Food | 2400 | 2400/10800 × 360 = 80 |
| Clothing | 1500 | 1500/10800 × 360 = 50 |
| Others | 2400 | 2400/10800 × 360 = 80 |
Total : 10800 (in Rs)
Now, the pie chat representing the given data can be constructed by following the steps below:
Step 1 : Draw circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here, the largest central angle is 90o. Draw a sector with the central angle 90oin such a way that one radius coincides with the radius drawn in step 2 and another radius is in its counter clockwise direction.
Step 4 : Construct other sectors representing other items in the clockwise direction in descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them, as shown as in the figure below.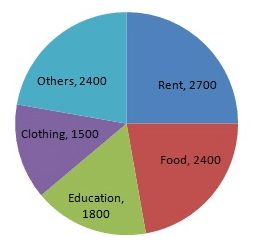
PAGE NO 25.12:
Question 5:
The percentages of various categories of workers in a state are given in the following table.
| Categoies | Culti-vators | Agricultural Labourers | Industrial Workers | Commercial Workers | Others |
| % of workers | 40 | 25 | 12.5 | 10 | 12.5 |
Present the information in the form a pie-chart.
Ans.
We know:
Central angle of a component = (component value/sum of component values × 360)
Here, total percentage of workers = 100
Thus, the central angle for each component can be calculated as follows:
| Category | Percentage of workers | Sector angle |
| Cultivators | 40 | 40/100 × 360 = 144 |
| Agricultural labourers | 25 | 25/100 × 360 = 90 |
| Industrial workers | 12.5 | 12.5/100 × 360 = 45 |
| Commercial workers | 10 | 10/100 × 360 = 36 |
| Others | 12.5 | 12.5/100 × 360 = 45 |
Now, the pie chat representing the given data can be constructed by following the steps below:
Step 1 : Draw circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here, the largest central angle is 144o. Draw a sector with the central angle 144o in such a way that one of its radii coincides with the radius drawn in step 2 and another radius is in its counter clockwise direction.
Step 4 : Construct other sectors representing other items in the clockwise direction in descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them, as shown as in figure below.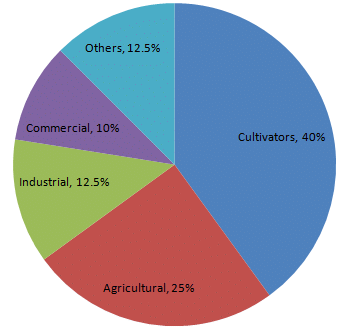
PAGE NO 25.12:
Question 6:
The following table shows the expenditure incurred by a publisher in publishing a book:
| Items | Paper | Printing | Binding | Advertising | Miscellaneous |
| Expenditure (in%) | 35% | 20% | 10% | 5% | 30% |
Present the above data in the form of a pie-chart.
Ans.
We know:
Central angle of a component = (component value/sum of component values × 360)
Here the total % of expenditures = 100%
Thus the central angle for each component can be calculated as follows:
| Item | Expenditure (in %) | Sector angle |
| Paper | 35 | 35/100 × 360 = 126 |
| Printing | 20 | 20/100 × 360 = 72 |
| Binding | 10 | 10/100 × 360 = 36 |
| Advertising | 5 | 5/100 × 360 = 18 |
| Miscellaneous | 30 | 30/100 × 360 = 108 |
Now, the pie chat representing the given data can be constructed by following the steps below:
Step 1 : Draw circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here, the largest central angle is 126o. Draw a sector with the central angle 126o in such a way that one of its radii coincides with the radius drawn in step 2 and another radius is in its counter clockwise direction.
Step 4 : Construct other sectors representing other items in the clockwise direction in descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them, as shown as in figure below.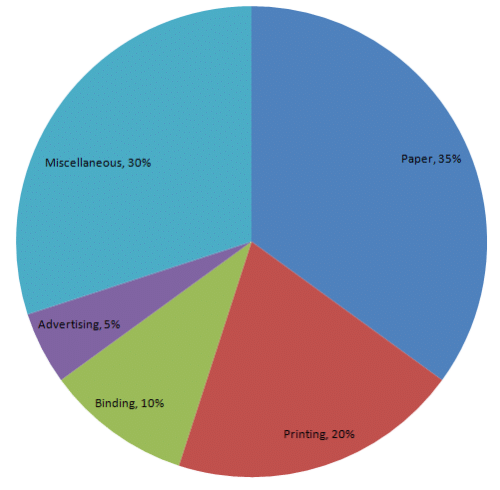
PAGE NO 25.12:
Question 7:
Percentage of the different products of a village in a particular district are given below. Draw a pie-chart representing this information.
| Items | Wheat | Pulses | Jwar | Grounnuts | Vegetables | Total |
| % | 12531253 | 12561256 | 252252 | 503503 | 253253 | 100 |
Ans.
We know:
Central angle of a component = (component value/sum of component values × 360ο)
Here, the total % of items = 100
Thus, the central angle for each component can be calculated as follows:
| Item | In % | Sector angle | |
| Wheat | 125/3 | 41.66 | 41.66/100 × 360 = 149.97 |
| Pulses | 125/6 | 20.83 | 20.83/100 × 360 = 74.98 |
| Jwar | 25/2 | 12.5 | 12.5/100 × 360 = 45 |
| Groundnuts | 50/3 | 16.66 | 16.66/100 × 360 = 59.97 |
| Vegetables | 25/3 | 8.33 | 8.33/100 × 360 = 29.98 |
Now, the pie chat representing the given data can be constructed by following the steps below:
Step 1 : Draw circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here the largest central angle is 149.97o. Draw a sector with the central angle 149.97o in such a way that one of its radii coincides with the radius drawn in step 2 and another radius is in its counter clockwise direction.
Step 4 : Construct other sectors representing other items in the clockwise sense in descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them, as shown as in the figure below.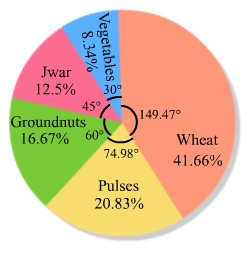
PAGE NO 25.13:
Question 8:
Draw a pie-diagram for the following data of expenditure pattern in a family:
| Items | Food | Clothing | Rent | Education | Unforeseen events | Midicine |
| Expenditure (in percent) | 40% | 20% | 10% | 10% | 15% | 5% |
Ans.
We know:
Central angle of a component = (component value/sum of component values × 360ο)
Here, the total % of items = 100
Thus, central angle for each component can be calculated as follows:
| Item | Expenditure | Sector angle |
| Food | 40% | 40/100 × 360 = 144 |
| Clothing | 20% | 20/100 × 360 = 72 |
| Rent | 10% | 10/100 × 360 = 36 |
| Education | 10% | 10/100 × 360 = 36 |
| Unforeseen events | 15% | 15/100 × 360 = 54 |
| Medicine | 5% | 5/100 × 360 = 18 |
Now, the pie chat representing the given data can be constructed by following the steps below:
Step 1 : Draw circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here the largest central angle is 144o. Draw a sector with the central angle 144o in such a way that one of its radii coincides with the radius drawn in step 2 and another radius is in its counter clockwise direction.
Step 4 : Construct other sectors representing other items in the clockwise sense in descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them, as shown as in figure below.
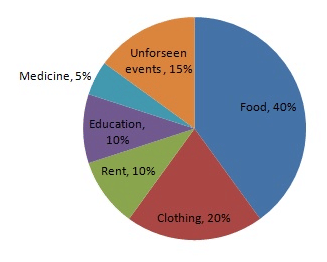
PAGE NO 25.13:
Question 9:
Draw a pie-diagram of the areas of continents of the world given in the following table:
| Continents | Asia | U.S.S.R | Africa | Europe | Noth America | South America | Australia |
| Area (in million sq. km) | 26.9 | 20.5 | 30.3 | 4.9 | 24.3 | 17.9 | 8.5 |
Ans.
We know:
Central angle of a component = (component value/sum of component values × 360)
Here, total area in million sq km = 133.3
Thus, the central angle for each component can be calculated as follows:
| Continent | Area (in million sq. km) | Sector angle |
| Asia | 26.9 | 26.9/133.3 × 360 = 72.6 |
| U.S.S.R | 20.5 | 20.5/133.3 × 360 = 55.4 |
| Africa | 30.3 | 30.3/133.3 × 360 = 81.8 |
| Europe | 4.9 | 4.9/133.3 × 360 = 13.2 |
| North America | 24.3 | 24.3/133.3 × 360 = 65.6 |
| South America | 17.9 | 17.9/133.3 × 360 = 48.3 |
| Australia | 8.5 | 8.5/133.3 × 360 = 23 |
Now, the pie chat representing the given data can be constructed by following the steps below:
Step 1 : Draw circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here the largest central angle is 81.8o. Draw a sector with the central angle 81.8o in such a way that one of its radii coincides with the radius drawn in step 2 and another radius is in its counter clockwise direction.
Step 4 : Construct other sectors representing other items in the clockwise sense in descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them, as shown as in figure below.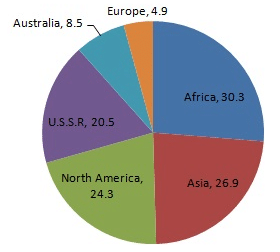
PAGE NO 25.13:
Question 10:
The following data gives the amount spent on the construction of a house. Draw a pie diagram.
| Items | Cement | Timber | Bricks | Labour | Steel | Miscellaneous |
| Expenditure (in thousand Rs) | 60 | 30 | 45 | 75 | 45 | 45 |
Ans.
We know:
Central angle of a component = (component value/sum of component values × 360)
Here. the total expenditures = 300 (in thousand Rs)
Thus the central angle for each component can be calculated as follows:
| Item | Expenditure (in thousand Rs) | Sector angle |
| Cement | 60 | 60/300 × 360 = 72 |
| Timber | 30 | 30/300 × 360 = 36 |
| Bricks | 45 | 45/300 × 360 = 54 |
| Labour | 75 | 75/300 × 360 = 90 |
| Steel | 45 | 45/300 × 360 = 54 |
| Miscellaneous | 45 | 45/300 × 360 = 54 |
Total expenditure: 300 (in thousand Rs)
Now, the pie chat representing the given data can be constructed by following the steps below:
Step 1 : Draw circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here the largest central angle is 90o. Draw a sector with the central angle 90oin such a way that one of its radii coincides with the radius drawn in step 2 and another radius is in its counter clockwise direction.
Step 4 : Construct other sectors representing the other items in the clockwise direction in descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them, as shown as in figure below.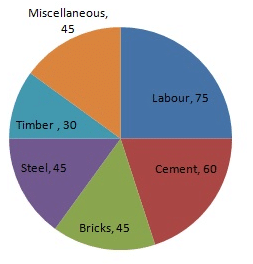
PAGE NO 25.13:
Question 11:
The following table shows how a student spends his pocket money during the course of a month. Represent it by a pie-diagram.
| Items | Food | Entertainment | Other expenditure | Savings |
| Expenditure | 40% | 25% | 20% | 15% |
Ans.
We know:
Central angle of a component = (component value/sum of component values × 360)
Here, total expenditure = 100%
Thus, central angle for each component can be calculated as follows:
| Item | Expenditure (in %) | Sector angles |
| Food | 40 | 40/100 × 360 = 144 |
| Entertainment | 25 | 25/100 × 360 = 90 |
| Other expenditures | 20 | 20/100 × 360 = 72 |
| Savings | 15 | 15/100 × 360 = 54 |
Now, the pie chat representing the given data can be constructed by following the steps below:
Step 1 : Draw circle of an appropriate radius.
Step 2 : Draw a vertical radius of the circle drawn in step 1.
Step 3 : Choose the largest central angle. Here the largest central angle is 144o. Draw a sector with the central angle 144o in such a way that one of its radii coincides with the radius drawn in step 2 and another radius is in its counter clockwise direction.
Step 4 : Construct other sectors representing the other items in the clockwise sense in descending order of magnitudes of their central angles.
Step 5 : Shade the sectors with different colours and label them, as shown as in figure below.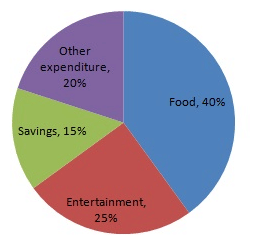
FAQs on Chapter 25 - Data Handling-III (Part - 1), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the importance of data handling in mathematics? |  |
| 2. How can data be represented graphically? |  |
| 3. What is the difference between mean, median, and mode? |  |
| 4. How can outliers affect the measures of central tendency? |  |
| 5. How can we calculate the range of a data set? |  |


















