Chapter 26 - Data Handling-IV (Probability), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 26. 14:
Question 1:
The probability that it will rain tomorrow is 0. 85. What is the probability that it will not rain tomorrow?
Ans.
Let A be the event of raining tomorrow. The probability that it will rain tomorrow, P(A), is 0. 85.
Since the event of raining tomorrow and not raining tomorrow are complementary to each other, the probability of not raining tomorrow is:
P(A) = 1 − P(A) = 1 − 0. 85 = 0. 15
Let A be the event of raining tomorrow. The probability that it will rain tomorrow, PA, is 0. 85.
Since the event of raining tomorrow and not raining tomorrow are complementary to each other, the probability of not raining tomorrow is: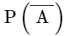 = 1 - PA = 1 - 0. 85 = 0. 15
= 1 - PA = 1 - 0. 85 = 0. 15
Question 2:
A die is thrown. Find the probability of getting:
(i) a prime number
(ii) 2 or 4
(iii) a multiple of 2 or 3
Ans.
When a die is thrown, the possible outcomes are 1, 2, 3, 4, 5 and 6. Thus, the sample space will be as follows: S = {1,2,3,4,5,6}
(i) Let A be the event of getting a prime number. There are 3 prime numbers (2,3 and 5) in the sample space. Thus, the number of favourable outcomes is 3.
Hence, the probability of getting a prime number is as follows:P(A) =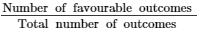 = 3/6 = 1/2
= 3/6 = 1/2
(ii) Let A be the event of getting a two or four. Two or four occurs once in a single roll. Therefore, the total number of favourable outcomes is 2.
Hence, the probability of getting 2 or 4 is as follows:P(A) = 2/6 = 1/3
(iii) Let A be the event of getting multiples of 2 or 3. Here, the multiples of 2 are 2, 4, 6 and the multiples of 3 are 3 and 6. Therefore, the favourable outcomes are 2, 3, 4 and 6.
Hence, the probability of getting a multiple of 2 or 3 is as follows:P(A) = 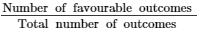 = 4/6 = 2/3
= 4/6 = 2/3
PAGE NO 26. 15:
Question 3:
In a simultaneous throw of a pair of dice, find the probability of getting:
(i) 8 as the sum
(ii) a doublet
(iii) a doublet of prime numbers
(iv) a doublet of odd numbers
(v) a sum greater than 9
(vi) an even number on first
(vii) an even number on one and a multiple of 3 on the other
(viii) neither 9 nor 11 as the sum of the numbers on the faces
(ix) a sum less than 6
(x) a sum less than 7
(xi) a sum more than 7
(xii) at least once
(xiii) a number other than 5 on any dice.
Ans.
When a pair of dice is thrown simultaneously, the sample space will be as follows:S = {(1,1), (1,2), (1,3), (1,4),⋯(6,5), (6,6)} Hence, the total number of outcomes is 36.
(i) Let A be the event of getting pairs whose sum is 8. Now, the pairs whose sum is 8 are (2,6), (3,5), (4,4), (5,3) and (6,2).
Therefore, the total number of favourable outcomes is 5.
∴ P(A) =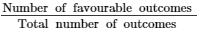 = 5/36 (ii) Let A be the event of getting doublets in the sample space.
= 5/36 (ii) Let A be the event of getting doublets in the sample space.
The doublets in the sample space are (1,1), (2,2), (3,3), (4,4), (5,5) and (6,6). Hence, the number of favourable outcomes is 6.
∴ P(A) = 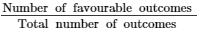 = 6/36 = 1/6 (iii) Let A be the event of getting doublets of prime numbers in the sample space.
= 6/36 = 1/6 (iii) Let A be the event of getting doublets of prime numbers in the sample space.
The doublets of prime numbers in the sample space are (2,2), (3,3) and (5,5). Hence, the number of favourable outcomes is 3.
∴ P(A) = 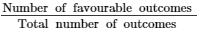 = 3/36 = 1/12
= 3/36 = 1/12
(iv) Let A be the event of getting doublets of odd numbers in the sample space. The doublets of odd numbers in the sample space are (1,1), (3,3) and (5,5).
Hence, the number of favourable outcomes is 3.
∴ P(A) = 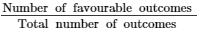 = 3/36 = 1/12
= 3/36 = 1/12
(v)Let A be the event of getting pairs whose sum is greater than 9. The pairs whose sum is greater than 9 are (4,6),(5,5), (5,6),(6,4),(6,5) and (6,6).
Hence, the number of favorable outcomes is 6.
∴ P(A) = 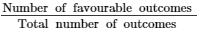 = 6/36 = 1/6
= 6/36 = 1/6
(vi)Let A be the event of getting pairs who has even numbers on first in the sample space. The pairs who has even numbers on first are: (2,1), (2,2),…(2,6), (4,1),⋯,(4,6), (6,1),⋯(6,6).
Hence, the number of favourable outcomes is 18.
∴ P(A) = 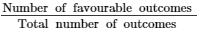 = 18/36 = 1/3
= 18/36 = 1/3
(vii)Let A be the event of getting pairs with an even number on one die and a multiple of 3 on the other.
The pairs with an even number on one die and a multiple of 3 on the other are (2,3), (2,6), (4,3), (4,6), (6,3) and (6,6). Hence, the number of favourable outcomes is 6.
∴ P(A) = 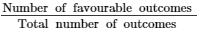 = 6/36 = 1/6
= 6/36 = 1/6
(viii) Let A be the event of getting pairs whose sum is 9 or 11. The pairs whose sum is 9 are (3,6), (4,5), (5,4) and (6,3). And, the pairs whose sum is 11 are (5,6) and (6,5). Hence, the number of favourable outcomes is 6.
∴ P(A) = 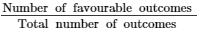 = 6/36 = 1/6
= 6/36 = 1/6
∴ P(sum of the pairs with neither 9 nor 11) = 1 − P(sum of the pairs having 9 or 11) = 1 − 16 = 56
(ix) Let A be the event of getting pairs whose sum is less than 6. The pairs whose sum is less than 6 are (1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (3,1), (3,2) and (4,1). Hence, the number of favourable outcomes is 10.
∴ P(A) = 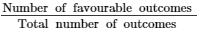 = 10/36 = 5/18
= 10/36 = 5/18
(x) Let A be the event of getting pairs whose sum is less than 7.
The pairs whose sum is less than 7 are (1,1), (1,2), (1,3), (1,4), (1,5), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (4,1), (4,2) and (5,1).
Hence, the number of favourable outcomes is 15.
∴ P(A) =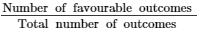 = 15/36 = 5/12
= 15/36 = 5/12
(xi)Let A be the event of getting pairs whose sum is more than 7.
The pairs whose sum is more than 7 are (2,6), (3,5), (3,6), (4,4), (4,5), (4,6), (5,3), (5,4), (5,5), (5,6), (6,2), (6,3), (6,4), (6,5) and (6,6).
Hence, the number of favourable outcomes is 15.
∴ P(A) = 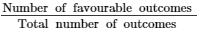 = 15/36 = 5/12
= 15/36 = 5/12
(xii) Incomplete question
(xiii)Let A be the event of getting pairs that has the number 5.
The pairs that has the number 5 are (1,5), (2,5), (3,5), (4,5), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4) and (6,6).
Hence, the number of favourable outcomes is 11.
∴ P(A) = 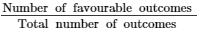 = 11/36
= 11/36
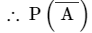 = 1−P(A) = 1−1136 = 25/36
= 1−P(A) = 1−1136 = 25/36
Question 4:
Three coins are tossed together. Find the probability of getting:
(i) exactly two heads
(ii) at least two heads
(iii) at least one head and one tail
(iv) no tails
Ans.
When 3 coins are tossed together, the outcomes are as follows:S = {(h,h,h), (h,h,t), (h,t,h), (h,t,t), (t,h,h), (t,h,t), (t,t,h), (t,t,t)}Therefore, the total number of outcomes is 8.
(i) Let A be the event of getting triplets having exactly 2 heads. Triplets having exactly 2 heads: (h,h,t), (h,t,h), (t,h,h)Therefore, the total number of favourable outcomes is 3. P(A) = 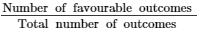 = 3/8
= 3/8
(ii) Let A be the event of getting triplets having at least 2 heads.
Triplets having at least 2 heads: (h,h,t), (h,t,h), (t,h,h), (h,h,h)
Therefore, the total number of favourable outcomes is 4.
P(A) = 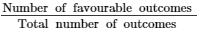 = 4/8 = 1/2
= 4/8 = 1/2
(iii) Let A be the event of getting triplets having at least one head and one tail.
Triplets having at least one head and one tail: (h,h,t), (h,t,h), (t,h,h), (h,h,t), (t,t,h), (t,h,t)
Therefore, the total number of favourable outcomes is 6.
P(A) = 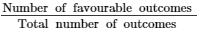 = 6/8 = 3/4
= 6/8 = 3/4
(iv) Let A be the event of getting triplets having no tail. Triplets having no tail: (h,h,h)
Therefore, the total number of favourable outcomes is 1.
P(A) = 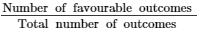 = 1/8
= 1/8
Question 5:
A card is drawn at random from a pack of 52 cards. Find the probability that the card drawn is:
(i) a black king
(ii) either a black card or a king
(iii) black and a king
(iv) a jack, queen or a king
(v) neither a heart nor a king
(vi) spade or an ace
(vii) neither an ace nor a king
(viii) neither a red card nor a queen.
(ix) other than an ace
(x) a ten
(xi) a spade
(xii) a black card
(xiii) the seven of clubs
(xiv) jack
(xv) the ace of spades
(xvi) a queen
(xvii) a heart
(xviii) a red card
Ans.
(i) There are two black kings, spade and clover. Hence, the probability that the drawn card is a black king is: 2/52 = 1/26
(ii) There are 26 black cards and 4 kings, but two kings are already black. Hence, we only need to count the red kings. Thus, the probability is: (26+2)/52 = 7/13
(iii) This question is exactly the same as part (i) . Hence, the probability is: 2/52 = 1/26
(iv) There are 4 jacks, 4 queens and 4 kings in a deck. Hence, the probability of drawing either of them is: (4+4+4)/52 = 3/13
(v) This means that we have to leave the hearts and the kings out. There are 13 hearts and 3 kings (other than that of hearts). Hence, the probability of drawing neither a heart nor a king is: (52-13-3)/52 = 9/13
(vi) There are 13 spades and 3 aces (other than that of spades). Hence the probability is: (13+3)/52 = 4/13
(vii) This means that we have to leave the aces and the kings out. There are 4 aces and 4 kings. Hence, the probability of drawing neither an ace nor a king is: (52−-4−-4)/52 = 11/13.
(viii) This means that we have to leave the red cards and the queens out. There are 26 red cards and 2 queens (only black queens are counted since the reds are already counted among the red cards). Hence, the probability of drawing neither a red card nor a queen is: (52-26-2)/52 = 6/13
(ix) It means that we have to leave out the aces. Since there are 4 aces, then the probability is (52−4)/52 = 12/13
(x) Since there are four 10s, the probability is: 4/52 = 1/13
(xi) Since there are 13 spades, the probability is: 13/52 = 1/4
(xii) Since there are 26 black cards, the probability is: 26/52 = 1/2
(xiii) There is only one card named seven of clubs. Hence, the probability is 1/52.
(xiv) Since there are 4 jacks, the probability is: 4/52 = 1/13
(xv) There is only 1 card named ace of spade. Hence, the probability is 1/52.
(xvi) Since there are 4 queens, the probability is: 4/52 = 1/13
(xvii) Since there are 13 hearts, the probability is: 13/52 = 1/4
(xviii) Since there are 26 red cards, the probability is 26/52 = 1/2
Question 6:
An urn contains 10 red and 8 white balls. One ball is drawn at random. Find the probability that the ball drawn is white.
Ans.
Number of red balls = 10
Number of white balls = 8
Total number of balls in the urn = 10 + 8 = 18
Therefore, the total number of cases is 18 and the number of favourable cases is 8.
∴ P(The ball drawn is white) = 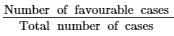 = 8/18 = 4/9
= 8/18 = 4/9
Question 7:
A bag contains 3 red balls, 5 black balls and 4 white balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is:
(i) white?
(ii) red?
(iii) black?
(iv) not red?
Ans.
Number of red balls = 3
Number of black balls = 5
Number of white balls = 4
Total number of balls = 3 + 5 + 4 = 12
Therefore, the total number of cases is 12.
(i) Since there are 4 white balls, the number of favourable outcomes is 4.
P(a white ball) = 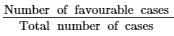 = 4/12 = 1/3
= 4/12 = 1/3
(ii) Since there are 3 red balls, the number of favourable outcomes is 3.
P(a red ball) = 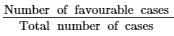 = 3/12 = 1/4
= 3/12 = 1/4
(iii) Since there are 5 black balls, the number of favourable outcomes is 5.
P(a black ball) = 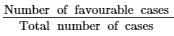 = 5/12
= 5/12
(iv) P(not a red ball) = 1−P(a red ball) = 1−1/4 = 3/4
Question 8:
What is the probability that a number selected from the numbers 1, 2, 3, . . . , 15 is a multiple of 4?
Ans.
There are 15 numbers from 1, 2,⋯,15. Hence, the total number of cases is 15. Again, the multiples of 4 are 4, 8 and 12. Therefore, the total number of favourable cases is 3.
∴ P(the number is a multiple of 4) = 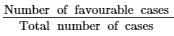 = 3/15 = 1/5
= 3/15 = 1/5
Question 9:
A bag contains 6 red, 8 black and 4 white balls. A ball is drawn at random. What is the probability that ball drawn is not black?
Ans.
Number of red balls = 6
Number of black balls = 8
Number of white balls = 4
Total number of balls = 6 + 8 + 4 = 18
∴ Total number of cases = 18
Again, number of balls that are not black = 18 − 8 = 10
Thus, the number of favourable cases is 10.
∴ P(the drawn ball is not black) = 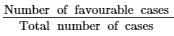 = 10/18 = 5/9
= 10/18 = 5/9
Question 10:
A bag contains 5 white and 7 red balls. One ball is drawn at random. What is the probability that ball drawn is white?
Ans.
Number of white balls = 5
Number of red balls = 7
Total number of balls = 5 + 7 = 12
∴ The total number of cases = 12
Again, there are 5 white balls. Therefore, the number of favourable outcomes is 5.
∴ P(the drawn ball is white) = 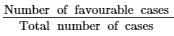 = 5/12
= 5/12
Question 11:
A bag contains 4 red, 5 black and 6 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is:
(i) white
(ii) red
(iii) not black
(iv) red or white
Ans.
Number of red balls = 4
Number of black balls = 5
Number of white balls = 6
Total number of balls in the bag = 4 + 5 + 6 = 15
Therefore, the total number of cases is 15.
(i) Let A denote the event of getting a white ball. Number of favourable outcomes, i. e. number of white balls =
P(A) = 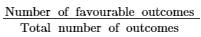 = 6/15 = 2/5
= 6/15 = 2/5
(ii) Let B denote the event of getting a red ball. Number of favourable outcomes, i. e. number of red balls = 4
P(B) = 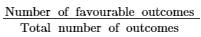 = 4/15
= 4/15
(iii) Let C denote the event of getting a black ball. Number of favourable outcomes, i. e. number of black balls = 5
P(C) = 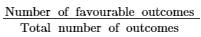 = 5/15 = 1/3
= 5/15 = 1/3
Therefore, the probabilty of not getting a black ball is as follows:
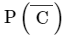 = 1 − P(C) = 1 − 1/3 = 2/3
= 1 − P(C) = 1 − 1/3 = 2/3
(iv) Let D denote the event of getting a red or a white ball. P(D) = 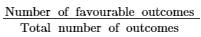 =
= 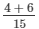 = 10/15 = 2/5
= 10/15 = 2/5
Question 12:
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is:
(i) red
(ii) black
Ans.
Number of red balls = 3
Number of black balls = 5
Total number of balls = 3 + 5 = 8
(i) Let A be the event of drawing a red ball.
∴ P(A) = 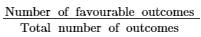 = 3/8
= 3/8
(ii) Let B be the event of drawing a black ball.
∴ P(B) = 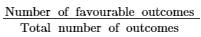 = 5/8
= 5/8
Question 13:
A bag contains 5 red marbles, 8 white marbles, 4 green marbles. What is the probability that if one marble is taken out of the bag at random, it will be
(i) red
(ii) white
(iii) not green
Ans.
Number of red marbles = 5
Number of white marbles = 8
Number of green marbles = 4
Total number of marbles in the bag = 5 + 8 + 4 = 17
∴ Total number outcomes = 17
(i) Let A be the event of drawing a red ball.
∴ P(A) = 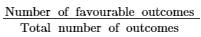 = 5/17
= 5/17
(ii) Let B be the event of drawing a white ball.
∴ P(B) = 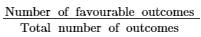 = 8/17
= 8/17
(iii) Let C be the event of drawing a green ball.
∴ P(C) = 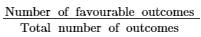 = 4/17
= 4/17
Now, the event of not drawing a green ball is:
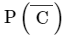 = 1 − P(C) = 1 − 4/17 = 13/17
= 1 − P(C) = 1 − 4/17 = 13/17
PAGE NO 26. 16:
Question 14:
If you put 21 consonants and 5 vowels in a bag. What would carry greater probability? Getting a consonant or a vowel? Find each probability.
Ans.
Number of consonants = 21
Number of vowels = 5
Total number of possible outcomes = 21 + 5 = 26
Let C be the event of getting a consonant and V be the event of getting a vowel.
∴ P(C) = 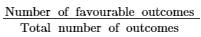 = 21/26 And,
= 21/26 And,
P(V) = 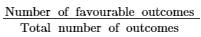 = 5/26
= 5/26
Thus, the consonants have a greater probability.
Question 15:
If we have 15 boys and 5 girls in a class which carries a higher probability? Getting a copy belonging to a boy or a girl. Can you give it a value?
Ans.
Number of boys in the class = 15
Number of girls in the class = 5
Total number of students in the class = 15 + 5 = 20
∴ Number of possible outcomes = 20
Since the number of boys is more than the number of girls, boys will have a higher probability. Hence, there is the higher probability of getting a copy belonging to a boy. Let A be the event of getting a boy's copy and B be the event of getting a girl's copy.
∴ P(A) = 15/20 = 3/4
And, P(B) = 5/20 = 1/4
Question 16:
If you have a collection of 6 pairs of white socks and 3 pairs of black socks. What is the probability that a pair you pick without looking is
(i) white?
(ii) black?
Ans.
Number of pairs of white socks = 6
Number of pairs of black socks = 3
Total number of pairs of socks = 6 + 3 = 9
∴ Number of possible outcomes = 9
(i) Let A be the event of getting a pair of white socks.
∴ P(A) = 6/9 = 2/3
(ii) Let B be the event of getting a pair of black socks.
∴ P(B) = 3/9 = 1/3
Question 17:
If you have a spinning wheel with 3-green sectors, 1-blue sector and 1-red sector. What is the probability of getting a green sector? Is it the maximum?
Ans.
Number of green sectors in the wheel = 3
Number of blue sectors in the wheel = 1
Number of red sectors in the wheel = 1
Total number of sectors in the wheel = 3 + 1 + 1 = 5
∴ Number of possible outcomes = 5
Let A, B and C be the events of getting a green, blue and red sector, respectively.
∴ P(A) = 3/5, P(B) = 1/5 and P(C) = 1/5
Hence, the probability of getting a green sector is the maximum.
Question 18:
When two dice are rolled:
(i) List the outcomes for the event that the total is odd.
(ii) Find probability of getting an odd total.
(iii) List the outcomes for the event that total is less than 5.
(iv) Find the probability of getting a total less than 5?
Ans.
Possible outcomes when two dice are rolled:S = {(1,1), (1,2), (1,3), (1,4),⋯,(6,5), (6,6)}Therefore, the number of possible outcomes in the sample space is 36.
(i) The outcomes for the event that the total is odd:E = {(1,2), (1,4), (1,6), (2,1), (2,3), (2,5), (3,2), (3,4), (3,6), (4,1), (4,3), (4,5), (5,2), (5,4), (5,6), (6,1), (6,3), (6,5)}
(ii) The number of favourable outcomes is 18.
∴ P(E) = 18/36 = 1/2
(iii) The outcomes for the event that total is less than 5:B = {(1,1),(1,2),(1,3),(2,1),(2,2),(3,1)}
(iv) The number of favourable outcomes is 6.
∴ P(B) = 6/36 = 1/6
FAQs on Chapter 26 - Data Handling-IV (Probability), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is probability in data handling? |  |
| 2. How is probability calculated in data handling? |  |
| 3. What are the different types of probability in data handling? |  |
| 4. How can probability be used in data handling? |  |
| 5. Can probability be greater than 1? |  |


















