Class 8 Exam > Class 8 Notes > RD Sharma Solutions for Class 8 Mathematics > RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.2) Part - 2, Class 8 Math
Chapter 3 - Squares and Square Roots (Ex-3.2) Part - 2, Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 8: Observe the following pattern
(1×2)+(2×3)=
(1×2)+(2×3)+(3×4)=
(1×2)+(2×3)+(3×4)+(4×5)=
and find the value of
(1 × 2) + (2 × 3) + (3 × 4) + (4 × 5) + (5 × 6)
Answer 8: The RHS of the three equalities is a fraction whose numerator is the multiplication of three consecutive numbers and whose denominator is 3.
If the biggest number (factor) on the LHS is 3, the multiplication of the three numbers on the RHS begins with 2.
If the biggest number (factor) on the LHS is 4, the multiplication of the three numbers on the RHS begins with 3.
If the biggest number (factor) on the LHS is 5, the multiplication of the three numbers on the RHS begins with 4.
Using this pattern, (1 x 2) + (2 x 3) + (3 x 4) + (4 x 5) + (5 x 6) has 6 as the biggest number. Hence, the multiplication of the three numbers on the RHS will begin with 5. Finally, we have:
1 × 2 + 2 ×3 + 3 × 4 + 4 × 5 + 5 × 6 = = 70
= 70
(1×2)+(2×3)=
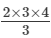
(1×2)+(2×3)+(3×4)=
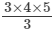
(1×2)+(2×3)+(3×4)+(4×5)=
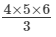
and find the value of
(1 × 2) + (2 × 3) + (3 × 4) + (4 × 5) + (5 × 6)
Answer 8: The RHS of the three equalities is a fraction whose numerator is the multiplication of three consecutive numbers and whose denominator is 3.
If the biggest number (factor) on the LHS is 3, the multiplication of the three numbers on the RHS begins with 2.
If the biggest number (factor) on the LHS is 4, the multiplication of the three numbers on the RHS begins with 3.
If the biggest number (factor) on the LHS is 5, the multiplication of the three numbers on the RHS begins with 4.
Using this pattern, (1 x 2) + (2 x 3) + (3 x 4) + (4 x 5) + (5 x 6) has 6 as the biggest number. Hence, the multiplication of the three numbers on the RHS will begin with 5. Finally, we have:
1 × 2 + 2 ×3 + 3 × 4 + 4 × 5 + 5 × 6 =
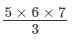 = 70
= 70Question 9: Observe the following pattern
1=1/2 {1×(1+1)} 1+2=1/2 {2×(2+1)}
1+2+3=1/2 {3×(3+1)}
1+2+3+4=1/2{ 4×(4+1)} and find the values of each of the following:
(i) 1 + 2 + 3 + 4 + 5 + ... + 50
(ii) 31 + 32 + ... + 50
Answer 9: Observing the three numbers for right hand side of the equalities:
The first equality, whose biggest number on the LHS is 1, has 1, 1 and 1 as the three numbers.
The second equality, whose biggest number on the LHS is 2, has 2, 2 and 1 as the three numbers.
The third equality, whose biggest number on the LHS is 3, has 3, 3 and 1 as the three numbers.
The fourth equality, whose biggest number on the LHS is 4, has 4, 4 and 1 as the three numbers.
Hence, if the biggest number on the LHS is n, the three numbers on the RHS will be n, n and 1.
Using this property, we can calculate the sums for (i) and (ii) as follows:
(i) 1 + 2 + 3 +........ + 50 = 12 × 50 × (50 + 1) = 1275
(ii) The sum can be expressed as the difference of the two sums as follows:
31 + 32 + .....+ 50 = (1 + 2 + 3 + ......+ 50) − ( 1 + 2 + 3 + ......+30)
The result of the first bracket is exactly the same as in part (i).
1 + 2 + ....+ 50 = 1275
Then, the second bracket:
1+2+......+30 = 1/2 (30×(30+1))
Finally, we have:
31 + 32 + .... + 50 = 1275 − 465 = 810
1=1/2 {1×(1+1)} 1+2=1/2 {2×(2+1)}
1+2+3=1/2 {3×(3+1)}
1+2+3+4=1/2{ 4×(4+1)} and find the values of each of the following:
(i) 1 + 2 + 3 + 4 + 5 + ... + 50
(ii) 31 + 32 + ... + 50
Answer 9: Observing the three numbers for right hand side of the equalities:
The first equality, whose biggest number on the LHS is 1, has 1, 1 and 1 as the three numbers.
The second equality, whose biggest number on the LHS is 2, has 2, 2 and 1 as the three numbers.
The third equality, whose biggest number on the LHS is 3, has 3, 3 and 1 as the three numbers.
The fourth equality, whose biggest number on the LHS is 4, has 4, 4 and 1 as the three numbers.
Hence, if the biggest number on the LHS is n, the three numbers on the RHS will be n, n and 1.
Using this property, we can calculate the sums for (i) and (ii) as follows:
(i) 1 + 2 + 3 +........ + 50 = 12 × 50 × (50 + 1) = 1275
(ii) The sum can be expressed as the difference of the two sums as follows:
31 + 32 + .....+ 50 = (1 + 2 + 3 + ......+ 50) − ( 1 + 2 + 3 + ......+30)
The result of the first bracket is exactly the same as in part (i).
1 + 2 + ....+ 50 = 1275
Then, the second bracket:
1+2+......+30 = 1/2 (30×(30+1))
Finally, we have:
31 + 32 + .... + 50 = 1275 − 465 = 810
Question 10: Observe the following pattern12=1/6 [1×(1+1)×(2×1+1)]12+22=1/6 [2×(2+1)×(2×2+1)]12+22+32=1/6 [3×(3+1)×(2×3+1)12+22+32+42=1/6 [4×(4+1)×(2×4+1)]and find the values of each of the following:
(i) 12 + 22 + 32 + 42 + ... + 102
(ii) 52 + 62 + 72 + 82 + 92 + 102 + 112 + 122 Answer 10: Observing the six numbers on the RHS of the equalities:
The first equality, whose biggest number on the LHS is 1, has 1, 1, 1, 2, 1 and 1 as the six numbers.
The second equality, whose biggest number on the LHS is 2, has 2, 2, 1, 2, 2 and 1 as the six numbers.
The third equality, whose biggest number on the LHS is 3, has 3, 3, 1, 2, 3 and 1 as the six numbers.
The fourth equality, whose biggest number on the LHS is 4, has numbers 4, 4, 1, 2, 4 and 1 as the six numbers.
Note that the fourth number on the RHS is always 2 and the sixth number is always 1. The remaining numbers are equal to the biggest number on the LHS.
Hence, if the biggest number on the LHS is n, the six numbers on the RHS would be n, n, 1, 2, n and 1.
Using this property, we can calculate the sums for (i) and (ii) as follows:
(i) 12 + 22 + .......+ 102 = 1/6 ×[10×(10+1)×(2×10+1)]=1/+6× [10 × 11 × 12= 385(ii) The sum can be expressed as the difference of the two sums as follows:52 + 62 +.......+ 122 = ( 12 + 22 +......+122) − ( 12 + 22 +......+42)The sum of the first bracket on the RHS: 12 + 22 +.....+122 =1/6 [12×(12+1)×(2×12+1)] = 650The second bracket is:
12 + 22 + ......+ 42
= 1/6 ×[4×(4+1)×(2×4+1)]
=1/6 × 4 × 5 × 9 = 30
Finally, the wanted sum is: 52 + 62 + ...... + 122= (12 + 22 +..... + 122) − ( 12 + 22 +..... + 122)=650 − 30 = 62Question 11: Which of the following numbers are squares of even numbers?
121, 225, 256, 324, 1296, 6561, 5476, 4489, 373758
Answer 11: The numbers whose last digit is odd can never be the square of even numbers. So, we have to leave out 121, 225, 6561 and 4489, leaving only 256, 324, 1296, 5476 and 373758. For each number, use prime factorisation method and make pairs of equal factors.
(i) 256 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
= (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2)
There are no factors that are not paired. Hence, 256 is a perfect square. The square of an even number is always even. Hence, 256 is the square of an even number.
(ii) 324 = 2 x 2 x 3 x 3 x 3 x 3
= (2 x 2) x (3 x 3) x (3 x 3)
There are no factors that are not paired. Hence, 324 is a perfect square. The square of an even number is always even. Hence, 324 is the square of an even number.
(iii)1296 = 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3
= (2 x 2) x (2 x 2) x (3 x 3) x (3 x 3)
There are no factors that are not paired. Hence, 1296 is a perfect square. The square of an even number is always even. Hence, 1296 is the square of an even number.
(iv) 5476 = 2 x 2 x 37 x 37
= (2 x 2) x (37 x 37)
There are no factors that are not paired. Hence, 5476 is a perfect square. The square of an even number is always even. Hence, 5476 is the square of an even number.
(v) 373758 = 2 x 3 x 7 x 11 x 809
Here, each factor appears only once, so grouping them into pairs of equal factors is not possible. It means that 373758 is not the square of an even number.
Hence, the numbers that are the squares of even numbers are 256, 324, 1296 and 5476.
Question 12: By just examining the units digits, can you tell which of the following cannot be whole squares?
(i) 1026
(ii) 1028
(iii) 1024
(iv) 1022
(v) 1023
(vi) 1027
Answer 12: If the units digit of a number is 2, 3, 7 or 8, the number cannot be a whole square.
(i) 1026 has 6 as the units digit, so it is possibly a perfect square.
(ii) 1028 has 8 as the units digit, so it cannot be a perfect square.
(iii) 1024 has 4 as the units digit, so it is possibly a perfect square.
(iv) 1022 has 2 as the units digit, so it cannot be a perfect square.
(v) 1023 has 3 as the units digit, so it cannot be a perfect square.
(vi) 1027 has 7 as the unit digit, so it cannot be a perfect square.
Hence, by examining the units digits, we can be certain that 1028, 1022, 1023 and 1027 cannot be whole squares.
QUESTION 13: WRITE FIVE NUMBERS FOR WHICH YOU CANNOT DECIDE WHETHER THEY ARE SQUARES.
ANSWER 13: A number whose unit digit is 2, 3, 7 or 8 cannot be a perfect square.
On the other hand, a number whose unit digit is 1, 4, 5, 6, 9 or 0 might be a perfect square (although we will have to verify whether it is a perfect square or not).
Applying the above two conditions, we cannot quickly decide whether the following numbers are squares of any numbers:
1111, 1444, 1555, 1666, 1999
QUESTION 14: WRITE FIVE NUMBERS WHICH YOU CANNOT DECIDE WHETHER THEY ARE SQUARE JUST BY LOOKING AT THE UNIT'S DIGIT.
ANSWER 14: A number whose unit digit is 2, 3, 7 or 8 cannot be a perfect square.
On the other hand, a number whose unit digit is 1, 4, 5, 6, 9 or 0 might be a perfect square although we have to verify that.
Applying these two conditions, we cannot determine whether the following numbers are squares just by looking at their unit digits:
1111, 1001, 1555, 1666 and 1999
Question 15: Write true (T) or false (F) for the following statements.
(i) The number of digits in a square number is even.
(ii) The square of a prime number is prime.
(iii) The sum of two square numbers is a square number.
(iv) The difference of two square numbers is a square number.
(v) The product of two square numbers is a square number.
(vi) No square number is negative.
(vii) There is no square number between 50 and 60.
(viii) There are fourteen square number upto 200.
Answer 15: (i) False
Example: 100 is the square of a number but its number of digits is three, which is not an even number.
(ii) False
If p is a prime number, its square is p2, which has at least three factors: 1, p and p2. Since it has more than two factors, it is not a prime number.
(iii) False
1 is the square of a number (1 = 12). But 1 + 1 = 2, which is not the square of any number.
(iv) False
4 and 1 are squares (4 = 22, 1 = 12). But 4 − 1 = 3, which is not the square of any number.
(v) True
If a2 and b2 are two squares, their product is a2 x b2 = (a x b)2, which is a square.
(vi) True
The square of a negative number will be positive because negative times negative is positive.
(vii) True
72 = 49 and 82 = 64. 7 and 8 are consecutive numbers and hence there are no square numbers between 50 and 60.
(viii) True
142 is equal to 196, which is below 200. There are 14 square numbers below 200.
(i) 12 + 22 + 32 + 42 + ... + 102
(ii) 52 + 62 + 72 + 82 + 92 + 102 + 112 + 122 Answer 10: Observing the six numbers on the RHS of the equalities:
The first equality, whose biggest number on the LHS is 1, has 1, 1, 1, 2, 1 and 1 as the six numbers.
The second equality, whose biggest number on the LHS is 2, has 2, 2, 1, 2, 2 and 1 as the six numbers.
The third equality, whose biggest number on the LHS is 3, has 3, 3, 1, 2, 3 and 1 as the six numbers.
The fourth equality, whose biggest number on the LHS is 4, has numbers 4, 4, 1, 2, 4 and 1 as the six numbers.
Note that the fourth number on the RHS is always 2 and the sixth number is always 1. The remaining numbers are equal to the biggest number on the LHS.
Hence, if the biggest number on the LHS is n, the six numbers on the RHS would be n, n, 1, 2, n and 1.
Using this property, we can calculate the sums for (i) and (ii) as follows:
(i) 12 + 22 + .......+ 102 = 1/6 ×[10×(10+1)×(2×10+1)]=1/+6× [10 × 11 × 12= 385(ii) The sum can be expressed as the difference of the two sums as follows:52 + 62 +.......+ 122 = ( 12 + 22 +......+122) − ( 12 + 22 +......+42)The sum of the first bracket on the RHS: 12 + 22 +.....+122 =1/6 [12×(12+1)×(2×12+1)] = 650The second bracket is:
12 + 22 + ......+ 42
= 1/6 ×[4×(4+1)×(2×4+1)]
=1/6 × 4 × 5 × 9 = 30
Finally, the wanted sum is: 52 + 62 + ...... + 122= (12 + 22 +..... + 122) − ( 12 + 22 +..... + 122)=650 − 30 = 62Question 11: Which of the following numbers are squares of even numbers?
121, 225, 256, 324, 1296, 6561, 5476, 4489, 373758
Answer 11: The numbers whose last digit is odd can never be the square of even numbers. So, we have to leave out 121, 225, 6561 and 4489, leaving only 256, 324, 1296, 5476 and 373758. For each number, use prime factorisation method and make pairs of equal factors.
(i) 256 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
= (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2)
There are no factors that are not paired. Hence, 256 is a perfect square. The square of an even number is always even. Hence, 256 is the square of an even number.
(ii) 324 = 2 x 2 x 3 x 3 x 3 x 3
= (2 x 2) x (3 x 3) x (3 x 3)
There are no factors that are not paired. Hence, 324 is a perfect square. The square of an even number is always even. Hence, 324 is the square of an even number.
(iii)1296 = 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3
= (2 x 2) x (2 x 2) x (3 x 3) x (3 x 3)
There are no factors that are not paired. Hence, 1296 is a perfect square. The square of an even number is always even. Hence, 1296 is the square of an even number.
(iv) 5476 = 2 x 2 x 37 x 37
= (2 x 2) x (37 x 37)
There are no factors that are not paired. Hence, 5476 is a perfect square. The square of an even number is always even. Hence, 5476 is the square of an even number.
(v) 373758 = 2 x 3 x 7 x 11 x 809
Here, each factor appears only once, so grouping them into pairs of equal factors is not possible. It means that 373758 is not the square of an even number.
Hence, the numbers that are the squares of even numbers are 256, 324, 1296 and 5476.
Question 12: By just examining the units digits, can you tell which of the following cannot be whole squares?
(i) 1026
(ii) 1028
(iii) 1024
(iv) 1022
(v) 1023
(vi) 1027
Answer 12: If the units digit of a number is 2, 3, 7 or 8, the number cannot be a whole square.
(i) 1026 has 6 as the units digit, so it is possibly a perfect square.
(ii) 1028 has 8 as the units digit, so it cannot be a perfect square.
(iii) 1024 has 4 as the units digit, so it is possibly a perfect square.
(iv) 1022 has 2 as the units digit, so it cannot be a perfect square.
(v) 1023 has 3 as the units digit, so it cannot be a perfect square.
(vi) 1027 has 7 as the unit digit, so it cannot be a perfect square.
Hence, by examining the units digits, we can be certain that 1028, 1022, 1023 and 1027 cannot be whole squares.
QUESTION 13: WRITE FIVE NUMBERS FOR WHICH YOU CANNOT DECIDE WHETHER THEY ARE SQUARES.
ANSWER 13: A number whose unit digit is 2, 3, 7 or 8 cannot be a perfect square.
On the other hand, a number whose unit digit is 1, 4, 5, 6, 9 or 0 might be a perfect square (although we will have to verify whether it is a perfect square or not).
Applying the above two conditions, we cannot quickly decide whether the following numbers are squares of any numbers:
1111, 1444, 1555, 1666, 1999
QUESTION 14: WRITE FIVE NUMBERS WHICH YOU CANNOT DECIDE WHETHER THEY ARE SQUARE JUST BY LOOKING AT THE UNIT'S DIGIT.
ANSWER 14: A number whose unit digit is 2, 3, 7 or 8 cannot be a perfect square.
On the other hand, a number whose unit digit is 1, 4, 5, 6, 9 or 0 might be a perfect square although we have to verify that.
Applying these two conditions, we cannot determine whether the following numbers are squares just by looking at their unit digits:
1111, 1001, 1555, 1666 and 1999
Question 15: Write true (T) or false (F) for the following statements.
(i) The number of digits in a square number is even.
(ii) The square of a prime number is prime.
(iii) The sum of two square numbers is a square number.
(iv) The difference of two square numbers is a square number.
(v) The product of two square numbers is a square number.
(vi) No square number is negative.
(vii) There is no square number between 50 and 60.
(viii) There are fourteen square number upto 200.
Answer 15: (i) False
Example: 100 is the square of a number but its number of digits is three, which is not an even number.
(ii) False
If p is a prime number, its square is p2, which has at least three factors: 1, p and p2. Since it has more than two factors, it is not a prime number.
(iii) False
1 is the square of a number (1 = 12). But 1 + 1 = 2, which is not the square of any number.
(iv) False
4 and 1 are squares (4 = 22, 1 = 12). But 4 − 1 = 3, which is not the square of any number.
(v) True
If a2 and b2 are two squares, their product is a2 x b2 = (a x b)2, which is a square.
(vi) True
The square of a negative number will be positive because negative times negative is positive.
(vii) True
72 = 49 and 82 = 64. 7 and 8 are consecutive numbers and hence there are no square numbers between 50 and 60.
(viii) True
142 is equal to 196, which is below 200. There are 14 square numbers below 200.
The document Chapter 3 - Squares and Square Roots (Ex-3.2) Part - 2, Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics is a part of the Class 8 Course RD Sharma Solutions for Class 8 Mathematics.
All you need of Class 8 at this link: Class 8
FAQs on Chapter 3 - Squares and Square Roots (Ex-3.2) Part - 2, Class 8 Math RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What are squares and square roots? |  |
Ans. Squares are the product of a number multiplied by itself, while square roots are the inverse operation of finding the number which, when multiplied by itself, gives the given number.
| 2. How do we find the square root of a number? |  |
Ans. To find the square root of a number, we can use the prime factorization method or the long division method. By repeatedly dividing the given number by its factors, we can find the square root.
| 3. Are all numbers perfect squares? |  |
Ans. No, not all numbers are perfect squares. Only numbers that can be expressed as the product of an integer multiplied by itself are perfect squares. For example, 4, 9, 16, etc., are perfect squares.
| 4. Can we find the square root of a negative number? |  |
Ans. No, the square root of a negative number is not a real number. It is called an imaginary number. The square root of a negative number is denoted by "i" (imaginary unit) in mathematics.
| 5. How can square roots be useful in real-life applications? |  |
Ans. Square roots are used in various real-life applications such as calculating distances, determining areas and volumes, designing structures, financial calculations, and in computer graphics. They are also essential in solving quadratic equations.
Related Searches


















