Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 1, Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1:Which of the following numbers are perfect squares?
(i) 484
(ii) 625
(iii) 576
(iv) 941
(v) 961
(vi) 2500
(i) 484 = 222
(ii) 625 = 252
(iii) 576 = 242
(iv) Perfect squares closest to 941 are 900 (302) and 961 (312). Since 30 and 31 are consecutive numbers, there are no perfect squares between 900 and 961. Hence, 941 is not a perfect square.
(v) 961 = 312
(vi) 2500 = 502
Hence, all numbers except that in (iv), i.e. 941, are perfect squares.
Question 2:Show that each of the following numbers is a perfect square. Also, find the number whose square is the given number in each case:
(i) 1156
(ii) 2025
(iii) 14641
(iv) 4761
(i) 1156 = 2 x 2 x 17 x 17
Grouping the factors into pairs of equal factors, we obtain:
1156 = (2 x 2) x (17 x 17)
No factors are left over. Hence, 1156 is a perfect square. Moreover, by grouping 1156 into equal factors:
1156 = (2 x 17) x (2 x 17)
= (2 x 17)2
Hence, 1156 is the square of 34, which is equal to 2 x 17.
(ii) 2025 = 3 x 3 x 3 x 3 x 5 x 5
Grouping the factors into pairs of equal factors, we obtain:
2025 = (3 x 3) x (3 x 3) x (5 x 5)
No factors are left over. Hence, 2025 is a perfect square. Moreover, by grouping 2025 into equal factors:
2025 = (3 x 3 x 5) x (3 x 3 x 5)
= (3 x 3 x 5)2
Hence, 2025 is the square of 45, which is equal to 3 x 3 x 5.
(iii) 14641 = 11 x 11 x 11 x 11
Grouping the factors into pairs of equal factors, we obtain:
14641 = (11 x 11) x (11 x 11)
No factors are left over. Hence, 14641 is a perfect square. The above expression is already grouped into equal factors:
14641 = (11 x 11) x (11 x 11)
= (11 x 11)2
Hence, 14641 is the square of 121, which is equal to 11 x 11.
(iv) 4761 = 3 x 3 x 23 x 23
Grouping the factors into pairs of equal factors, we obtain:
4761 = (3 x 3) x (23 x 23)
No factors are left over. Hence, 4761 is a perfect square. The above expression is already grouped into equal factors:
4761 = (3 x 23) x (3 x 23)
= (3 x 23)2
Hence, 4761 is the square of 69, which is equal to 3 x 23.
Question 3:Find the smallest number by which the given number must bew multiplied so that the product is a perfect square:
(i) 23805
(ii) 12150
(iii) 7688
Factorise each number into its prime factors.
(i) 23805 = 3 x 3 x 5 x 23 x 23
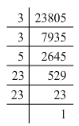
Grouping 23805 into pairs of equal factors:
23805 = (3 x 3) x (23 x 23) x 5
Here, the factor 5 does not occur in pairs. To be a perfect square, every prime factor has to be in pairs. Hence, the smallest number by which 23805 must be multiplied is 5.
(ii) 12150 = 2 x 3 x 3 x 3 x 3 x 3 x 5 x 5
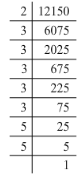
Grouping 12150 into pairs of equal factors:
12150 = (3 x 3 x 3 x 3) x (5 x 5) x 2 x 3
Here, 2 and 3 do not occur in pairs. To be a perfect square, every prime factor has to be in pairs. Hence. the smallest number by which 12150 must be multiplied is 2 x 3, i.e. by 6.
(iii) 7688 = 2 x 2 x 2 x 31 x 31

7688 = (2 x 2) x (31 x 31) x 2
Here, 2 does not occur in pairs. To be a perfect square, every prime factor has to be in pairs. Hence, the smallest number by which 7688 must be multiplied is 2.
(i) 14283
(ii) 1800
(iii) 2904
Answer 4:
For each question, factorise the number into its prime factors.
(i) 14283 = 3 x 3 x 3 x 23 x 23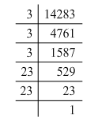
Grouping the factors into pairs:
14283 = (3 x 3) x (23 x 23) x 3
Here, the factor 3 does not occur in pairs. To be a perfect square, all the factors have to be in pairs. Hence, the smallest number by which 14283 must be divided for it to be a perfect square is 3.
(ii) 1800= 2 x 2 x 2 x 3 x 3 x 5 x 5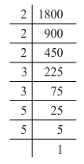
Grouping the factors into pairs:
1800 = (2 x 2) x (3 x 3) x (5 x 5) x 2
Here, the factor 2 does not occur in pairs. To be a perfect square, all the factors have to be in pairs. Hence, the smallest number by which 1800 must be divided for it to be a perfect square is 2.
(iii) 2904 = 2 x 2 x 2 x 3 x 11 x 11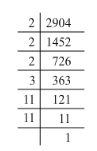
Grouping the factors into pairs:
2904 = (2 x 2) x (11 x 11) x 2 x 3
Here, the factors 2 and 3 do not occur in pairs. To be a perfect square, all the factors have to be in pairs. Hence, the smallest number by which 2904 must be divided for it to be a perfect square is 2 x 3, i.e. 6.
Question 5:Which of the following numbers are perfect squares?
11, 12, 16, 32, 36, 50, 64, 79, 81, 111, 121
Answer 5:
11: The perfect squares closest to 11 are 9 (9 = 32) and 16 (16 = 42). Since 3 and 4 are consecutive numbers, there are no perfect squares between 9 and 16, which means that 11 is not a perfect square.
12: The perfect squares closest to 12 are 9 (9 =32) and 16 (16 = 42). Since 3 and 4 are consecutive numbers, there are no perfect squares between 9 and 16, which means that 12 is not a perfect square.
16 = 42
32: The perfect squares closest to 32 are 25 (25 = 52) and 36 (36 = 62). Since 5 and 6 are consecutive numbers, there are no perfect squares between 25 and 36, which means that 32 is not a perfect square.
36 = 62
50: The perfect squares closest to 50 are 49 (49 = 72) and 64 (64 = 82). Since 7 and 8 are consecutive numbers, there are no perfect squares between 49 and 64, which means that 50 is not a perfect square.
64 = 82
79: The perfect squares closest to 79 are 64 (64 = 82) and 81 (81 = 92). Since 8 and 9 are consecutive numbers, there are no perfect squares between 64 and 81, which means that 79 is not a perfect square.
81 = 92
111: The perfect squares closest to 111 are 100 (100 = 102) and 121 (121 = 112). Since 10 and 11 are consecutive numbers, there are no perfect squares between 100 and 121, which means that 111 is not a perfect square.
121 = 112.
Question 6:Using prime factorization method, find which of the following numbers are perfect squares?
189, 225, 2048, 343, 441, 2916, 11025, 3549
Answer 6:
(i) 189 = 3 x 3 x 3 x 7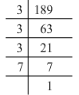
Grouping them into pairs of equal factors:
189 = (3 x 3) x 3 x 7
The factors 3 and 7 cannot be paired. Hence, 189 is not a perfect square.
(ii) 225 = 3 x 3 x 5 x 5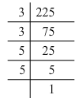
Grouping them into pairs of equal factors:
225 = (3 x 3) x (5 x 5)
There are no left out of pairs. Hence, 225 is a perfect square.
(iii) 2048 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2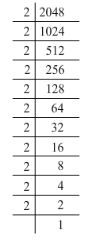
Grouping them into pairs of equal factors:
2048 = (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2) x 2
The last factor, 2 cannot be paired. Hence, 2048 is not a perfect square.
(iv) 343 = 7 x 7 x 7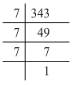
Grouping them into pairs of equal factors:
343 = (7 x 7) x 7
The last factor, 7 cannot be paired. Hence, 343 is not a perfect square.
(v) 441 = 3 x 3 x 7 x 7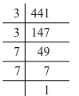
Grouping them into pairs of equal factors:
441 = (3 x 3) x (7 x 7)
There are no left out of pairs. Hence, 441 is a perfect square.
(vi) 2916 = 2 x 2 x 3 x 3 x 3 x 3 x 3 x 3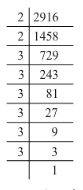
Grouping them into pairs of equal factors:
2916 = (2 x 2) x (3 x 3) x (3 x 3) x (3 x 3)
There are no left out of pairs. Hence, 2916 is a perfect square.
(vii) 11025 = 3 x 3 x 5 x 5 x 7 x 7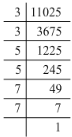
Grouping them into pairs of equal factors:
11025 = (3 x 3) x (5 x 5) x (7 x 7)
There are no left out of pairs. Hence, 11025 is a perfect square.
(viii) 3549 = 3 x 7 x 13 x 13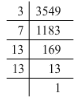
Grouping them into pairs of equal factors:
3549 = (13 x 13) x 3 x 7
The last factors, 3 and 7 cannot be paired. Hence, 3549 is not a perfect square.
Hence, the perfect squares are 225, 441, 2916 and 11025.
FAQs on Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 1, Class 8 Math RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the formula to find the square of a number? |  |
| 2. How do you find the square root of a number? |  |
| 3. Can negative numbers have square roots? |  |
| 4. Is 0 a perfect square? |  |
| 5. How can squares and square roots be applied in real-life situations? |  |
















