Chapter 9 - Linear Equation in One Variable (Part - 3), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 9.17:
Question 1:
Solve the following equation and verify your answer: 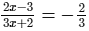
ANSWER:
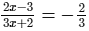
or 6x−9 = −6x−4 (After cross multiplication)
or 6x + 6x = −4 + 9
or x = 5/12
∴ x = 5/12
is the solution of the given equation.Check:
L.H.S. = 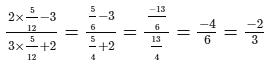
R.H.S. = −2/3
∴ L.H.S. = R.H.S. for x = 5/12
PAGE NO 9.17:
Question 2:
Solve the following equation and verify your answer: 
ANSWER:

or 10−5y = 3y + 21 (After cross multiplication)
or 3y + 5y = 10−21
or 8y = −11
or y = −11/8
∴ y = −11/8 is the solution of the given equation.
Check:Substituting y = −11/8 in the given equation, we get:
L.H.S. = 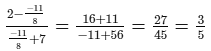
R.H.S. = 3/5
∴ L.H.S. = R.H.S. for y = −11/8
PAGE NO 9.17:
Question 3:
Solve the following equation and verify your answer: 
ANSWER:

or 6x = 5x−7 (After cross multiplication)
or 6x−5x = −7
or x = −7
∴ x = −7 is the solution of given equation.
Check:Substituting x = −7 in the given equation, we get:
L.H.S = 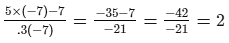
R.H.S. = 2
∴ L.H.S. = R.H.S. for x = −7.
PAGE NO 9.17:
Question 4:
Solve the following equation and verify your answer: 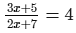
ANSWER:
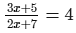
or 3x + 5 = 8x + 28
or 8x + 28 = 3x + 5 (After cross multiplication)
or8x−3x = 5−28
or 5x = −23
or x = −23/5
∴ x = −23/5 is the solution of given equation.
Check:Substituting x = −23/5 in the given equation, we get:
L.H.S. =
R.H.S. = 4
∴ L.H.S. = R.H.S. for x = −23/5
PAGE NO 9.17:
Question 5:
Solve the following equation and verify your answer: 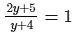
ANSWER:
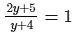
or 2y + 5 = y + 4
or 2y−y = 4−5or y = −1
Thus, y = −1 is the solution of the given equation.
Check:Substituting y = −1 in the given equation, we get:
L.H.S. = 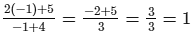
R.H.S. = 1
∴ L.H.S. = R.H.S. for y = −1.
PAGE NO 9.17:
Question 6:
Solve the following equation and verify your answer: 
ANSWER:

or 18x + 9 = 15x−10 [After cross multiplication]
or 18x−15x = −10−9
or 3x = −19
or x = −19/3
Thus, x = −19/3 is the solution of the given equation.
Check:Substituting x = −19/3 in the given equation, we get:
L.H.S. = 
R.H.S. = 5/9
∴ L.H.S. = R.H.S. for x = −19/3
PAGE NO 9.17:
Question 7:
Solve the following equation and verify your answer: 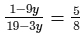
ANSWER:
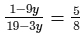
or 8−72y = 95−15y [After cross multiplication]
or 95−15y = 8−72y
or 72y−15y = 8−95
or 57y = −87
or y = −87/57
or y = −29/19
Thus y = −29/19 is the solution of the given equation.
Check:Substituting y = −29/19 in the given equation, we get:
L.H.S. = 
R.H.S. = 5/8
∴ L.H.S. = R.H.S. for y = −29/19
PAGE NO 9.17:
Question 8:
Solve the following equation and verify your answer: 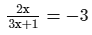
ANSWER:
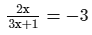
or 2x = −9x−3 [After cross multiplication]
or 2x + 9x = −3
or 11x = −3
or x = −3/11
Thus, x = −3/11 is the solution of the given equation.
Check:Substituting x = −3/11 in the given equation, we get:
L.H.S. =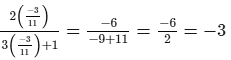
R.H.S. = −3
∴ L.H.S. = R.H.S. for x = −3/11
PAGE NO 9.17:
Question 9:
Solve the following equation and verify your answer: 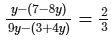
ANSWER:
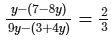
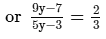
or 27y−21 = 10y−6 [After cross multiplication]
or 27y−10y = −6 + 21
or 17y = 15
or y = 15/17
Thus, y = 1517 is the solution of the given equation.
Check:Substituting y = 15/17 in the given equation, we get:
L.H.S. = 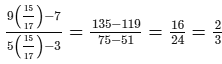
R.H.S. = 2/3
∴ L.H.S. = R.H.S. for y = 15/17
PAGE NO 9.17:
Question 10:
Solve the following equation and verify your answer: 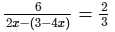
ANSWER:
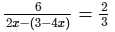
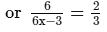
or 12x−6 = 18 [After cross multiplication]
or 12x = 18 + 6
or x = 24/12
or x = 2
Thus, x = 2 is the solution of the given equation.
Check:Substituting x = 2 in the given equation, we get:
L.H.S. = 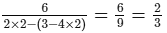
R.H.S. = 2/3
∴ L.H.S. = R.H.S. for x = 2.
PAGE NO 9.17:
Question 11:
Solve the following equation and verify your answer: 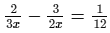
ANSWER:
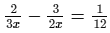

or, x = −10 [After cross multiplication]
Thus, x = −10 is the solution of the given equation.
Check:Substituting x = −10 in the given equation, we get:
L.H.S. = 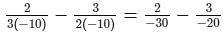

R.H.S. = 1/12
∴ L.H.S. = R.H.S. for x = −10.
PAGE NO 9.17:
Question 12:
Solve the following equation and verify your answer: 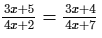
ANSWER:
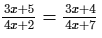
or, 12x2 + 20x + 21x + 35 = 12x2 + 16x + 6x + 8 [Cross multiply]
or, 12x2−12x2 + 41x−22x = 8−35
or, 19x = −27
or, x = −27/19
Thus, x = −27/19 is the solution of the given equation
Check:Substituting x = −27/19 in the given equation, we get:
L.H.S. =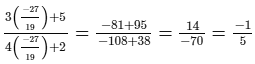
R.H.S. =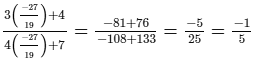
∴ L.H.S. = R.H.S. for x = −27/19
PAGE NO 9.17:
Question 13:
Solve the following equation and verify your answer: 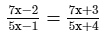
ANSWER:
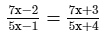
or 35x2 + 28x−10x−8 = 35x2 + 15x−7x−3 [After cross multiplication]
or 35x2−35x2 + 18x−8x = −3 + 8
or 10x = 5
or x = 5/10
or x = 1/2
Thus, x = 1/2 is the solution of the given equation.
Check:Substituting x = 1/2 in the given equation, we get:
L.H.S. =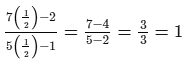
R.H.S. = 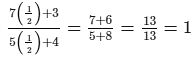
∴ L.H.S. = R.H.S. for x = 1/2
PAGE NO 9.17:
Question 14:
Solve the following equation and verify your answer: 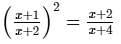
ANSWER:
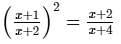
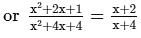
or x3 + 2x2 + x + 4x2 + 8x + 4
= x3 + 4x2 + 4x + 2x2 + 8x + 8 [After cross multiplication]
or x3−x3 + 6x2−6x2 + 9x−12x = 8−4
or −3x = 4
or x = 4/−3 = −4/3
Thus, x = −4/3 is the solution of the given equation.
Check:Substituting x = −4/3 in the given equation, we get:
L.H.S. =
R.H.S. = 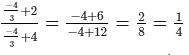
∴ L.H.S. = R.H.S. for x = −4/3
PAGE NO 9.17:
Question 15:
Solve the following equation and verify your answer: 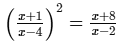
ANSWER:
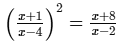
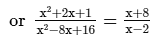 [(a + b)2 = a2 + b2 + 2ab and (a−b)2 = a2 + b2−2ab ]
[(a + b)2 = a2 + b2 + 2ab and (a−b)2 = a2 + b2−2ab ]
or x3 + 2x2 + x−2x2−4x−2 = x3−8x2 + 16x + 8x2−64x + 128 [After cross multiplication]
or x3−x3−3x + 48x = 128 + 2
or 45x = 130
or x = 130/45 = 26/9
Thus x = 26/9 is the solution of the given equation.
Check:Substituting x = 26/9 in the given equation, we get:
L.H.S. = 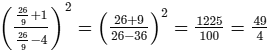
R.H.S. = 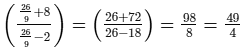
∴ L.H.S. = R.H.S. for x = 26/9
PAGE NO 9.17:
Question 16:
Solve the following equation and verify your answer: 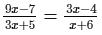
ANSWER:
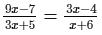
or 9x2−7x + 54x−42 = 9x2−12x + 15x−20 [After cross multiplication]
or 9x2−9x2 + 47x−3x = −20 + 42
or 44x = 22
or x = 22/44
or x = 1/2
Thus, x = 1/2 is the solution of the given equation.
Check:Substituting x = 1/2 in the given equation, we get:
L.H.S. = 
R.H.S. = 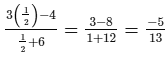
∴ L.H.S. = R.H.S. for x = 1/2
PAGE NO 9.17:
Question 17:
Solve the following equation and verify your answer: 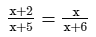
ANSWER:
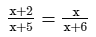
or x2 + 2x + 6x + 12 = x2 + 5x [After cross multiplication]
or x2−x2 + 8x−5x = −12
or 3x = −12
or x = −12/3
or x = −4
Thus, x = −4 is the solution of given equation.
Check:Substituting x = −4 in the given equation, we get:
L.H.S. = 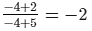
R.H.S. = 
∴ L.H.S. = R.H.S. for x = −4.
PAGE NO 9.17:
Question 18:
Solve the following equation and verify your answer: 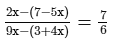
ANSWER:
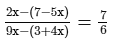
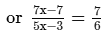
or 42x−42 = 35x−21 [After cross multiplication]
or 42x−35x = −21 + 42
or 7x = 21
or x = 21/7
or x = 3
Thus, x = 3 is the solution of the given equation.
Check:Substituting x = 3 in the given equation, we get:
L.H.S. =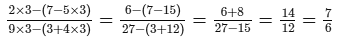
R.H.S. = 7/6
∴ L.H.S. = R.H.S. for x = 3.
PAGE NO 9.17:
Question 19:
Solve the following equation and verify your answer: 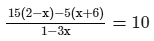
ANSWER:
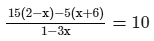
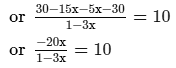
or 10−30x = −20x [After cross multiplication]
or −20x + 30x = 10
or 10x = 10
or x = 1
Thus, x = 1 is the solution of the given equation.
Check:Substituting x = 1 in the given equation, we get:
L.H.S. = 
R.H.S. = 10
∴ L.H.S. = R.H.S. for x = 1.
PAGE NO 9.17:
Question 20:
Solve the following equation and verify your answer: 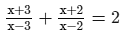
ANSWER:
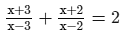
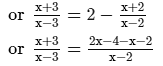
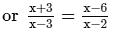
or x2−2x + 3x−6 = x2−3x−6x + 18 [After cross multiplication]
or x2−x2 + x + 9x = 18 + 6
or 10x = 24
or x = 24/10
or x = 12/5
Thus, x = 12/5 is the solution of the given equation.
Check:Substituting x = 12/5 in the given equation, we get:
L.H.S. =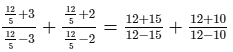
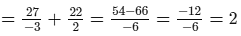
R.H.S. = 2
∴ L.H.S. = R.H.S. for x = 12/5
PAGE NO 9.17:
Question 21:
Solve the following equation and verify your answer: 
ANSWER:

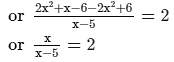
or 2x−10 = x [After cross multiplication]
or 2x−x = 10or x = 10
Thus, x = 10 is the solution of the given equation.
Check:Substituting x = 10 in the given equation, we get:
L.H.S. = 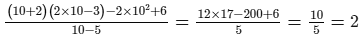
R.H.S. = 2
∴ L.H.S. = R.H.S. for x = 10.
PAGE NO 9.17:
Question 22:
Solve the following equation and verify your answer: 
ANSWER:

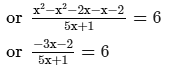
or 30x + 6 = −3x−2 [After cross multiplication]or 30x + 3x = −2−6
or 33x = −8
or x = −8/33
Thus, x = −8/33 is the solution of the given equation.
Check:Substituting x = −8/33 in the given equation, we get:
L.H.S. =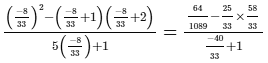
 = R.H.S. = 6
= R.H.S. = 6
∴ L.H.S. = R.H.S. for x = −8/33
PAGE NO 9.17:
Question 23:
Solve the following equation and verify your answer: 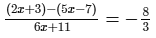
ANSWER:
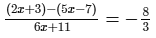
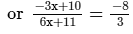
or −9x + 30 = −48x−88 [After cross multiplication]
or −9x + 48x = −88−30
or 39x = −118
or x = −118/39
Thus, x = −118/39 is the solution of the given equation.
Check:Substituting x = −118/39 in the given equation, we get:
L.H.S. = 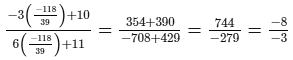
R.H.S. = −83
∴ L.H.S. = R.H.S. for x = −118/39
PAGE NO 9.17:
Question 24:
Find a positive value of x for which the given equation is satisfied:
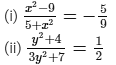
ANSWER:
(i) 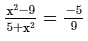
or 9x2−81 = −25 − 5x2 [After cross multiplication]
or 9x2 + 5x2 = −25 + 81
or 14x2 = 56
or x2 = 56/14
or x2 = 4 = 22
or x = 2
Thus, x = 2 is the solution of the given equation.
Check:Substituting x = 2 in the given equation, we get:
L.H.S.= 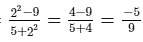 R.H.S.=−5/9
R.H.S.=−5/9
∴ L.H.S.=R.H.S. for x=2.
(ii) 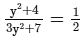
or 3y2+7 = 2y2+8 [After cross multiplication]
or 3y2−2y2 = 8−7
or y2 = 1
or y = 1
Thus, y = 1 is the solution of the given equation.
Check:Substituting y = 1 in the given equation, we get:
L.H.S. = 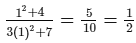
R.H.S .= 1/2
∴ L.H.S. = R.H.S. for y = 1.
FAQs on Chapter 9 - Linear Equation in One Variable (Part - 3), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is a linear equation in one variable? |  |
| 2. How do you solve a linear equation in one variable? |  |
| 3. Can a linear equation in one variable have more than one solution? |  |
| 4. What is the importance of linear equations in one variable in real life? |  |
| 5. Can all equations be classified as linear equations in one variable? |  |

|
Explore Courses for Class 8 exam
|

|

















