Class 9 Exam > Class 9 Notes > RD Sharma Solutions for Class 9 Mathematics > RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths
RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. Express the following rational numbers as decimals:
(i) 42/100
(ii) 327/500
(iii) 15/4
Solution:
(i) By long division method
100) 
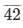( 0.42
400
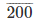
200
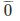
Therefore, 42/100 = 0.42
(ii) By long division method
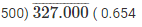
3000
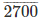
2500
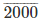
2000
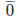
Therefore, 327/500 = 0.654
(iii) By long division method
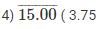
12
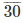
28
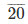
20
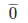
Therefore, 15/4 = 3.75
Q2. Express the following rational numbers as decimals:
(i) 2/3
(ii)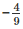 
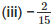
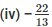
(v) 437/999
Solution:
(i) By long division method
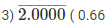
18
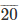
18
Therefore, 2/3 = 0.66
(ii) By long division method
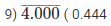
3600
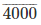
3600
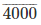
3600
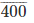
Therefore,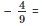 
– 0.444
(iii) By long division method
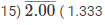
15
45
45
45
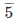
Therefore, 2/15 = -1.333
(iv) By long division method
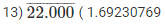
13
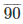
78
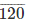
117
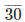
26
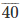
39
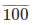
91
78
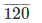
117
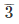
Therefore,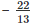 
= – 1.69230769
(v) By long division method
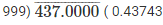
3996
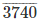
2997
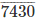
6993
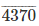
3996
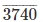
2997
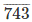
Therefore, 437/999 = 0.43743
Q3. Look at several examples of rational numbers in the form of p/q (q ≠ 0), where p and q are integers with no common factor other than 1 and having terminating decimal representations. Can you guess what property q must satisfy?
Solution: A rational number p/q is a terminating decimal only, when prime factors of q are q and 5 only. Therefore, p/q is a terminating decimal only, when prime factorization of q must have only powers of 2 or 5 or both.
The document RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics is a part of the Class 9 Course RD Sharma Solutions for Class 9 Mathematics.
All you need of Class 9 at this link: Class 9
FAQs on RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are RD Sharma Solutions? |  |
Ans. RD Sharma Solutions are comprehensive solutions to the math textbook authored by R.D. Sharma. These solutions provide step-by-step explanations and solutions to the questions and exercises in the textbook, helping students understand and solve math problems effectively.
| 2. What is Ex-1.2 in RD Sharma Solutions for Class 9? | |
Ans. Ex-1.2 in RD Sharma Solutions for Class 9 refers to Exercise 1.2 in the textbook. This exercise is part of the Number System chapter and covers various topics related to number systems such as integers, rational numbers, irrational numbers, etc. The solutions provided for Ex-1.2 help students practice and understand these concepts better.
| 3. How can RD Sharma Solutions for Class 9 be beneficial for exam preparation? | |
Ans. RD Sharma Solutions for Class 9 are highly beneficial for exam preparation as they provide detailed explanations and step-by-step solutions for each question in the textbook. By practicing these solutions, students can improve their problem-solving skills, understand the concepts better, and gain confidence for the exams.
| 4. Are RD Sharma Solutions for Class 9 available in the same language as the article title? | |
Ans. Yes, RD Sharma Solutions for Class 9 are available in the same language as the article title. These solutions are designed to cater to students studying in schools where the medium of instruction is the same language as mentioned in the article title. This ensures that students can easily understand and grasp the concepts explained in the solutions.
| 5. Can the RD Sharma Solutions for Class 9 help in improving overall math skills? | |
Ans. Yes, RD Sharma Solutions for Class 9 can definitely help in improving overall math skills. The solutions provided in these books not only focus on solving the textbook questions but also provide additional practice exercises and problem-solving techniques. By consistently practicing these solutions, students can enhance their mathematical reasoning, logical thinking, and problem-solving abilities, which are essential for excelling in mathematics.
Related Exams
About this Document
|
1.5K Views |
|
4.81/5 Rating |
|
Dec 23, 2024 Last updated |
Document Description: RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths for Class 9 2024 is part of RD Sharma Solutions for Class 9 Mathematics preparation.
The notes and questions for RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths have been prepared according to the Class 9 exam syllabus. Information about RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths covers topics
like and RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths Example, for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths.
Introduction of RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths in English is available as part of our RD Sharma Solutions for Class 9 Mathematics
for Class 9 & RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths in Hindi for RD Sharma Solutions for Class 9 Mathematics course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics
Description
Full syllabus notes, lecture & questions for RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics - Class 9 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 9 Mathematics | Best notes, free PDF download
Information about RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths
In this doc you can find the meaning of RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths defined & explained in the simplest way possible. Besides explaining types of
RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths tests, examples and also practice Class 9
tests
|
Explore Courses for Class 9 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
ppt
,Maths | RD Sharma Solutions for Class 9 Mathematics
,Class 9
,Viva Questions
,Extra Questions
,Previous Year Questions with Solutions
,practice quizzes
,Important questions
,shortcuts and tricks
,Number System
,RD Sharma Solutions Ex-1.2
,Summary
,Number System
,study material
,mock tests for examination
,Maths | RD Sharma Solutions for Class 9 Mathematics
,Sample Paper
,Class 9
,Maths | RD Sharma Solutions for Class 9 Mathematics
,Class 9
,Semester Notes
,Number System
,Exam
,MCQs
,RD Sharma Solutions Ex-1.2
,Objective type Questions
,Free
,video lectures
,RD Sharma Solutions Ex-1.2
,past year papers
;
Additional Information about RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths for Class 9 Preparation
RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths Free PDF Download
The RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths now and kickstart your journey towards success in the Class 9 exam.
Importance of RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths
The importance of RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths Notes
RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths Notes on EduRev are your ultimate resource for success.
RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths Class 9 Questions
The "RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths on the App
Students of Class 9 can study RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of RD Sharma Solutions Ex-1.2, Number System, Class 9, Maths is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup