Ex-10.3, Congruent Triangles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q. (1) In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the other. Prove that the triangles are congruent.
Solution:
Given that, in two right triangles one side and acute angle of one are equal to the corresponding side and angles of the other.
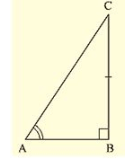

We have to prove that the triangles are congruent.
Let us consider two right triangles such that
∠ B = ∠ C = 90∘ …….(i)
AB = DE …….(ii)
∠ C = ∠ F From(iii)
Now observe the two triangles ABC and DEF
∠ C = ∠ F [From (iii)]
∠ B = ∠ E [From (i)]
and AB = DE [From (ii)]
So, by AAS congruence criterion, we have Δ ABC ≅ Δ DEF
Therefore, the two triangles are congruent
Hence proved
Q. (2) If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
Solution:
Given that the bisector of the exterior vertical angle of a triangle is parallel to the base and we have to prove that the triangle is isosceles. Let ABC be a triangle such that AD is the angular bisector of exterior vertical angle EAC and AD ∥ BC
Let ∠ EAD = (i), ∠ DAC = (ii), ∠ ABC = (iii) and ∠ ACB = (iv)
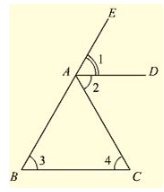
We have,
(i) = (ii) [AD is a bisector of ∠ EAC]
(i) = (iii) [Corresponding angles]
and (ii) = (iv) [alternative angle]
(iii) = (iv)
- AB = AC
Since, in Δ ABC, two sides AB and AC are equal we can say that Δ ABC is isosceles triangle.
Q. (3) In an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
Solution:
Let Δ ABC be isosceles such that AB = AC.
- ∠ B = ∠ C
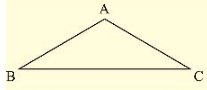
Given that vertex angle A is twice the sum of the base angles B and C. i.e., ∠ A = 2(∠ B + ∠ C)
∠ A = 2(∠ B + ∠ B)
∠ A = 2(2 ∠ B)
∠ A = 4(∠ B)
Now, We know that sum of angles in a triangle = 180°
∠ A + ∠ B + ∠ C = 180°
4 ∠ B + ∠ B + ∠ B = 180°
6 ∠ B = 180°
∠ B = 30°
Since, ∠ B = ∠ C
- ∠ B = ∠ C = 30°
And ∠ A = 4 ∠ B
- ∠ A = 4 x 30° = 120°
Therefore, angles of the given triangle are 120°, 30° and 30°.
= 428 and LB = LC]
Q. (4) PQR is a triangle in which PQ = PR and is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
Solution : Given that PQR is a triangle such that PQ = PR ant S is any point on the side PQ and ST ∥ QR.
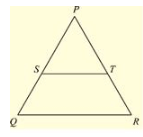
To prove,
PS = PT
Since, PQ = PR
- PQR is an isosceles triangle.
- ∠ Q = ∠ R (or) ∠ PQR = ∠ PRQ
Now, ∠ PST = ∠ PQR and ∠ PTS = ∠ PRQ [Corresponding angles as ST parallel to QR]
Since, ∠ PQR = ∠ PRQ
- ∠ PST = ∠ PTS
Now, In Δ PST, ∠ PST = ∠ PTS
Δ PST is an isosceles triangle
Therefore, PS = PT
Q. (5) In a Δ ABC, it is given that AB = AC and the bisectors of B and C intersect at O. If M is a point on BO produced, prove that ∠ MOC = ∠ ABC.
Solution:
Given that in Δ ABC,
AB = AC and the bisector of ∠ B and ∠ C intersect at O. If M is a point on BO produced
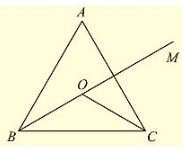
We have to prove ∠ MOC = ∠ ABC
Since,
AB = AC
- ABC is isosceles
- ∠ B = ∠ C (or)
- ∠ ABC = ∠ ACB
Now,
BO and CO are bisectors of ∠ ABC and ∠ ACB respectively
= > ABO = ∠ OBC = ∠ ACO = ∠ OCB = 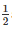 ∠ ABC =
∠ ABC = 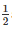 ∠ ACB ……(i)
∠ ACB ……(i)
We have, in Δ OBC
∠ OBC + ∠ OCB + ∠ BOC = 180° ……(ii)
And also
∠ BOC + ∠ COM = 180° ……(iii) [Straight angle]
Equating (ii) and (iii)
- ∠ OBC + ∠ OCB + ∠ BOC = ∠ BOC + ∠ MOC
- ∠ OBC + ∠ OCB = ∠ MOC [From (i)]
- 2 ∠ OBC = ∠ MOC [From (i)]
- 2 (
 ∠ ABC) = ∠ MOC [From (i)]
∠ ABC) = ∠ MOC [From (i)] - ∠ ABC = ∠ MOC
Therefore, ∠ MOC = ∠ ABC
Q. (6) P is a point on the bisector of an angle ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
Sol:
Given that P is a point on the bisector of an angle ABC, and PQ ∥ AB.
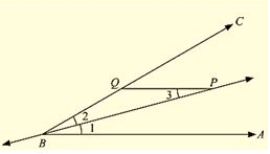
We have to prove that Δ BPQ is isosceles.
Since,
BP is bisector of ∠ ABC = ∠ ABP = ∠ PBC ……(i)
Now,
PQ ∥ AB
- ∠ BPQ = ∠ ABP ……(ii) [alternative angles]
From (i) and (ii), we get
∠ BPQ = ∠ PBC (or) ∠ BPQ = ∠ PBQ
Now,
In BPQ,
∠ BPQ = ∠ PBQ
Δ BPQ is an isosceles triangle.
Hence proved
Q. (7) Prove that each angle of an equilateral triangle is 60°.
Sol:
Given to prove each angle of an equilateral triangle is 60°.
Let us consider an equilateral triangle ABC.
Such that AB = BC = CA
Now, AB = BC
- ∠ A = ∠ C ……(i) [Opposite angles to equal sides are equal]
And BC = AC
- ∠ B = ∠ A ……(ii)
From (i) and (ii), we get
∠ A = ∠ B = ∠ C ……(iii)
We know that
Sum of angles in a triangle = 180
- ∠ A + ∠ B + ∠ C = 180
- ∠ A + ∠ A + ∠ A = 180
- 3 ∠ A = 180
- ∠ A = 60
∠ A = ∠ B = ∠ C = 60
Hence, each angle of an equilateral triangle is 60°.
Q. (8) Angles Δ A, B, C of a triangle ABC are equal to each other. Prove that ABC is equilateral.
Sol:
Given that angles A, B, C of a triangle ABC equal to each other.
We have to prove that Δ ABC is equilateral
We have, ∠ A = ∠ B = ∠ C
Now,
∠ A = ∠ B
- BC = AC [opposite sides to equal angles are equal]
And ∠ B = ∠ C
- AC = AB
From the above we get
AB = BC = AC
- Δ ABC is equilateral.
Q. (9) ABC is a triangle in which ∠ B = 2 ∠ C. D is a point on BC such that AD bisects ∠ BAC and AB = CD. Prove that [∠ BAC = 72 .
Solution: Given that in ABC, ∠ B = 2 ∠ C and D is a point on BC such that AD bisectors ∠ BAC and
AB = CD.
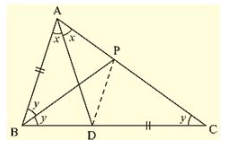
We have to prove that ∠ BAC = 72°
Now, draw the angular bisector of ∠ ABC, which meets AC in P.
Join PD
Let C = ∠ ACB = y
- ∠ B = ∠ ABC = 2 ∠ C = 2y and also
- Let ∠ BAD = ∠ DAC
- ∠ BAC = 2x [ AD is the bisector of ∠ BAC ]
Now, in Δ BPC,
- ∠ CBP = y [BP is the bisector of ∠ ABC ]
- ∠ PCB = y
- ∠ CBP = ∠ PCB = y [PC = BP]
Consider, Δ ABP and Δ DCP, we have
Δ ABP = Δ DCP = y
AB = DC [Given]
And PC = BP [From above]
So, by SAS congruence criterion, we have ΔABP≅ΔDCP
Now,
∠ BAP = ∠ CDF and AP = DP [Corresponding parts of congruent triangles are equal]
- ∠ BAP = ∠ CDP = 2
Consider, Δ APD,
We have AP = DP
= ∠ ADP = ∠ DAP
But ∠ DAP = x
- ∠ ADP = ∠ DAP = x
Now
In Δ ABD.
∠ ABD + ∠ BAD + ∠ ADB = 180
And also ∠ ADB + ∠ ADC = 180° [Straight angle]
From the above two equations, we get
∠ ABD + ∠ BAD + ∠ ADB = ∠ ADB + ∠ ADC
- 2y + x = ∠ ADP + ∠ PDC
- 2y + x = x + 2x
- 2y = 2x
- y = x (or) x = y
We know,
Sum of angles in a triangle = 180°
So, In Δ ABC,
- ∠ A + ∠ B + ∠ C = 180°
- 2x + 2y + y = 180° [∠ A = 2x, ∠ B = 2y, ∠ C = y]
- 2(y)+3y = 180° [x = y]
- 5y = 180°
- y = 36°
Now, ∠ A = ∠ BAC = 2 x 36° = 72°
Q. (10) ABC is a right angled triangle in which ∠ A = 90° and AB = AC. Find ∠ B and ∠ C.
Solution: Given that ABC is a right angled triangle such that ∠ A = 90° and AB = AC
Since, AB = AC
- Δ ABC is also isosceles.
Therefore, we can say that Δ ABC is right angled isosceles triangle.
- ∠ C = ∠ B and ∠ A = 90° ……(i)
Now, we have sum of angled in a triangle = 180°
- ∠ A + ∠ B + ∠ C = 180°
- 90° + ∠ B + ∠ B = 180° [From(i)]
- 2∠ B = 180° – 90°
- ∠ B = 45°
Therefore, ∠ B = ∠ C = 45°
FAQs on Ex-10.3, Congruent Triangles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What are congruent triangles? |  |
| 2. How do you prove two triangles congruent? |  |
| 3. What is the importance of congruent triangles in mathematics? |  |
| 4. How can congruent triangles be used to solve problems? |  |
| 5. Can congruent triangles have different orientations? |  |

|
Explore Courses for Class 9 exam
|

|

















