Ex-10.5, Congruent Triangles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q. (1) ABC is a triangle and D is the mid-point of BC. The perpendiculars from B to AB and AC are equal. Prove that the triangle is isosceles.
Sol:
Given that, in two right triangles one side and acute angle of one are equal to the corresponding side and angle of the other
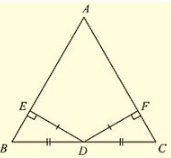
We have to prove that the triangles are congruent
Let us consider two right triangles such that
∠ B = ∠ E = 90 ……(i)
AB = DE…… (ii)
∠ C = ∠ F……(iii)
Now observe the two triangles ABC and DEF
∠ C = ∠ F[From (iii)]
∠ B = ∠ E [From (i)]
And AB = DE[From (ii)]
So, by AAS congruence criterion, we have
ΔABC≅ΔDEF
Therefore, the two triangles are congruent
Hence proved
Q. (2) ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that Δ ABC is isosceles
Sol: Given that ABC is a triangle in which BE and CF are perpendicular to the sides AC and AS respectively such that BE = CF.
To prove, Δ ABC is isosceles
Now, consider Δ BCF and Δ CBE,
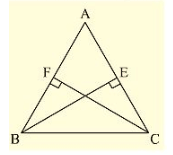
We have
∠ BFC = CEB = 90 [Given]
BC = CB[Common side]
And CF = BE[Given]
So, by RHS congruence criterion, we have
ΔBFC≅ΔCEB
Now,
∠ FBC = ∠ EBC [Incongruent triangles corresponding parts are equal]
∠ ABC = ∠ ACB
AC = AB[Opposite sides to equal angles are equal in a triangle]
Δ ABC is isosceles
Q. (3) If perpendiculars from any point within an angle on its arms are congruent. Prove that it lies on the bisector of that angle.
Solution:
Given that, if perpendicular from any point within, an angle on its arms is congruent, prove that it lies on the bisector of that angle.
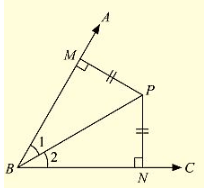
Now,
Let us consider an angle ABC and let BP be one of the arm within the angle
Draw perpendicular PN and PM on the arms BC and BA such that they meet BC and BA in N and M respectively.
Now, in Δ BPM and Δ BPN
We have ∠ BMP = ∠ BNP = 90° [given]
BP = BP[Common side]
And MP = NP[given]
So, by RHS congruence criterion, we have
ΔBPM≅ΔBPN
Now, ∠ MBP = ∠ NBP [Corresponding parts of congruent triangles we equal]
- BP is the angular bisector of ∠ABC.
Hence proved
Q. (4) In fig. (10).99, AD ⊥ CD and CB ⊥ CD. If AQ = BP and DP = CQ, prove that ∠ DAQ = ∠ CBP.
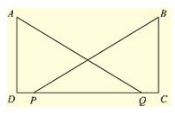
Sol:
Given in the fig. (10).99, AD ⊥ CD and CB ⊥ CD.
And AQ = BP and DP = CQ,
To prove that ∠ DAQ = ∠ CBP
Given that DP = QC
Add PQ on both sides
- DP + PQ = PQ + QC
- DQ = PC ……(i)
Now, consider triangle DAQ and CBP,
We have
∠ ADQ = ∠ BCP = 90° [given] AQ = BP [given]
And DQ = PC[From (i)]
So, by RHS congruence criterion, we have
ΔDAQ≅ΔCBP
Now,
∠ DAQ = ∠ CBP [Corresponding parts of congruent triangles are equal]
Hence proved
Q. (5) ABCD is a square, X and Y are points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠ BAY = ∠ ABX.
Solution:
Given that ABCD is a square, X and Y are points on sides AD and BC respectively such that AY = BX.
To prove BY = AX and ∠ BAY = ∠ ABX
Join B and X, A and Y.
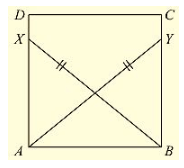
Since, ABCD is a square
- ∠ DAB = ∠ CBA = 90°
- ∠ XAB = ∠ YAB = 90° ……(i)
Now, consider triangle XAB and YBA
We have
∠ XAB = ∠ YBA = 90°. [From (i)] BX = AY[given]
And AB = BA[Common side]
So, by RHS congruence criterion, we have ΔXAB≅ΔYBA
Now, we know that corresponding parts of congruent triangles are equal.
BY = AX and ∠ BAY = ∠ ABX
Hence proved
Q. (6) Which of the following statements are true (T) and which are false (F):
(i) Sides opposite to equal angles of a triangle may be unequal.
(ii) Angles opposite to equal sides of a triangle are equal
(iii) The measure of each angle of an equilateral triangle is 60
(iv) If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
(v) The bisectors of two equal angles of a triangle are equal.
(vi) If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
(vii) The two altitudes corresponding to two equal sides of a triangle need not be equal.
(viii) If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
(ix) Two right-angled triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
Solution:
(i) False (F)
Reason: Sides opposite to equal angles of a triangle are equal
(ii) True (F)
Reason: Since the sides are equal, the corresponding opposite angles must be equal
(iii) True (T)
Reason: Since all the three angles of equilateral triangles are equal and sum of the three angles is 180 , each angle will be equal to 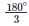 =60∘
=60∘
(iv) False (F)
Reason: Here the altitude from the vertex is also the perpendicular bisector of the opposite side.
The triangle must be isosceles and may be an equilateral triangle.
(v) True (T)
Reason: Since it an isosceles triangle, the lengths of bisectors of the two equal angles are equal
(vi) False (F)
Reason: The angular bisector of the vertex angle is also a median
⇒ The triangle must be an isosceles and also may be an equilateral triangle.
(vii) False (F)
Reason: Since two sides are equal, the triangle is an isosceles triangle. The two altitudes corresponding to two equal sides must be equal.
(viii) False (F)
Reason: The two right triangles may or may not be congruent
(ix) True (T)
Reason: According to RHS congruence criterion the given statement is true.
Q. (7) Fill the blanks In the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ___
(ii) Angle opposite to equal sides of a triangle are ___
(iii) In an equilateral triangle all angles are ___
(iv) In Δ ABC, if ∠ A = ∠ C, then AB =
(v) If altitudes CE and BF of a triangle ABC are equal, then AB ___
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is ___ CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC≅Δ ___
Solution:
(i) Sides opposite to equal angles of a triangle are equal
(ii) Angles opposite to equal sides of a triangle are equal
(iii) In an equilateral triangle all angles are equal Reason: Since all sides are equal in a equilateral triangle. the angles opposite to equal sides will be equal .
(iv) In a Δ ABC, if ∠ A = ∠ C, then AB = BC
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = AC
(vi) In an isosceles triangle Δ ABC with AB = AC, if BD and CE are its altitudes, then BD is equal to CE
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then, Δ ABC = Δ EFD.
FAQs on Ex-10.5, Congruent Triangles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What are congruent triangles? |  |
| 2. How do you prove two triangles are congruent? |  |
| 3. What is the importance of congruent triangles in geometry? |  |
| 4. Can you determine the congruence of triangles based on their angles alone? |  |
| 5. Are there any shortcuts or formulas to determine triangle congruence? |  |

|
Explore Courses for Class 9 exam
|

|












