RD Sharma Solutions Ex-11.1, Coordinate Geometry, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1) Plot the following points on the graph paper:
(i) (2,5)
(ii) (4,-3)
(iii) (-5,-7)
(iv) (7,-4)
(v) (-3,2)
(vi) (7,0)
(vii) (-4,0)
(viii) (0,7)
(ix) (0,-4)
(x) (0,0)
Solution:
The given points are,
A (2,5), B (4,-3), C (-5,-7), D (7,-4), E (-3,2),
F (7,0), G (-4,0), H (0,7), I (0,-4), J (0,0)
Let X ‘OX and Y ‘ OY be the coordinate axes.
(i) Here for the given point the abscissa is 2 units and ordinate is 5 units. The point is in the first quadrant. So it will look like as shown in the following figure.
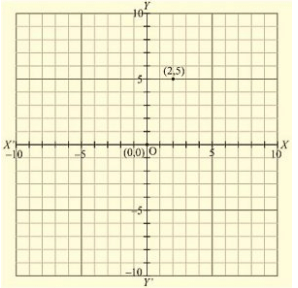
(ii) Here for the given point the abscissa is 4 units and ordinate is -3 units. The point is in the fourth quadrant. So it will look like as shown in the following figure.
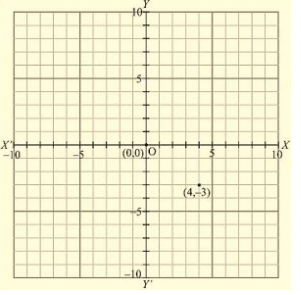
(iii) Here for the given point the abscissa is -5 units and ordinate is -7 units. The point is in the third quadrant. So it will look like as shown in the following figure.
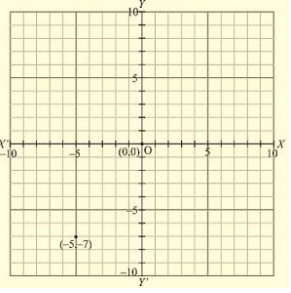
(iv) Here for the given point the abscissa is 7 units and ordinate is -4 units. The point is in the fourth quadrant. So it will look like as shown in the following figure.
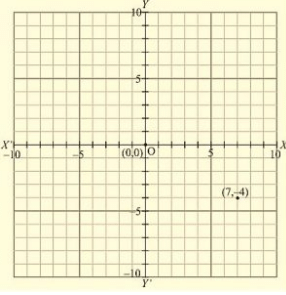
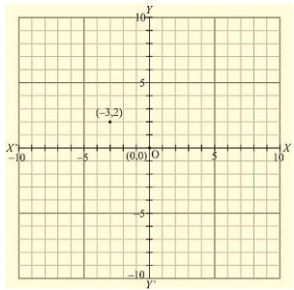
(v) Here for the given point the abscissa is -3 units and ordinate is 2 units. The point is in the second quadrant. So it will look like as shown in the following figure.
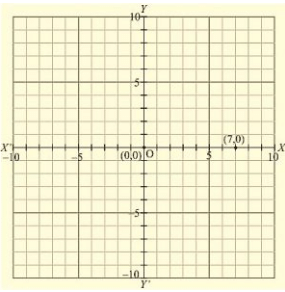
(vi) Here for the given point the abscissa is 7 units and ordinate is 0 units. The point is on the x-axis. So it will look like as shown in the following figure.
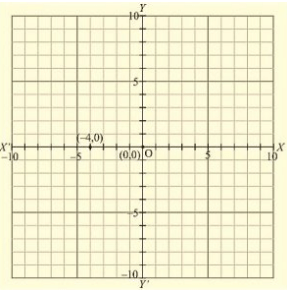
(vii) Here for the given point the abscissa is -4 units and ordinate is 0 units. The point is on the x-axis. So it will look like as shown in the following figure.
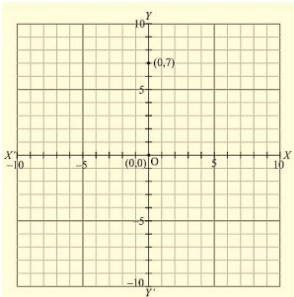
(viii) Here for the given point the abscissa is 0 units and ordinate is 7 units. The point is on the y-axis. So it will look like as shown in the following figure.
(ix) Here for the given point the abscissa is 0 units and ordinate is -4 units. The point is on the y-axis. So it will look like as shown in the following figure.
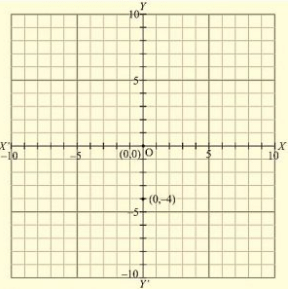
(x) Here for the given point the abscissa is 0 units and ordinate is 0 units.
The point is basically intersection of the coordinate axis. So it will look like as shown in the following figure.
Q.2) Write the coordinates of each of the following points marked in the graph paper.
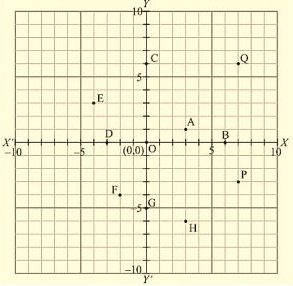
Solution:
A (3,1), B (6,0), C (0,6), D (-3,0), E (-4,3), F (-2,-4), G (0,-5), H (3,-6), P (7,-3), Q (7,6)
1) The distance of point A from y-axis is 3 units and that of from x-axis is 1 units. Since A lies in the first quadrant, so its coordinates are (3,1).
2) The distance of point B from y-axis is 6 units and that of from x-axis is 0 units. Since B lies on x-axis, so its coordinates are (6,0).
3) The distance of point C from y-axis is 0 units and that of from x-axis is 6 units. Since C lies on y-axis, so its coordinates are (0,6).
4) The distance of point D from y-axis is -3 units and that of from x-axis is 0 units. Since D lies on x-axis, so its coordinates are (-3,0).
5) The distance of point E from y-axis is -4 units and that of from x-axis is 3 units. Since E lies in the second quadrant, so its coordinates are (-4,3).
6) The distance of point F from y-axis is -2 units and that of from x-axis is -4 units. Since F lies in the third quadrant, so its coordinates are (-2,-4).
7) The distance of point G from y-axis is 0 units and that of from x-axis is -5 units. Since G lies on y-axis, so its coordinates are (0,-5).
8) The distance of point H from y-axis is 3 units and that of from x-axis is -6 units. Since H lies in the fourth quadrant, so its coordinates are (3,-6).
9) The distance of point P from y-axis is 7 units and that of from x-axis is -3 units. Since P lies in the fourth quadrant, so its coordinates are (7,-3).
10) The distance of point Q from y-axis is 7 units and that of from x-axis is 6 units. Since Q lies in the first quadrant, so its coordinates are (7,6).
FAQs on RD Sharma Solutions Ex-11.1, Coordinate Geometry, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of coordinate geometry in mathematics? |  |
| 2. How can coordinate geometry be used in real-life applications? |  |
| 3. What are the different types of coordinates used in coordinate geometry? |  |
| 4. How are equations of lines represented in coordinate geometry? |  |
| 5. How can coordinate geometry be used to calculate the distance between two points? |  |

|
Explore Courses for Class 9 exam
|

|

















