RD Sharma Solutions Ex-12.2, (Part -2), Heron's Formula, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q8. Find the area of the quadrilateral ABCD in which AD = 24 cm, angle BAD = 90∘ and BCD forms an equilateral triangle whose each side is equal to 26 cm. [Take √3 = 1.73]
Solution:
Given that, in a quadrilateral ABCD in which AD = 24 cm,
Angle BAD = 90∘
BCD is an equilateral triangle and the sides BC = CD = BD = 26 cm
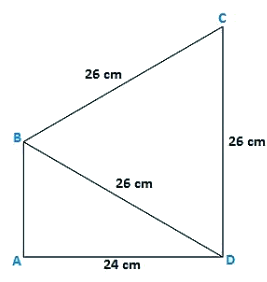
In triangle BAD, by applying Pythagoras theorem,
BA2 = BD2−AD2
BA2 = 262+242
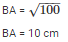
Area of the triangle 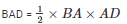
Area of the triangle 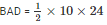
Area of the triangle BAD = 120 cm2
Area of the equilateral triangle 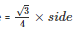
Area of the equilateral triangle QRS 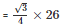
Area of the equilateral triangle BCD = 292.37 cm2
Therefore, the area of quadrilateral ABCD = area of triangle BAD + area of the triangle BCD
The area of quadrilateral ABCD = 120 + 292.37
= 412.37 cm2
Q9. Find the area of quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm and the diagonal BD = 20 cm.
Solution:
Given
AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm, and the diagonal
BD = 20 cm.
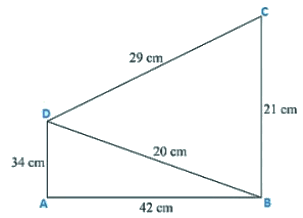
Now, for the area of triangle ABD
Perimeter of triangle ABD 2s = AB + BD + DA
2s = 34 cm + 42 cm + 20 cm
s = 48 cm/p>
By using Heron’s Formula,
Area of the triangle 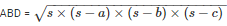
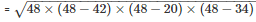
= 336cm2
Now, for the area of triangle BCD
Perimeter of triangle BCD 2s = BC + CD + BD
2s = 29cm + 21cm + 20cm
s = 35 cm
By using Heron’s Formula,
Area of the triangle BCD 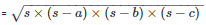
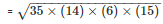
= 210cm2
Therefore, Area of quadrilateral ABCD = Area of triangle ABD + Area of triangle BCD
Area of quadrilateral ABCD = 336 + 210
Area of quadrilateral ABCD = 546 cm2
Q10. Find the perimeter and the area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, AC = 15 cm and angle ACB = 90∘.
Solution:
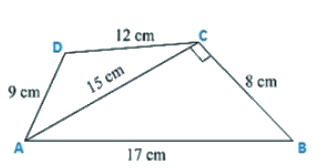
Given are the sides of the quadrilateral ABCD in which
AB = 17 cm, AD = 9 cm, CD = 12 cm, AC = 15 cm and an angle ACB = 90∘
By using Pythagoras theorem
BC2 = AB2−AC2
BC2 = 172−152
BC = 8 cm
Now, area of triangle 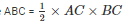
area of triangle 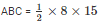
area of triangle ABC = 60 cm2
Now, for the area of triangle ACD
Perimeter of triangle ACD 2s = AC + CD + AD
2s = 15 + 12 +9
s = 18 cm
By using Heron’s Formula,
Area of the triangle ACD 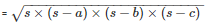
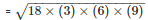
= 54cm2
Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ACD
Area of quadrilateral ABCD = 60 cm2 + 54cm2
Area of quadrilateral ABCD = 114 cm2
Q11. The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of parallelogram.
Solution:
Given,
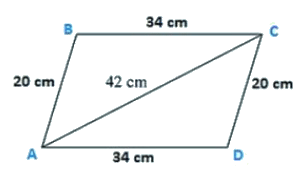
The adjacent sides of a parallelogram ABCD measures 34 cm and 20 cm, and the diagonal AC measures 42 cm.
Area of the parallelogram = Area of triangle ADC + Area of triangle ABC
Note: Diagonal of a parallelogram divides into two congruent triangles
Therefore,
Area of the parallelogram = 2 × (Area of triangle ABC)
Now, for area of triangle ABC
Perimeter = 2s = AB + BC + CA
2s = 34 cm + 20 cm + 42 cm
s = 48 cm
By using Heron’s Formula,
Area of the triangle ABC = 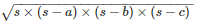
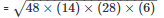
= 336cm2
Therefore, area of parallelogram ABCD = 2 × (Area of triangle ABC)
Area of parallelogram = 2 × 336cm2
Area of parallelogram ABCD = 672 cm2
Q12. Find the area of the blades of the magnetic compass shown in figure given below.
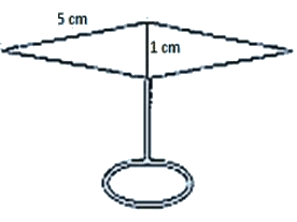
Solution:
Area of the blades of magnetic compass = Area of triangle ADB + Area of triangle CDB
Now, for the area of triangle ADB
Perimeter = 2s = AD + DB + BA
2s = 5 cm + 1 cm + 5 cm
s = 5.5 cm
By using Heron’s Formula,
Area of the triangle 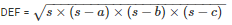
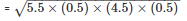
= 2.49cm2
Also, area of triangle ADB = Area of triangle CDB
Therefore area of the blades of the magnetic compass = 2 × area of triangle ADB
Area of the blades of the magnetic compass = 2 ×2.49
Area of the blades of the magnetic compass = 4.98 cm2
Q13. A hand fan is made by sticking 10 equal size triangular strips of two different types of paper as shown in the figure. The dimensions of equal strips are 25 cm, 25 cm and 14 cm. Find the area of each type of paper needed to make the hand fan.
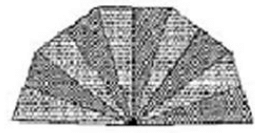
Solution:
Given that,
The sides of AOB
AO = 25 cm
OB = 25 cm
BA = 14 cm
Area of each strip = Area of triangle AOB
Now, for the area of triangle AOB
Perimeter = AO + OB + BA
2s = 25 cm +25 cm + 14 cm
s = 32 cm
By using Heron’s Formula,
Area of the triangle 
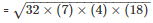
= 168cm2
Also, area of each type of paper needed to make a fan = 5 × Area of triangle AOB
Area of each type of paper needed to make a fan = 5 × 168 cm2
Area of each type of paper needed to make a fan = 840cm2
Q14. A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 13 cm, 14 cm and 15 cm and the parallelogram stands on the base 14 cm, find the height of a parallelogram.
Solution:
The sides of the triangle DCE are
DC = 15 cm,
CE = 13 cm,
ED = 14 cm
Let the h be the height of parallelogram ABCD
Now, for the area of triangle DCE
Perimeter = DC + CE + ED
2s = 15 cm + 13 cm + 14 cm
s = 21 cm
By using Heron’s Formula,
Area of the triangle 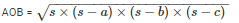
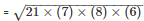
= 84cm2
Also, area of triangle DCE = Area of parallelogram ABCD ⇒ 84cm2
24 × h = 84cm2
h = 6 cm.
FAQs on RD Sharma Solutions Ex-12.2, (Part -2), Heron's Formula, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is Heron's formula? |  |
| 2. How is Heron's formula derived? |  |
| 3. Can Heron's formula be used for all types of triangles? |  |
| 4. Are there any limitations or conditions for using Heron's formula? |  |
| 5. How is Heron's formula different from other methods of finding the area of a triangle? |  |

|
Explore Courses for Class 9 exam
|

|

















