RD Sharma Solutions Ex-13.1, Linear Equation In Two Variables, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1: Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
(i) -2x + 3y = 12
(ii) x – y/2 – 5 = 0
(iii) 2x + 3y = 9.35
(iv) 3x = -7y
(v) 2x + 3 = 0
(vi) y – 5 = 0
(vii) 4 = 3x
(viii) y = x/2 ;
A 1 :
(i) We are given
– 2x + 3y = 12
– 2x + 3y – 12 = 0
Comparing the given equation with ax+ by+ c = O
We get, a = – 2; b = 3; c = -12
(ii) We are given
x – y/2 – 5= 0
Comparing the given equation with ax + by + c = 0 ,
We get, a = 1; b = -1/2, c = -5
(iii) We are given
2x + 3y = 9.35
2x + 3y – 9.35 =0
Comparing the given equation with ax + by + c = 0
We get, a = 2 ; b = 3 ; c = -9.35
(iv) We are given
3x = -7y
3x + 7y = 0
Comparing the given equation with ax+ by + c = 0,
We get, a = 3 ; b = 7 ; c = 0
(v) We are given
2x + 3 = 0
Comparing the given equation with ax + by + c = 0,
We get, a = 2 ; b = 0 ; c = 3
(vi) We are given
Y – 5 = 0
Comparing the given equation with ax + by+ c = 0,
We get, a = 0; b = 1; c = -5
(vii) We are given
4 = 3x
3x-4 = 0
Comparing the given equation with ax + by + c = 0,
We get, a = 3; b = 0; c = -4
(viii) We are given
Y = x/2
Taking L.C.M ⇒ x — 2y = 0
Comparing the given equation with ax + by + c = 0 ,
We get, a = 1; b = -2; c = 0
Q 2: Write each of the following as an equation in two variables:
(i) 2x = -3
(ii) y=3
(iii) 5x = 7/ 2
(iv) y = 3/2x
A 2:
(i) We are given,
2x = -3
Now, in two variable forms the given equation will be
2x + 0y + 3 = 0
(ii) We are given,
y = 3
Now, in two variable forms the given equation will be
0 x + y – 3 = 0
(iii) We are given,
5x = -7/2
Now, in two variable forms the given equation will be
5x + Oy +7/2 = 0
10x + Oy – 7 = 0
(iv) We are given,
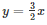 (Taking L.C.M on both sides)
(Taking L.C.M on both sides)
Now, in two variable forms the given equation will be
3x – 2y + 0 = 0
Q 3 : The cost of ball pen is Rs 5 less than half of the cost of fountain pen. Write this statement as a linear equation in two variables.
A 3:
Let the cost of fountain pen be y and cost of ball pen be x.
According to the given equation, we have
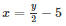
⇒ 2x = y – 10
⇒ 2x –y + 10 = 0
Here y is the cost of one fountain pen and x is that of one ball pen.
FAQs on RD Sharma Solutions Ex-13.1, Linear Equation In Two Variables, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is a linear equation in two variables? |  |
| 2. How can we solve a linear equation in two variables? |  |
| 3. Can a linear equation in two variables have more than one solution? |  |
| 4. How do we represent the solution of a linear equation in two variables graphically? |  |
| 5. Can a linear equation in two variables have different forms? |  |

|
Explore Courses for Class 9 exam
|

|

















