RD Sharma Solutions Ex-13.3, (Part -2), Linear Equation In Two Variables, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q8: From the choices given below, choose the equations whose graph is given in fig
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x
Ans: We are given co-ordinates (1, – 1) and (-1, 1) as the solution of one of the following equations.
We will substitute the value of both co-ordinates in each of the equation and find the equation which satisfies the given co-ordinates.
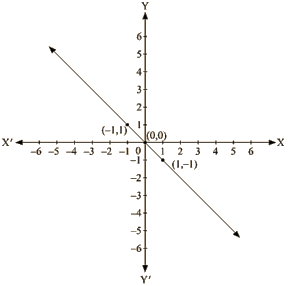
(i) We are given, y = x
Substituting x =I and y = -1 ,
we get; 1 ≠ -1
L.H.S ≠ R.H.S
Substituting x = -1 and y = 1 ,
we get; -1 ≠1
L.H.S ≠R.H.S
Therefore, the given equation y = x does not represent the graph in the figure.
(ii) We are given,
x + y = 0
Substituting x =1 and y = -1 , we get
⇒1 + (-1) = 0
⇒ 0 = 0
L.H.S = R.H.S
Substituting x = —1 and y = 1 ,we get
(-1)+ 1 = 0
0 = 0
L.H.S = R.H.S
Therefore, the given solutions satisfy this equation.
Thus, it is the equation whose graph is given.
Q9: From the choices given below, choose the equation whose graph is given fig:
(i) y = x + 2
(ii) y = x – 2
(iii)y = – x + 2
(iv) x + 2y = 6
Ans. We are given co-ordinates (-1, 3) and (2, 0) as the solution of one of the following equations.
We will substitute the value of both co-ordinates in each of the equation and find the equation which satisfies the given co-ordinates.
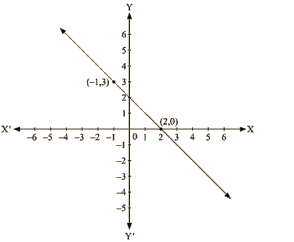
(i) We are given, y = x+2
Substituting x = – 1 and y = 3 ,we get
3 ≠ – 1 + 2
L.H.S ≠ R.H.S
Substituting x = 2 and y = 0 ,we get
0 ≠ 4
L.H.S ≠R.H.S
Therefore, the given solution does not satisfy this equation.
(ii) We are given, y = x – 2
Substituting x = —1 and y = 3 ,we get
3 = – 1 – 2
L.H.S ≠ R.H.S
Substituting x = 2 and y = 0 ,we get
0 = 0
L.H.S = R.H.S
Therefore, the given solutions does not completely satisfy this equation.
(iii) We are given, y = – x + 2
Substituting x = – 1 and y = 3,we get
3 = – (– 1) + 2
L.H.S = R.H.S
Substituting x = 2 and y = 0 ,we get
0 = -2 + 2
0 = 0
L.H.S = R.H.S
Therefore, the given solutions satisfy this equation.
Thus, it is the equation whose graph is given.
Q 10 : If the point (2, -2) lies on the graph of linear equation, 5x + 4y = 4, find the value of k.
Ans. It is given that the point (2,-2) lies on the given equation,
5x + ky = 4
Clearly, the given point is the solution of the given equation.
Now, Substituting x = 2 and y = – 2 in the given equation, we get 5x + ky = 4
5 x 2 + (– 2) k = 4
2k = 10 – 4
2k = 6
k = 6/2
k = 3
Q 11 : Draw the graph of equation 2x + 3y = 12. From the graph, find the co ordinates of the point:
(i) whose y-coordinate is 3
(ii) whose x coordinate is -3
Ans. We are given,
2x +3y =12
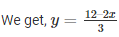
Substituting, x = 0 in 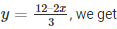
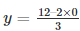
y = 4
Substituting x = 6 in 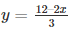
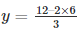
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 6 |
| Y | 4 | 0 |
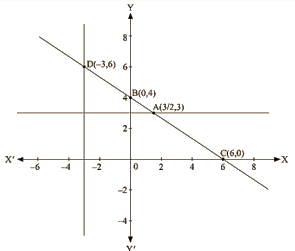
By plotting the given equation on the graph, we get the point B (0, 4) and C (6,0).
(i) Co-ordinates of the point whose y axis is 3 are A (3/2, 3)
(ii) Co-ordinates of the point whose x -coordinate is —3 are D (-3, 6)
Q 12: Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes:
(i) 6x – 3y = 12
(ii) – x + 4y = 8
(iii) 2x + y = 6
(iv) 3x + 2y + 6 = 0
Ans. (i) We are given,
6x – 3y = 12 We get,
y = (6x —12) /3
Now, substituting x = 0 in y = – (6x – 12)/3 we get
y =- 4
Substituting x = 2 in y = (- 6x —12)/3, we get
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| x | 0 | 2 |
| y | -4 | 0 |
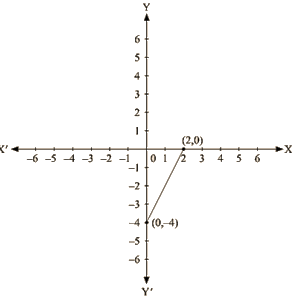
Co-ordinates of the points where graph cuts the co-ordinate axes are y = – 4 at y axis and x = 2 at x axis. (ii) We are given,
– x + 4y = 8
We get,
Now, substituting x = 0 in  we get
we get
y = 2
Substituting x = -8 in  we get
we get
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | -8 |
| Y | 2 | 0 |
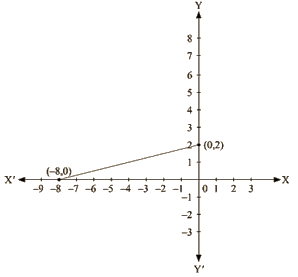
Co-ordinates of the points where graph cuts the co-ordinate axes are y = 2 at y axis and x = —8 at x axis.
(iii) We are given,
2x + y = 6
We get, y = 6 – 2x
Now, substituting x = 0 in y = 6 -2x we get
y = 6
Substituting x = 3 in y = 6-2x, we get
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 3 |
| Y | 6 | 0 |
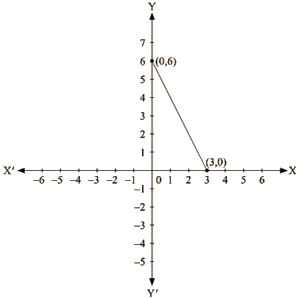
Co-ordinates of the points where graph cuts the co-ordinate axes are y = 6 at y axis and x =3 at x axis.
(iv) We are given,
3x+2y+6 = 0
We get,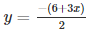
Now, substituting x = 0 in 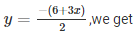
y= – 3
Substituting x = —2 in 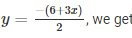
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | -2 |
| y | -3 | 0 |
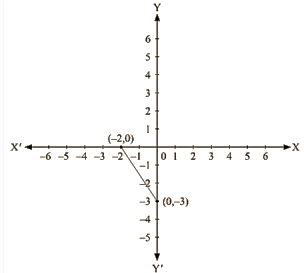
Co-ordinates of the points where graph cuts the co-ordinate axes are y = – 3 at y axis and x = – 2 at x axis.
Q 13 : Draw the graph of the equation 2x + y = 6. Shade the region bounded by the graph and the coordinate axes. Also, find the area of the shaded region.
Ans. We are given,
2x + y = 6
We get,
y = 6 – 2x
Now, substituting x = 0 in y = 6 – 2x,
we get y = 6
Substituting x =3 in y = 6— 2x,
we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 3 |
| Y | 6 | 0 |
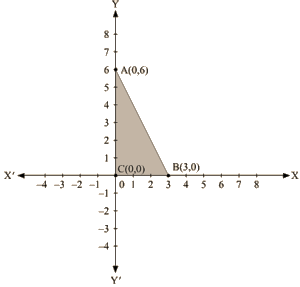
The region bounded by the graph is ABC which forms a triangle.
AC at y axis is the base of triangle having AC = 6 units on y axis.
BC at x axis is the height of triangle having BC = 3 units on x axis.
Therefore, Area of triangle ABC, say A is given by A = (Base x Height)/2
A = (AC x BC)/2
A = (6 x 3)/2
A = 9 sq. units
Q 14 : Draw the graph of the equation 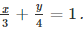 Also, find the area of the triangle formed by 3 4 the line and the coordinates axes.
Also, find the area of the triangle formed by 3 4 the line and the coordinates axes.
Ans. We are given.
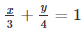
4x +3y = 12
We get,
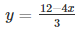
Now, substituting x = 0 in 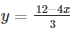 ,we get
,we get
y = 4
Substituting x = 3 in 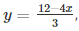 we get
we get
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 3 |
| Y | 4 | 0 |
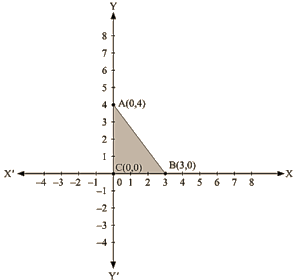
The region bounded by the graph is ABC which forms a triangle.
AC at y axis is the base of triangle having AC = 4 units on y axis.
BC at x axis is the height of triangle having BC = 3 units on x axis.
Therefore,
Area of triangle ABC, say A is given by
A = (Base x Height)/2
A= (AC x BC)/2
A = (4 x 3)/2
A = 6 sq. units
FAQs on RD Sharma Solutions Ex-13.3, (Part -2), Linear Equation In Two Variables, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of solving linear equations in two variables? |  |
| 2. How do we solve linear equations in two variables graphically? |  |
| 3. What are the different methods to solve linear equations in two variables algebraically? |  |
| 4. Can linear equations in two variables have more than one solution? |  |
| 5. How are linear equations in two variables used in real-life situations? |  |

|
Explore Courses for Class 9 exam
|

|

















