RD Sharma Solutions Ex-13.4, Linear Equation In Two Variables, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1: Give the geometric representations of the following equations
(a) on the number line
(b) on the Cartesian plane:
(i) x = 2
(ii) y + 3 = 0
(iii) y = 3
(iv) 2x + 9 = 0
(v) 3x – 5 = 0
Ans :
(i) We are given, x = 2
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
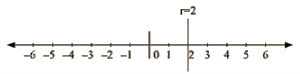
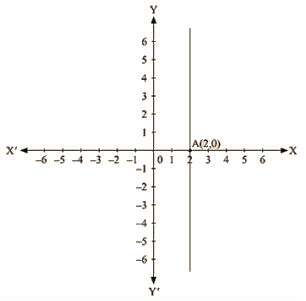
The representation of the solution on the Cartesian plane, it is a line parallel to y axis passing througl-the point (2, 0) is shown below
(ii) We are given, y + 3 = 0
We get, Y = -3
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
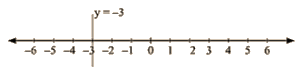
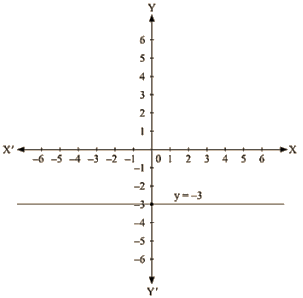
The representation of the solution on the Cartesian plane, it is a line parallel to x axis passing through the point A(0, —3) is shown below
(iii) we are given. y = 3
The representation of the solution on the number line. when given equation is treated as an equation in one variable.
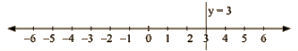
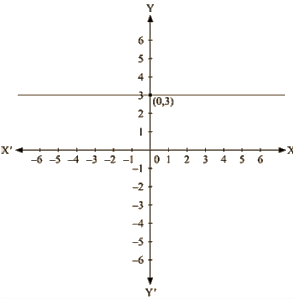
The representation of the solution on the Cartesian plane, it is a line parallel to x axis passing through the point (0, 3) is shown below
(iv) We are given, 2x +9 = 0
We get, 2x = -9 The representation of the solution on the number line, when given equation is treated as an equation in one variable.
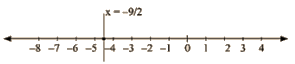
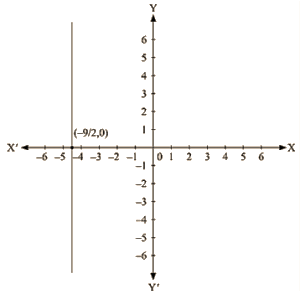
The representation of the solution on the Cartesian plane, it is a line parallel to y axis passing through the point ( -9/2,0) is shown below
(v) We are given, 3x —5 = 0
We get, 5 x = 3 The representation of the solution on the number line, when given equation is treated as an equation in one variable.
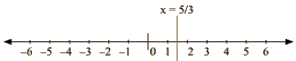
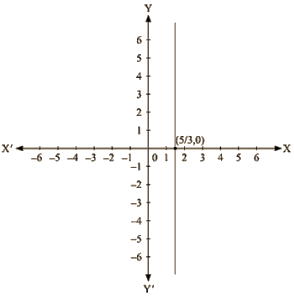
The representation of the solution on the Cartesian plane, it is a line parallel to y axis passing througl-the point (5,0) is shown below
Q 2 : Give the geometrical representation of 2x + 13 = 0 as an equation in
(i) one variable
(ii) two variables
Ans:
We are given,
2x +13 = 0
We get,
2x = -13
x = -13/2
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
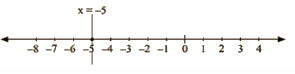
The representation of the solution on the Cartesian plane, it is a line parallel to y axis passing through the point (-13/2 , 0) is shown below.
Q3:. Solve the equation 3x + 2 = x – 8, and represent the solution on
(i) the number line
(ii) the Cartesian plane.
Ans : We are given,
3x + 2 = x – 8
we get,
3x – x = -8 – 2
2x = -10
x = -5
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
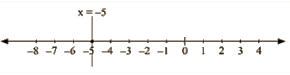
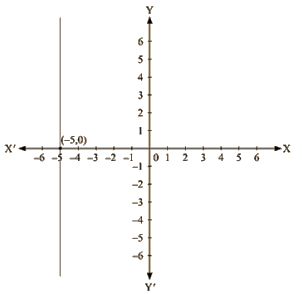
The representation Of the solution on the Cartesian plane, it is a line parallel to y axis passing through the point (-5, 0) is shown below
Q 4: Write the equation of the line that is parallel to x-axis and passing through the points
(i) (0,3)
(ii) (0, – 4)
(iii) (2,-5)
(iv) (3,4)
Ans:
(i) We are given the co-ordinates of the Cartesian plane at (0,3).
For the equation of the line parallel to x axis, we assume the equation as a one variable equation independent of x containing y equal to 3.
We get the equation as y = 3
(ii) We are given the co-ordinates of the Cartesian plane at (0,-4).
For the equation of the line parallel to x axis, we assume the equation as a one variable equation Independent of x containing y equal to -4.
We get the equation as y = -4
(iii) We are given the co-ordinates of the Cartesian plane at (2,-5).
For the equation of the line parallel to x axis, we assume the equation as a one variable equation independent of x containing y equal to -5.
We get the equation as y = -5
(iv) We are given the co-ordinates of the Cartesian plane at (3,4).
For the equation of the line parallel to x axis, we assume the equation as a one variable equation independent of x containing y equal to 4.
We get the equation as
y = 4
Q 5 : Write the equation of the line that is parallel to y-axis and passing through the Points
(i) (4,0)
(ii) (-2,0)
(iii) (3,5)
(iv) (- 4, – 3)
Ans:
(i) We are given the coordinates of the Cartesian plane at (4,0)-
For the equation of the line parallel to y axis ,we assume the equation as a one variable equation independent of y containing x equal to 4
We get the equation as y = 3
(ii) We are given the coordinates of the Cartesian plane at (-2,0) –
For the equation of the line parallel to y axis, we assume the equation as a one variable equation independent of y containing x equal to -2
We get the equation as y = -4
(iii) We are given the coordinates of the Cartesian plane at (3,5)-
For the equation of the line parallel to y axis, we assume the equation as a one variable equation independent of y containing x equal to 3
We get the equation as y = -5
(iv) We are given the coordinates of the Cartesian plane at (-4,-3)-
For the equation of the line parallel to y axis, we assume the equation as a one variable equation independent of y containing x equal to -4
We get the equation as y = 4
FAQs on RD Sharma Solutions Ex-13.4, Linear Equation In Two Variables, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are linear equations in two variables? |  |
| 2. How do you solve linear equations in two variables? |  |
| 3. How can linear equations in two variables be represented graphically? |  |
| 4. What is the importance of linear equations in two variables in real-life applications? |  |
| 5. Can linear equations in two variables have infinitely many solutions? |  |

|
Explore Courses for Class 9 exam
|

|

















