RD Sharma Solutions Ex-14.1, Quadrilaterals, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
1) Three angles of a quadrilateral are respectively equal to 1100, 500 and 400. Find its fourth angle.
Solution:
Given,
Three angles are 1100, 500 and 400
Let the fourth angle be ‘x’
We have,
Sum of all angles of a quadrilateral = 3600
1100 + 500 + 400 = 3600
⇒ x = 3600 – 2000
⇒x = 1600
Therefore, the required fourth angle is 1600.
2) In a quadrilateral ABCD, the angles A, B, C and D are in the ratio of 1:2:4:5. Find the measure of each angles of the quadrilateral.
Solution:
Let the angles of the quadrilaterals be
A = x, B = 2x, C = 4x and D = 5x
Then,
A + B + C + D = 3600
⇒ x + 2x + 4x + 5x = 3600
⇒ 12x = 3600
⇒ 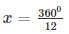
⇒ x = 300
Therefore, A = x = 300
B = 2x = 600
C = 4x = 1200
D = 5x = 1500
3) In a quadrilateral ABCD, CO and Do are the bisectors of ∠Cand∠D respectively. Prove that ∠COD = 1/2(∠Aand∠B).
Solution:
InΔDOC
∠1+∠COD+∠2=1800 [Angle sum property of a triangle]
⇒ ∠COD = 180−(∠1−∠2)
⇒ ∠COD = 180−∠1+∠2
⇒ 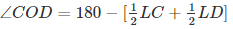 [∵ OC and Od are bisectors of LC and LD respectively]
[∵ OC and Od are bisectors of LC and LD respectively]
⇒ 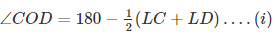
In quadrilateral ABCD
∠A+∠B+∠C+∠D = 3600 [Angle sum propert yof quadrilateral]
∠C+∠D=3600−(∠A+∠B)….(ii)
Substituting (ii) in (i)
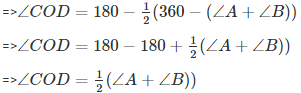
4) The angles of a quadrilateral are in the ratio 3:5:9:13. Find all the angles of the quadrilateral.
Solution:
Let the common ratio between the angles is ‘t’
So the angles will be 3t, 5t, 9t and 13t respectively.
Since the sum of all interior angles of a quadrilateral is 3600
Therefore, 3t + 5t + 9t + 13t = 3600
⇒ 30t = 3600
⇒ t = 120
Hence, the angles are
3t = 3*12 = 360
5t = 5*12 = 600
9t = 9*12 = 1080
13t = 13*12 = 1560
FAQs on RD Sharma Solutions Ex-14.1, Quadrilaterals, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are the properties of a quadrilateral? |  |
| 2. How many types of quadrilaterals are there? |  |
| 3. What is the sum of interior angles of a quadrilateral? |  |
| 4. How do you prove that a quadrilateral is a parallelogram? |  |
| 5. What is the difference between a rectangle and a square? |  |

|
Explore Courses for Class 9 exam
|

|

















