RD Sharma Solutions Ex-14.3, Quadrilaterals, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q.1. In a parallelogram ABCD, determine the sum of angles ∠C and ∠D.
Solution:
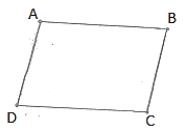
∠C and ∠D are consecutive interior angles on the same side of the transversal CD.
∴∠C+∠D = 1800
Q.2. In a parallelogram ABCD, if ∠B = 1350, determine the measures of its other angles.
Solution:
Given ∠B = 1350
ABCD is a parallelogram
∴∠A = ∠C,∠B =∠Dand∠A+∠B = 1800
⇒∠A+1350 = 1800
⇒∠A = 450
⇒∠A = ∠C = 450 and ∠B = ∠C = 1350
Q.3. ABCD is a square. AC and BD intersect at O. State the measure of ∠AOB.
Solution:
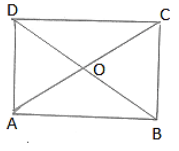
Since, diagonals of a square bisect each other at right angle.
∴ ∠AOB = 900
Q.4. ABCD is a rectangle with ∠ABD = 400. Determine ∠DBC
Solution:
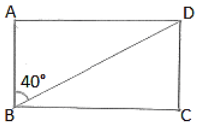
We have,
∠ABC = 900
⇒∠ABD+∠DBC = 900 [∵∠ABD = 400]
⇒400+∠DBC = 900
∴∠DBC = 500
Q.5. The sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
Solution:
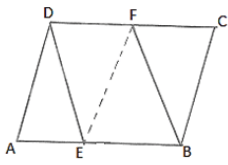
Since ABCD is a parallelogram
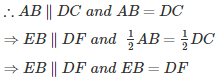
EBFD is a parallelogram.
Q.6. P and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
Solution:
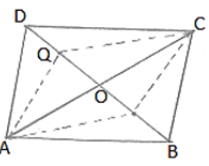
We know that,
Diagonals of a parallelogram bisect each other.
Therefore, OA = OC and OB = OD
Since P and Q are point of intersection of BD.
Therefore, BP = PQ = QD
Now, OB = OD are BP = QD
⇒ OB – BP = OD – QD
⇒ OP = OQ
Thus in quadrilateral APCQ, we have
OA = OC and OP = OQ
Diagonals of Quadrilateral APCQ bisect each other.
Therefore APCQ is a parallelogram.
Hence AP∥CQ.
Q.7. ABCD is a square. E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
Solution:
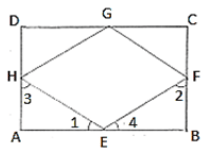
We have,
AE = BF = CG = DH = x (say)
BE = CF = DG = AH = y (say)
In ΔAEH and ΔBEF,we have
AE = BF
∠A=∠B
And AH = BE
So, by SAS congruency criterion, we have
ΔAEH≃ΔBFE
⇒∠1 = ∠2 and ∠3 = ∠4
But ∠1+∠3 = 900 and ∠2+∠A = 900
⇒ ∠1+∠3+∠2+∠A = 900+900
⇒ ∠1+∠4+∠1+∠4 = 1800
⇒ 2(∠1+∠4) = 1800
⇒ ∠1+∠4 = 900
HEF = 900
Similarly we have ∠F = ∠G = ∠H = 900
Hence, EFGH is a Square.
Q.8. ABCD is a rhombus, EAFB is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles.
Solution:
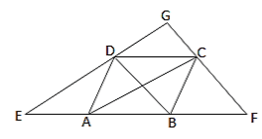
We know that the diagonals of a rhombus are perpendicular bisector of each other.
∴OA = OC,OB = OD,and∠AOD = ∠COD = 900
And ∠AOB = ∠COB = 900
In ΔBDE, A and O are mid-points of BE and BD respectively.
OA∥DE
OC∥DG
In ΔCFA, B and O are mid-points of AF and AC respectively.
OB∥CF
OD∥GC
Thus, in quadrilateral DOGC, we have
OC∥DGandOD∥GC
⇒ DOCG is a parallelogram
∠DGC = ∠DOC
∠DGC = 900
Q.9. ABCD is a parallelogram, AD is produced to E so that DE = DC and EC produced meets AB produced in F. Prove that BF = BC.
Solution:
Draw a parallelogram ABCD with AC and BD intersecting at O.
Produce AD to E such that DE = DC
Join EC and produce it to meet AB produced at F.

In ΔDCE,
∠DCE =∠DEC…..(i) [In a triangle, equal sides have equal angles]
AB∥CD [Opposite sides of the parallelogram are parallel]
∴AE∥CD [AB lies on AF]
AF∥CD and EF is the Transversal.
∠DCE = ∠BFC…..(ii) [Pair of corresponding angles]
From (i) and (ii) we get
∠DEC = ∠BFC
In ΔAFE,
∠AFE = ∠AEF [∠ DEC = ∠ BFC]
Therefore, AE = AF [In a triangle, equal angles have equal sides opposite to them]
⇒ AD + DE = AB + BF
⇒BC + AB = AB + BF [Since, AD = BC, DE = CD and CD = AB, AB = DE]
⇒ BC = BF
Hence proved.
FAQs on RD Sharma Solutions Ex-14.3, Quadrilaterals, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are the different types of quadrilaterals? |  |
| 2. How can I identify if a given quadrilateral is a square? |  |
| 3. What are the properties of a parallelogram? |  |
| 4. How can I find the area of a trapezium? |  |
| 5. What is the difference between a rhombus and a square? |  |

|
Explore Courses for Class 9 exam
|

|

















