RD Sharma Solutions Ex-14.4, (Part - 1), Quadrilaterals, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q.1. In ΔABC, D, E and F are, respectively the mid points of BC, CA and AB. If the lengths of sides AB, BC and CA are 7cm, 8cm and 9cm, respectively, find the perimeter of ΔDEF.
Solution:
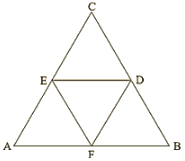
Given that,
AB = 7cm, BC = 8cm, AC = 9cm
In ∆ABC,
F and E are the mid points of AB and AC.
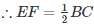
Similarly

Perimeter of ∆DEF = DE + EF + DF

=12cm
∴ Perimeterof ΔDEF = 12cm
Q.2. In a ΔABC, ∠A=500, ∠B=600 and ∠C=700. Find the measures of the angles of the triangle formed by joining the mid-points of the sides of this triangle.
Solution:
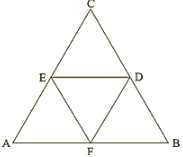
In ΔABC,
D and E are mid points of AB and BC.
By Mid point theorem,
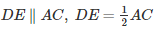
F is the midpoint of AC
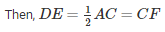
In a Quadrilateral DECF
DE∥AC,DE = CF
Hence DECF is a parallelogram.
∴∠C =∠D = 700 [Opposite sides of a parallelogram]
Similarly
BEFD is a parallelogram, ∠B =∠F = 600
ADEF is a parallelogram, ∠A = ∠E = 500
∴ Angles of ΔDEF are
∠D = 700,∠E = 500,∠F = 600
Q.3. In a triangle, P, Q and R are the mid points of sides BC, CA and AB respectively. If AC = 21cm, BC = 29cm and AB = 30cm, find the perimeter of the quadrilateral ARPQ.
Solution:
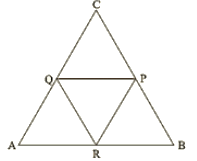
In ΔABC,
R and P are mid points of AB and BC
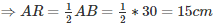 [By Mid point Theorem]
[By Mid point Theorem]
In a quadrilateral,
[A pair of side is parallel and equal]
RP∥AQ,RP = AQ
Therefore, RPQA is a parallelogram
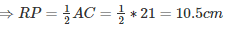
AR = QP = 15cm [Opposite sides are equal]
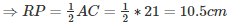
RP = AQ = 10.5cm [Opposite sides are equal ]
Now,
Perimeter of ARPQ = AR + QP + RP +AQ
= 15 +15 +10.5 +10.5
= 51cm
Q.4. In a ΔABC median AD is produced to X such that AD = DX. Prove that ABXC is a parallelogram.
Solution:
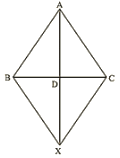
In a quadrilateral ABXC, we have
AD = DX [Given]
BD = DC [Given]
So, diagonals AX and BC bisect each other.
Therefore, ABXC is a parallelogram.
Q.5. In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC intersects FE at Q. Prove that AQ = QP.
Solution:
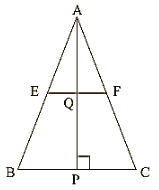
In a ΔABC
E and F are mid points of AB and AC
 [By mid point theorem]
[By mid point theorem]
In ΔABP
F is the mid-point of AB and ∴ FQ∥BP[∵EF∥BP]
Therefore, Q is the mid-point of AP [By mid-point theorem]
Hence, AQ = QP.
Q6. In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing through A. If L is the mid-point of BC, prove that ML = NL.
Solution:
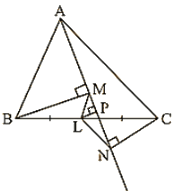
Given that,
In ΔBLMandΔCLN
∠BML=∠CNL= 900
BL = CL [L is the mid-point of BC]
∠MLB = ∠NLC [Vertically opposite angle]
∴ΔBLM = ΔCLN
∴LM = LN [corresponding parts of congruent triangles]
Q.7. In figure 14.95, Triangle ABC is a right angled triangle at B. Given that AB = 9cm, AC = 15cm and D, E are the mid-points of the sides AB and AC respectively, calculate
(i) The length of BC
(ii) TheareaofΔADE.
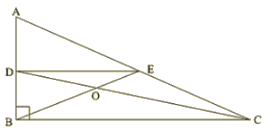
Solution:
In ΔABC,∠B= 900,
By using Pythagoras theorem
AC2 = AB2 + BC2
⇒152 = 92 + BC2
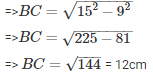
D and E are mid-points of AB and AC
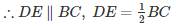 [By mid−point theorem]
[By mid−point theorem]
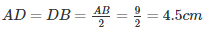 [∵D is the mid−point of AB]]
[∵D is the mid−point of AB]]
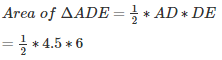
=13.5cm2
Q.8. In figure 14.96, M, N and P are mid-points of AB, AC and BC respectively. If MN = 3cm, NP = 3.5cm and MP = 2.5cm, calculate BC, AB and AC.
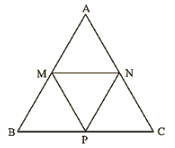
Solution:
Given MN = 3cm, NP = 3.5cm and MP = 2.5cm.
To find BC, AB and AC
In ΔABC
M and N are mid-points of AB and AC
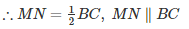 [By mid−point theorem]
[By mid−point theorem]
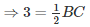
⇒ 3∗2 = BC
⇒ BC = 6cm
Similarly
AC = 2MP = 2 (2.5) = 5cm
AB = 2 NP = 2 (3.5) = 7cm
Q.9. ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R. Prove that the perimeter of ΔPQR is double the perimeter of ΔABC.
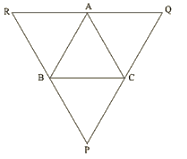
Solution:
Clearly ABCQ and ARBC are parallelograms.
Therefore, BC = AQ and BC = AR
⇒AQ = AR
⇒A is the mid-point of QR
Similarly B and C are the mid points of PR and PQ respectively.
⇒ PQ = 2AB, QR = 2BC and PR = 2CA
⇒ PQ + QR + RP = 2 (AB + BC + CA)
⇒ Perimeter of ΔPQR = 2 (perimeter of ΔABC)
Q.10. In figure 14.97, BE⊥AC, AD is any line from A to BC intersecting BE in H. P, Q and R are respectively the mid-points of AH, AB and BC. Prove that ∠PQR=900
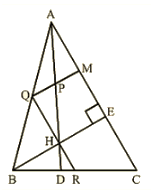
Solution:
Given,
BE⊥AC and P, Q and R are respectively mid-point of AH, AB and BC.
To prove: ∠PQR = 900
Proof: In ΔABC, Q and R are mid-points of AB and BC respectively.
∴ QR∥AC…..(i)
In ΔABH, Q and P are the mid-points of AB and AH respectively
∴ QP∥BH….(ii)
But, BE⊥AC
Therefore, from equation (i) and equation (ii) we have,
QP⊥QR
⇒∠PQR = 900
Hence Proved
FAQs on RD Sharma Solutions Ex-14.4, (Part - 1), Quadrilaterals, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are the properties of a quadrilateral? |  |
| 2. How many types of quadrilaterals are there? |  |
| 3. How can we prove that a quadrilateral is a parallelogram? |  |
| 4. How do we find the area of a quadrilateral? |  |
| 5. How do we find the perimeter of a quadrilateral? |  |
















