RD Sharma Solutions Ex-2.1, Exponents Of Real Numbers, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q.1. Simplify the following:
(i) 3(a4 b3)10 x 5 (a2 b2)3
Solution: = 3(a40 b30) x 5 (a6 b6) = 15 (a46 b36)
(ii) (2x -2 y3)3
Solution: = (23 x -2x3 y3x3) = 8x -6 y9
(iii) 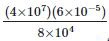
Solution: 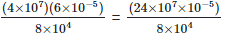
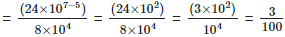
(iv) 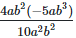
Solution: = 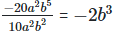
(v) 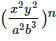
Solution: 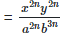
(vi) 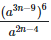
Solution: 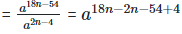 = a16n−50
= a16n−50
2. If a = 3 and b = -2, find the values of:
(i) aa+bb
(ii) ab+ba
(iii) ab+ba
Solution: (i) We have,aa+bb = 33+(−2)−2 = 33+ 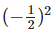 = 27+1/4 = 109/4
= 27+1/4 = 109/4
(ii) ab+ba = 3−2+(−2)3 = (1/3)2+(−2)3 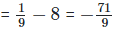
(iii) We have, ab+ba = (3+(−2))3(−2) = (3−2))−6 = 1−6 = 1
3.Prove that: (i) 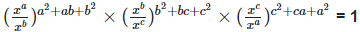
(ii) 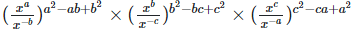
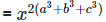
(iii) 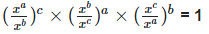
Solution: 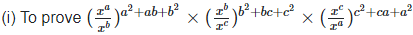 = 1
= 1
Left hand side (LHS) = Right hand side (RHS) Considering LHS,
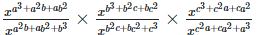
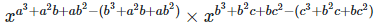
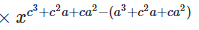
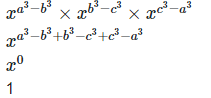
Or, Therefore, LHS = RHS Hence proved
(ii) To prove, 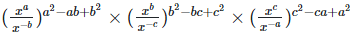
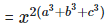
Left hand side (LHS) = Right hand side (RHS) Considering LHS,
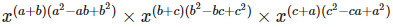
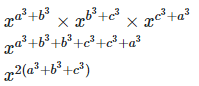
Therefore, LHS = RHS Hence proved (iii) To prove, 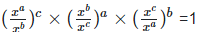
Left hand side (LHS) = Right hand side (RHS) Considering LHS,
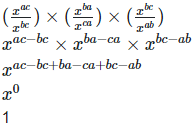
Therefore, LHS = RHS Hence proved
4. Prove that: (i) 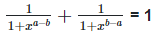
(ii) 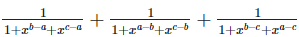
Solution: (i) 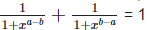
Left hand side (LHS) = Right hand side (RHS) Considering LHS,
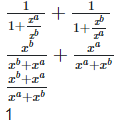
Therefore, LHS = RHS Hence proved
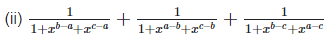
Left hand side (LHS) = Right hand side (RHS) Considering LHS,
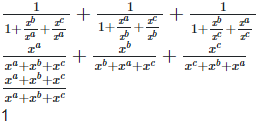
Therefore, LHS = RHS Hence proved
5.Prove that: (i) 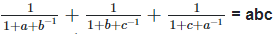
(ii) 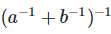
Solution: (i) To prove, 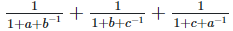 = abc
= abc
Left hand side (LHS) = Right hand side (RHS) Considering LHS,
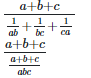
abc
Therefore, LHS = RHS Hence proved (ii) To prove, 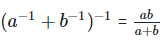
Left hand side (LHS) = Right hand side (RHS) Considering LHS,
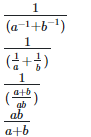
Therefore, LHS = RHS Hence proved
6. If abc = 1, show that 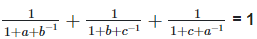
Solution: To prove, 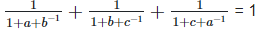
Left hand side (LHS) = Right hand side (RHS) Considering LHS,
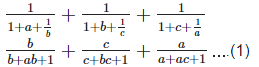
We know abc = 1
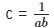
By substituting the value c in equation (1), we get
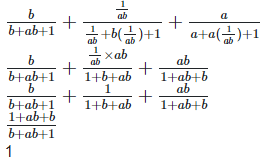
Therefore, LHS = RHS Hence proved
7. Simplify: (i) 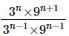
Solution: 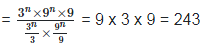
(ii) 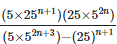
Solution: = 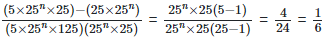
(iii) 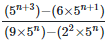
Solution: = 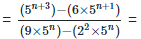
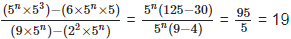
(iv) 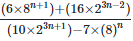
Solution: 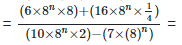
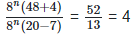
8. Solve the following equations for x:
(i) 72x+3 = 1
(ii) 2x+1=4x−3
(iii) 25x+3 = 8x+3
(iv) 42x = 13/2
(v) 4x−1×(0.5)3−2x=(1/8)x
(vi) 23x−7 = 256
Solution: (i) We have,
⇒ 72x+3 = 1 ⇒ 72x+3 = 70 ⇒ 2x + 3 = 0 ⇒ 2x = -3 ⇒ x 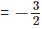
(ii) We have,
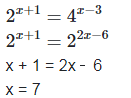
(iii) We have,
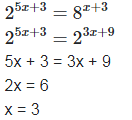
(iv) We have,
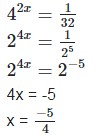
(v) We have,
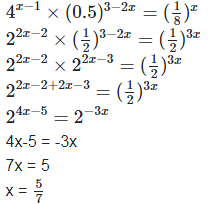
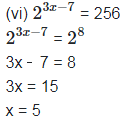
9. Solve the following equations for x:
(i) 22x−2x+3+24 = 0
(ii) 32x+4+1=2×3x+2
Solution:
(i) We have, ⇒ 22x−2x+3+24 = 0
⇒ 22x+24=2x.23
⇒ Let 2x=y
⇒ y2+24=y×23
⇒ y2−8y+16=0
⇒ y2−4y−4y+16=0
⇒ y(y-4) -4(y-4) = 0
⇒ y = 4
⇒ x2=22
⇒ x = 2
(ii) We have,
32x+4+1=2×3x+2
(3x+2)2+1=2×3x+2
Let 3x+2 = y
y2+1=2y
y2−2y+1=0
y2−y−y+1=0
y(y−1)−1(y−1)=0
(y−1)(y−1)=0
y = 1
10. If 49392 = a4b2c3, find the values of a, b and c, where a, b and c, where a, b, and c are different positive primes.
Solution: Taking out the LCM , the factors are 24,32 and 73 a4b2c3 = 24,32 and 73
a = 2, b = 3 and c = 7 [Since, a, b and c are primes]
11. If 1176 = 2a×3b×7c, Find a, b, and c.
Solution: Given that 2, 3 and 7 are factors of 1176. Taking out the LCM of 1176, we get 23×31×72 = 2a×3b×7c By comparing, we get
a = 3, b = 1 and c = 2.
12. Given 4725 = 3a×5b×7c, find (i) The integral values of a, b and c
Solution: Taking out the LCM of 4725, we get
33×52×71 = 3a×5b×7c
By comparing, we get
a = 3, b = 2 and c = 1.
(ii) The value of 2−a×3b×7c
Solution:
= 2−3×32×71
2−3×32×71 = 1/8×9×7
63/8
13. If a = xyp−1, b = xyq−1 and c = xyr−1, prove that aq−rbr−pcp−q = 1
Solution: Given, a = xyp−1, b = xyq−1 and c = xyr−1
To prove, aq−rbr−pcp−q = 1
Left hand side (LHS) = Right hand side (RHS) Considering LHS, = aq−rbr−pcp−q ……(i)
By substituting the value of a, b and c in equation
(i), we get
= (xyp−1)q−r(xyq−1)r−p(xyr−1)p−q
= xypq−pr−q+rxyqr−pq−r+pxyrp−rq−p+q
= xypq−pr−q+r+qr−pq−r+p+rp−rq−p+q
= xy0 = 1
FAQs on RD Sharma Solutions Ex-2.1, Exponents Of Real Numbers, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are exponents of real numbers? |  |
| 2. How do exponents of real numbers work? |  |
| 3. Can exponents of real numbers be negative? |  |
| 4. How are exponents of real numbers used in real-life situations? |  |
| 5. Can exponents of real numbers be fractional or decimal? |  |





















