RD Sharma Solutions Ex-2.2, (Part - 1), Exponents Of Real Numbers, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
1. Assuming that x,y,z are positive real numbers, simplify each of the following
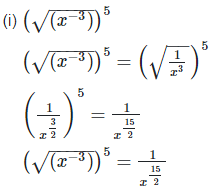
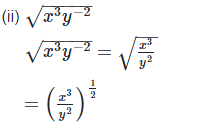

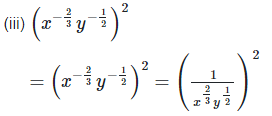
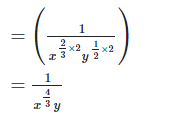
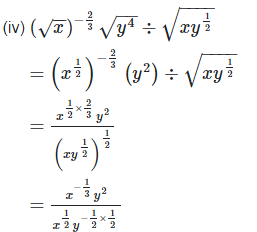
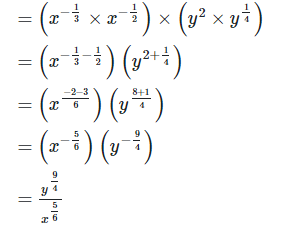
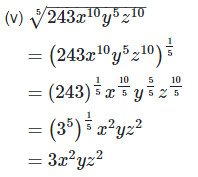
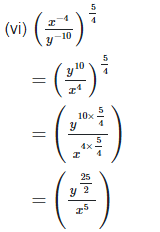
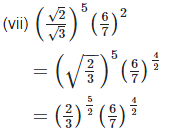
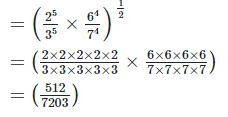
2. Simplify
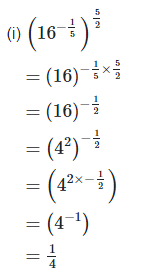
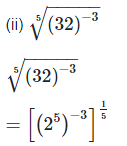
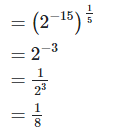
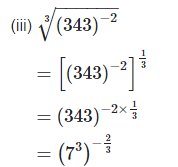
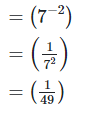
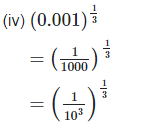
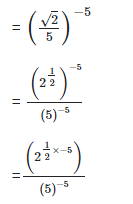
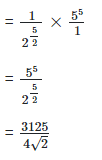
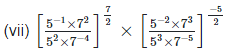
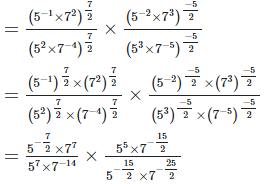
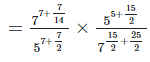

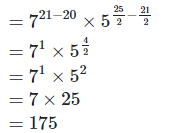
3. Prove that
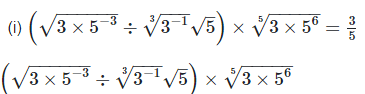
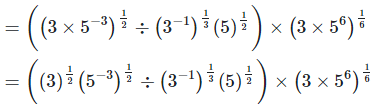
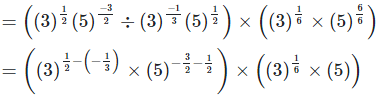
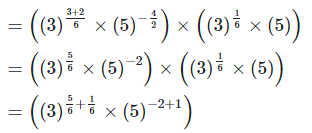
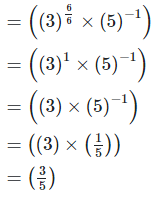
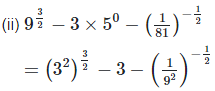

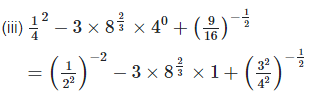
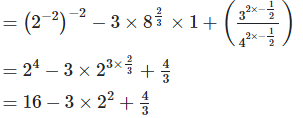
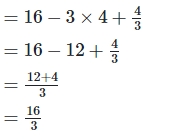
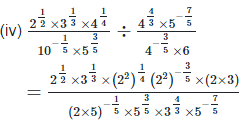

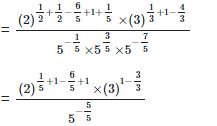
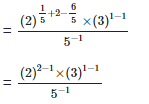
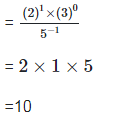
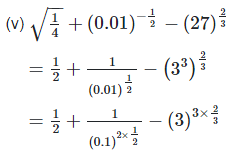
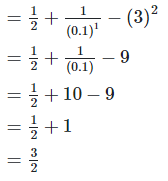
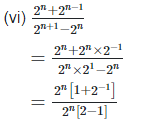
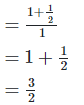
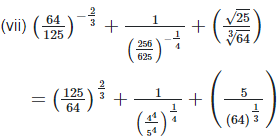
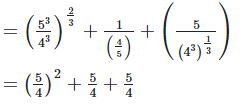
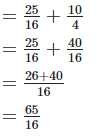
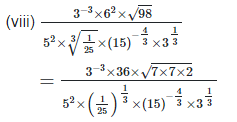
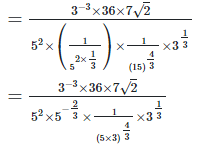
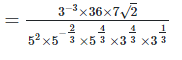
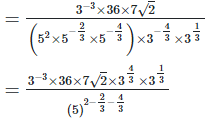
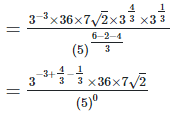
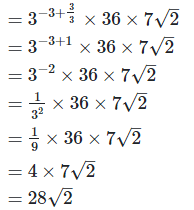
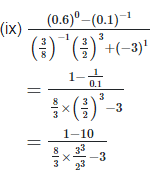
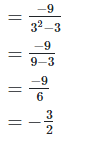
4. Show that
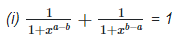
Left hand side (LHS) = Right hand side (RHS)
Considering LHS,
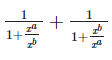

Therefore, LHS = RHS
Hence proved
(ii) 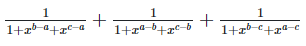
Left hand side (LHS) = Right hand side (RHS)
Considering LHS,
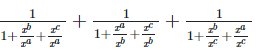
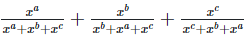
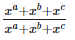
1
Therefore, LHS = RHS
Hence proved
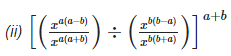
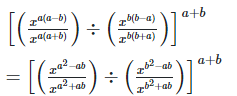
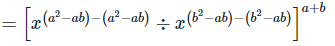
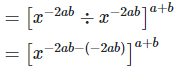
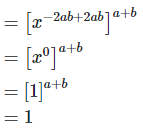
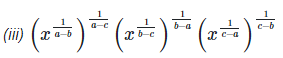
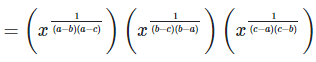
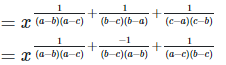
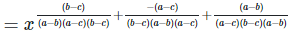
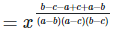
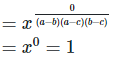
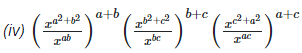
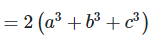
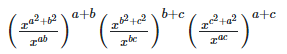
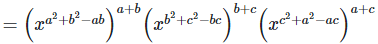
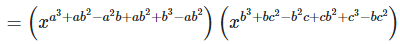
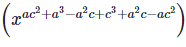
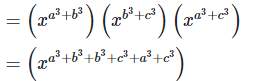
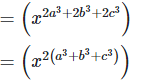
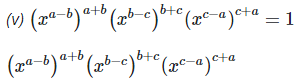
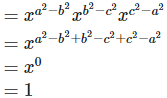
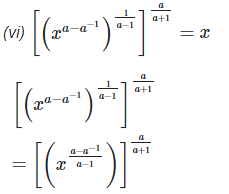
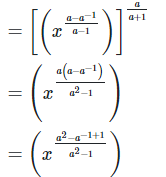
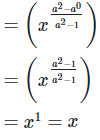
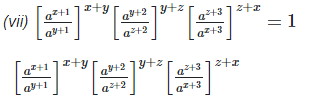
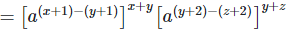
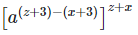
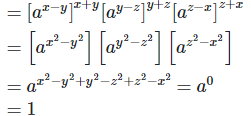
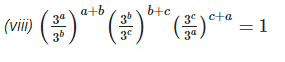
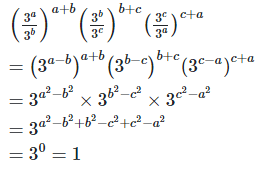
5. If 2x = 3y = 12z , 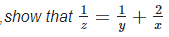
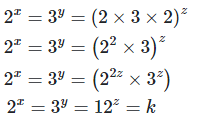
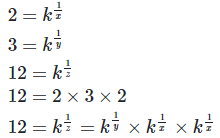
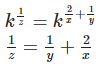
6. If 2x = 3y = 6−z , 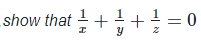
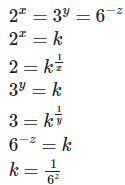
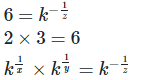
 [by equating exponents]
[by equating exponents]
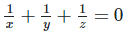
7. If ax = by = cz and b2 = ac , then show that 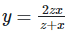
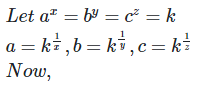
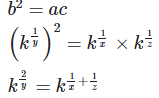
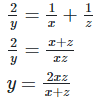
8. If 3x = 5y = (75)z, show that
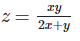
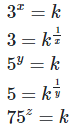
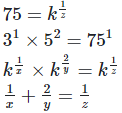
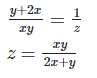
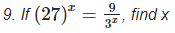
We have,
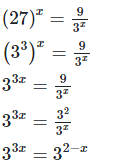
3x = 2 − x [On equating exponents]
3x + x = 2
4x = 2
x = 2/4
x = 12
Here the value of x is 1/2
10. Find the values of x in each of the following
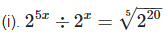
We have
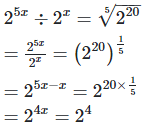
= 4x = 4 [On equatinge xponent]
x = 1
Hence the value of x is 1
(ii). (23)4 = (22)x
We have
(23)4 = (22)x
= 23×4 = 22×x
12 = 2x
2x = 12 [On equating exponents]
x = 6
Hence the value of x is 6
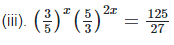
We have
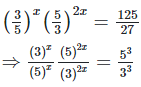
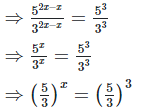
x = 3 [on equating exponents]
Hence the value of x is 3
(iv) 5x−2×32x−3 = 135
We have,
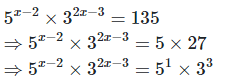
⇒ x − 2 = 1,2x − 3 = 3 [On equating exponents]
⇒ x = 2 + 1,2x = 3 + 3
⇒ x = 3, 2x = 6 ⇒ x = 3
Hence the value of x is 3
(v). 2x−7×5x−4 = 1250
We have
2x−7×5x−4 = 1250
⇒ 2x−7×5x−4 = 2×625
⇒ 2x−7×5x−4 = 2×54
⇒ x−7 = 1 ⇒ x = 8,x−4 = 4 ⇒ x = 8
Hence the value of x is 8
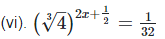
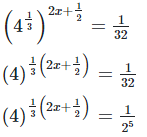
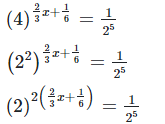
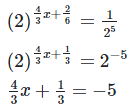
4x+1 = −15
4x = −15−1
4x = −16
x =−16/4
x = −4
Hence the value of x is 4
(vii). 52x+3 = 1
52x+3 = 1×50
2x+3 = 0 [By equatinge xponents]
2x = −3
x = −3/2
Hence the value of x is −3/2
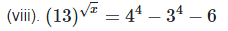
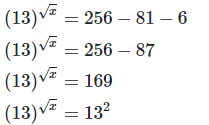
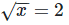 [By equating exponents]
[By equating exponents]
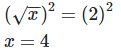
Hence the value of x is 4
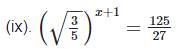
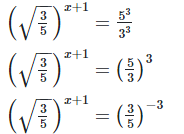
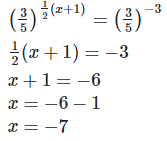
Hence the value of x is 7
FAQs on RD Sharma Solutions Ex-2.2, (Part - 1), Exponents Of Real Numbers, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are exponents of real numbers? |  |
| 2. How do you simplify expressions with exponents? |  |
| 3. What is the difference between a positive exponent and a negative exponent? |  |
| 4. How do you simplify expressions with negative exponents? |  |
| 5. Can exponents of real numbers be fractions or decimals? |  |

















