Class 9 Exam > Class 9 Notes > RD Sharma Solutions for Class 9 Mathematics > RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths
RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
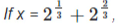show that x3 − 6x = 6
x3 − 6x = 6
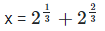
Putting cube on both the sides, we get
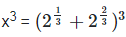
As we know, (a+b)3 = a3 + b3 + 3ab(a+b)
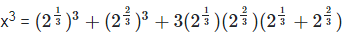
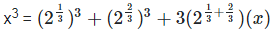
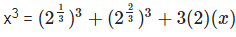
x3 = 6 + 6x
x3 – 6x = 6
Hence proved
12. Determine (8x)x, if 9x+2 = 240 + 9x.
9x+2 = 240 + 9x
9x .92 = 240 + 9x
Let 9x be y
81y = 240 + y
81y – y = 240
80y = 240
y = 3
Since, y = 3
Then,
9x = 3
32x = 3
Therefore, x = 1/2
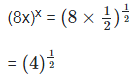
= 2
Therefore (8x)x = 2
13. If 3x+1 = 9x-2, find the value of 21+x
3x+1 = 9x-2
3x+1 = 32x-4
x + 1 = 2x – 4
x = 5
Therefore the value of 21+x = 21+5 = 26 = 64
14. If 34x = (81)-1 and (10)1/y = 0.0001, find the value of 2-x+4y.
34x = (81)-1 and (10)1/y = 0.0001
34x = (3)-4
x = -1
And (10)1/y = 0.0001
(10)1/y = (10)−4
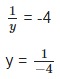
To find the value of 2-x+4y, we need to substitute the value of x and y
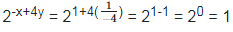
15. If 53x = 125 and 10y = 0.001. Find x and y.
53x = 125 and 10y = 0.001
53x = 53
x = 1
Now,
10y = 0.001
10y = 10-3
y = -3
Therefore, the value of x = 1 and the value of y = -3
16. Solve the following equations
(i) 3x+1 = 27×34
3x+1 = 33×34
3x+1 = 33+4
x + 1 = 3 + 4 [By equating exponents]
x + 1 = 7
x = 7 − 1
x = 6
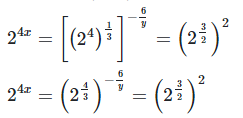
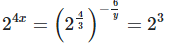
24x = 23
4x = 3 (By equating exponents)
x = 3/4
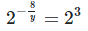
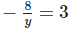(By equating exponents)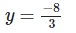
(iii). 3x−1×52y−3 = 225
3x−1×52y−3 = 32×52
x−1 = 2 [By equating exponents]
x = 3
3x−1×52y−3 = 32×52
2y−3 = 2 [By equating exponents]
2y = 5
y = 5/2
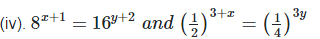
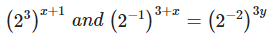
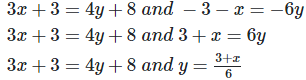
3x+3 = 4y+8 —eq1
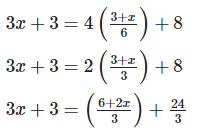
3(3x+3) = 6+2x+24
9x+9 = 30+2x
7x = 21
x = 21/7
x = 3
Putting value of x in eq2
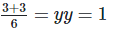
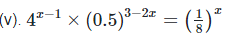
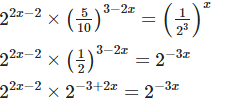
2x−2−3+2x = −3x [By equating exponents]
4x+3x = 5
7x = 5
x = 5/7
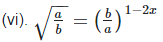
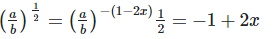[By equating exponents]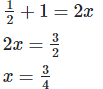
17. If a and b are distinct positive primes such that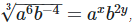 
find x and y
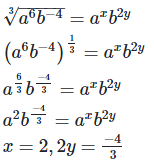
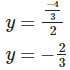
18.If a and b are different positive primes such that
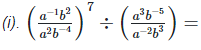axby find x and y
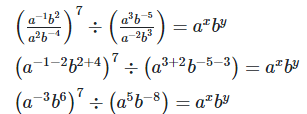
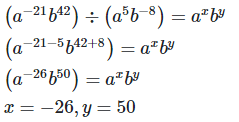
(ii) (a+b)−1(a−1+b−1) = axby,find x and y
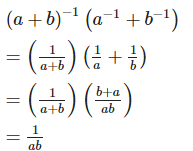
=(ab)−1 = a−1b−1
By equating exponents
x = −1,y = −1
Therefore x+y+2 = −1−1+2 = 0
19. If 2x×3y×5z = 2160 , find x,y and z. Hence compute the value of 3x×2−y×5−z
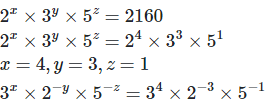
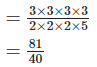
20. If 1176 = 2a×3b×7c, find the values of a,b and c. Hence compute the value of 2a×3b×7−c as a fraction
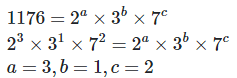
We have to find the value of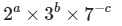 
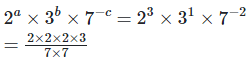
= 24/49
21. Simplify
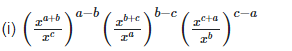
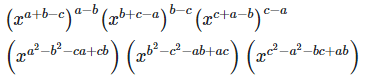
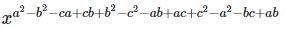
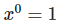
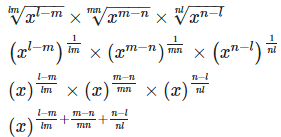
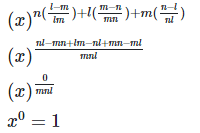
22. Show that
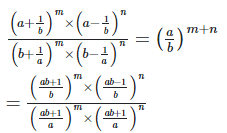
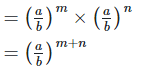
Hence LHS = RHS
23.
(i)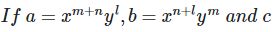 
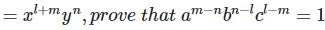
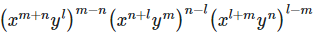
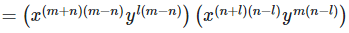
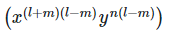
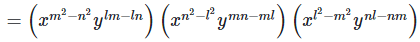
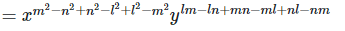
= x0 y0
= 1
The document RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics is a part of the Class 9 Course RD Sharma Solutions for Class 9 Mathematics.
All you need of Class 9 at this link: Class 9
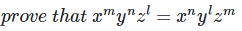
FAQs on RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are exponents and how are they used in real numbers? |  |
Ans. Exponents are a way to represent repeated multiplication of a number by itself. In real numbers, exponents are used to express very large or very small numbers in a concise and convenient form. For example, the number 10 raised to the power of 3 (10^3) represents 10 multiplied by itself three times (10 x 10 x 10), which is equal to 1000.
| 2. How do exponents affect the value of a real number? | |
Ans. Exponents can significantly impact the value of a real number. When the exponent is positive, it indicates repeated multiplication and results in a larger value. Conversely, when the exponent is negative, it indicates repeated division and leads to a smaller value. For instance, 2^3 equals 2 x 2 x 2, which is 8, while 2^-3 equals 1/(2 x 2 x 2), which is 1/8 or 0.125.
| 3. What is the significance of the exponent 0 in real numbers? | |
Ans. The exponent 0 in real numbers has a special significance. Any non-zero number raised to the power of 0 is always equal to 1. For example, 5^0 is equal to 1, as there are no repeated multiplications involved. This property is based on the idea that any number divided by itself is equal to 1.
| 4. How can exponents be used to simplify calculations with real numbers? | |
Ans. Exponents can simplify calculations with real numbers by reducing the number of operations required. Instead of performing repeated multiplications or divisions, we can use exponents to represent the same calculations more concisely. For instance, instead of calculating 2 x 2 x 2 x 2, we can simply write 2^4. This simplifies calculations and makes them easier to solve.
| 5. Can exponents be used with all types of real numbers? | |
Ans. Exponents can be used with all types of real numbers, including both integers and fractions. While exponents are commonly associated with positive whole numbers, they can also be negative, zero, or fractions. This flexibility allows us to represent a wide range of values and perform various mathematical operations using exponents.
Related Exams
About this Document
|
4.81/5 Rating |
|
Dec 23, 2024 Last updated |
Document Description: RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths for Class 9 2024 is part of RD Sharma Solutions for Class 9 Mathematics preparation.
The notes and questions for RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths have been prepared according to the Class 9 exam syllabus. Information about RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths covers topics
like and RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths Example, for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths.
Introduction of RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths in English is available as part of our RD Sharma Solutions for Class 9 Mathematics
for Class 9 & RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths in Hindi for RD Sharma Solutions for Class 9 Mathematics course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics
Description
Full syllabus notes, lecture & questions for RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics - Class 9 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 9 Mathematics | Best notes, free PDF download
Information about RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths
In this doc you can find the meaning of RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths defined & explained in the simplest way possible. Besides explaining types of
RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths tests, examples and also practice Class 9
tests
|
Explore Courses for Class 9 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Class 9
,ppt
,Semester Notes
,(Part - 2)
,Maths | RD Sharma Solutions for Class 9 Mathematics
,past year papers
,Exam
,Extra Questions
,mock tests for examination
,Previous Year Questions with Solutions
,Class 9
,RD Sharma Solutions Ex-2.2
,Summary
,study material
,Class 9
,RD Sharma Solutions Ex-2.2
,Viva Questions
,Objective type Questions
,video lectures
,Exponents Of Real Numbers
,Maths | RD Sharma Solutions for Class 9 Mathematics
,Sample Paper
,Exponents Of Real Numbers
,shortcuts and tricks
,(Part - 2)
,Important questions
,MCQs
,practice quizzes
,Maths | RD Sharma Solutions for Class 9 Mathematics
,(Part - 2)
,RD Sharma Solutions Ex-2.2
,Exponents Of Real Numbers
,Free
;
Additional Information about RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths for Class 9 Preparation
RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths Free PDF Download
The RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths now and kickstart your journey towards success in the Class 9 exam.
Importance of RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths
The importance of RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths Notes
RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths Notes on EduRev are your ultimate resource for success.
RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths Class 9 Questions
The "RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths on the App
Students of Class 9 can study RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of RD Sharma Solutions Ex-2.2, (Part - 2), Exponents Of Real Numbers, Class 9, Maths is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup