Class 9 Exam > Class 9 Notes > RD Sharma Solutions for Class 9 Mathematics > RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths
Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. Define cumulative frequency distribution.
Solution 1: Cumulative frequency distribution:
A table which displays the manner in which cumulative frequencies are distributed over various classes is called a cumulative frequency distribution or cumulative frequency distribution table.
Q2. Explain the difference between a frequency distribution and a cumulative frequency distribution.
Solution 2:
Frequency table or frequency distribution is a method to represent raw data in the form from which one can easily understand the information contained in a raw data, where as a table which plays the manner in which cumulative frequencies are distributed over various classes is called a cumulative frequency distribution.
Q3. The marks scored by 55 students in a test are given below:
| Marks | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 - 30 | 30 - 35 |
| No. of students | 2 | 6 | 13 | 17 | 11 | 4 | 2 |
Prepare a cumulative frequency table
Solution 3:
| Marks | No. of students | Marks | Cumulative Frequency |
| 0 - 5 | 2 | Less than 5 | 2 |
| 5 - 10 | 6 | Less than 10 | 8 |
| 10 - 15 | 13 | Less than 15 | 21 |
| 15 - 20 | 17 | Less than 20 | 38 |
| 20 - 25 | 11 | Less than 25 | 49 |
| 25 - 30 | 4 | Less than 30 | 53 |
| 30 - 35 | 2 | Less than 35 | 55 |
| N = 55 |
Q4. Following are the ages of 360 patients getting medical treatment in a hospital on a day.
| Age(in years) | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 |
| No of patients | 90 | 50 | 60 | 80 | 50 | 30 |
Construct a cumulative frequency table.
Solution 4:
| Age (in years) | No. of students | Marks | Cumulative Frequency |
| 10 - 20 | 90 | Less than 20 | 90 |
| 20 - 30 | 50 | Less than 30 | 140 |
| 30 - 40 | 60 | Less than 40 | 200 |
| 40 - 50 | 80 | Less than 50 | 280 |
| 50 - 60 | 50 | Less than 60 | 330 |
| 60 - 70 | 30 | Less than 70 | 360 |
| N = 360 |
Q5. The water bills (in rupees) of 32 houses in a certain street for the period 1.198 to 31.398 are given below:
56,43,32,38,56,24,68,85,52,47,35,58,63,74,27,84,69,35,44,75,55,30,54,65,45,67,95,72,43,65,35,69.
Tabulate the data and present the data as a cumulative frequency table using 70 - 79 as one of the class intervals.
Solution 5:
The minimum bill is Rs 24
The maximum bill is Rs 95
Range = Maximum bill - Minimum bill = 95 - 24 = 71
Given class interval is 70 - 79.So, class size = 79 - 70 = 9
Therefore number of classes =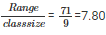 
Number of classes = 8
The cumulative frequency distribution is as follows:
| Bills | No. of houses(frequency) | Cumulative frequency |
| 16 - 25 | 1 | 1 |
| 25 - 34 | 3 | 4 |
| 34 - 43 | 5 | 9 |
| 43 - 52 | 4 | 13 |
| 52 - 61 | 7 | 20 |
| 61 - 70 | 6 | 26 |
| 70 - 79 | 3 | 29 |
| 79 - 88 | 2 | 31 |
| 88 - 97 | 1 | 32 |
Q6.The number of books in different shelves of a library is as follows:
30, 32, 28, 24, 20, 25, 38, 37, 40, 45, 16, 20
19, 24, 27, 30, 32, 34, 35, 42, 27, 28, 19, 34
38, 39, 42, 29, 24, 27, 22, 29, 31, 19, 27, 25
28, 23, 24, 32, 34, 18, 27, 25, 37, 31, 24, 23
43, 32, 28, 31, 24, 23, 26, 36, 32, 29, 28, 21.
Prepare a cumulative frequency distribution table using 45 - 49 as the last class - interval.
Solution 6:
The minimum number of bookshelves is 16
and maximum number of bookshelves is 45
Range = Maximum book shelves - Minimum book shelves = 45 - 16 = 29
Given class interval is 45 - 49.So, class size = 49 - 45 = 4
Therefore number of classes =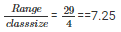 
Number of classes = 8
The cumulative frequency distribution is as follows:
| No of books | No. of shelves(frequency) | Cumulative frequency |
| 13 - 17 | 1 | 1 |
| 17 - 21 | 6 | 7 |
| 21 - 25 | 11 | 18 |
| 25 - 29 | 15 | 33 |
| 29 - 33 | 12 | 45 |
| 33 - 37 | 5 | 50 |
| 37 - 41 | 6 | 56 |
| 41 - 45 | 3 | 59 |
| 45 - 49 | 1 | 60 |
Q7. Given below are the cumulative frequencies showing the weights of 685 students of a school. Prepare a frequency distribution table.
| Weight(in kg) | No. of students |
| Below 30 | 0 |
| Below 30 | 24 |
| Below 35 | 78 |
| Below 40 | 183 |
| Below 45 | 294 |
| Below 50 | 408 |
| Below 55 | 543 |
| Below 60 | 621 |
| Below 65 | 674 |
| Below 70 | 685 |
Solution 7:
| Weight(in kg) | No. of students | Class interval | frequency |
| Below 30 | 24 | 25 - 30 | 24 - 0 = 24 |
| Below 35 | 78 | 30 - 35 | 78 - 24 = 54 |
| Below 40 | 183 | 35 - 40 | 183 - 78 = 105 |
| Below 45 | 294 | 40 - 45 | 294 - 183 = 111 |
| Below 50 | 408 | 45 - 50 | 408 - 294 = 114 |
| Below 55 | 543 | 50 - 55 | 543 - 408 = 135 |
| Below 60 | 621 | 55 - 60 | 621 - 543 = 78 |
| Below 65 | 674 | 60 - 65 | 671 - 621 = 53 |
| Below 70 | 685 | 65 - 70 | 685 - 671 = 11 |
Q8. The following cumulative frequency distribution table shows the daily electricity consumption (in KW) of 40 factories in an industrial state.
| Consumption(in KW) | No. of factories |
| Below 240 | 1 |
| Below 270 | 4 |
| Below 300 | 8 |
| Below 330 | 24 |
| Below 360 | 33 |
| Below 390 | 38 |
| Below 420 | 40 |
(1) Represent this as a frequency distribution table.
(2)Prepare a cumulative frequency table.
Solution 8:
(1)
| Consumption(in KW) | No. of factories | Class interval | Frequency |
| Below 240 | 1 | 0 - 240 | 1 |
| Below 270 | 4 | 240 - 270 | 4 - 1 = 3 |
| Below 300 | 8 | 270 - 300 | 8 - 4 = 4 |
| Below 330 | 24 | 300 - 330 | 24 - 8 = 16 |
| Below 360 | 33 | 330 - 360 | 33 - 24 = 9 |
| Below 390 | 38 | 360 - 390 | 38 - 33 = 5 |
| Below 420 | 40 | 390 - 420 | 40 - 38 = 2 |
(2)
| Class interval | Frequency | Consumption(in KW) | No. of factories |
| 0 - 240 | 1 | More than 0 | 40 |
| 240 - 270 | 3 | More than 240 | 40 - 1 = 39 |
| 270 - 300 | 4 | More than 270 | 39 - 3 = 36 |
| 300 - 330 | 16 | More than 300 | 36 - 4 = 32 |
| 330 - 360 | 9 | More than 330 | 32 - 16 = 16 |
| 360 - 390 | 5 | More than 360 | 16 - 9 = 7 |
| 390 - 420 | 2 | More than 390 | 7 - 5 = 2 |
| More than 420 | 2 - 2 = 0 | ||
| N = 40 |
Q9. Given below is a cumulative frequency distribution table showing ages of the people living in a locality:
| Age in years | No. of years |
| Above 108 | 0 |
| Above 96 | 1 |
| Above 84 | 3 |
| Above 72 | 5 |
| Above 60 | 20 |
| Above 48 | 158 |
| Above 36 | 427 |
| Above 24 | 809 |
| Above 12 | 1026 |
| Above 0 | 1124 |
Prepare a frequency distribution table.
Solution 9:
| Age (in years) | No. of persons | Class interval | Frequency |
| Above 0 | 1124 | 0 - 12 | 1124 - 1026 = 98 |
| Above 12 | 1026 | 12 - 24 | 217 |
| Above 24 | 809 | 24 - 36 | 382 |
| Above 36 | 427 | 36 - 48 | 269 |
| Above 38 | 158 | 48 - 60 | 138 |
| Above 60 | 20 | 60 - 72 | 15 |
| Above 72 | 5 | 72 - 84 | 5 - 3 = 2 |
| Above 84 | 3 | 84 - 96 | 3 - 1 = 2 |
| Above 96 | 3 | 96 - 108 | 1 - 0 = 1 |
The document Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics is a part of the Class 9 Course RD Sharma Solutions for Class 9 Mathematics.
All you need of Class 9 at this link: Class 9
FAQs on Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of tabular representation of statistical data? |  |
Ans. Tabular representation of statistical data is important because it helps in organizing and summarizing large amounts of data in a systematic manner. It allows for easy comparison and analysis of different sets of data. Additionally, it helps in identifying patterns, trends, and outliers in the data, which is crucial for making informed decisions and drawing meaningful conclusions.
| 2. How can I construct a frequency distribution table from raw data? | |
Ans. To construct a frequency distribution table from raw data, follow these steps:
1. Determine the range of the data by subtracting the smallest value from the largest value.
2. Decide on the number of classes or intervals you want to divide the data into. Generally, it is recommended to have around 5-15 classes.
3. Calculate the width of each class by dividing the range by the number of classes and rounding it off to a convenient number.
4. Create a table with columns for the classes, frequencies, and cumulative frequencies.
5. Start with the lowest value and assign each data point to the respective class interval.
6. Count the number of data points in each class and record the frequencies in the table.
7. Calculate the cumulative frequencies by adding up the frequencies from the first class to each subsequent class.
8. Finally, you have your frequency distribution table ready for further analysis.
| 3. How can I calculate the mean using a frequency distribution table? | |
Ans. To calculate the mean using a frequency distribution table, use the following steps:
1. Multiply each class midpoint by its corresponding frequency.
2. Sum up the products obtained in step 1.
3. Divide the sum by the total number of data points (sum of frequencies).
4. The result is the mean or average value of the data.
| 4. What is the difference between a class interval and class frequency? | |
Ans. A class interval refers to the range of values that are grouped together in a frequency distribution table. It is represented by the lower class limit and the upper class limit. For example, if the class interval is 20-30, it means that all values between 20 and 30 (including 20 but excluding 30) are grouped together.
On the other hand, class frequency refers to the number of data points that fall within a particular class interval. It represents the count or frequency of occurrence of values within that interval. It is recorded in the frequency column of a frequency distribution table.
| 5. How can I calculate the median from a grouped frequency distribution table? | |
Ans. To calculate the median from a grouped frequency distribution table, follow these steps:
1. Find the cumulative frequency just greater than or equal to (n/2), where n is the total number of data points.
2. Identify the corresponding class interval.
3. Use the formula:
Median = L + ((n/2 - CF) * h) / f
where L is the lower class limit of the median class interval, CF is the cumulative frequency of the class interval preceding the median class, h is the class width, and f is the frequency of the median class interval.
4. Substitute the values from the table into the formula to calculate the median.
Related Exams
About this Document
|
4.60/5 Rating |
|
Nov 08, 2024 Last updated |
Document Description: RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths for Class 9 2024 is part of RD Sharma Solutions for Class 9 Mathematics preparation.
The notes and questions for RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths have been prepared according to the Class 9 exam syllabus. Information about RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths covers topics
like and RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths Example, for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths.
Introduction of RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths in English is available as part of our RD Sharma Solutions for Class 9 Mathematics
for Class 9 & RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths in Hindi for RD Sharma Solutions for Class 9 Mathematics course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics
Description
Full syllabus notes, lecture & questions for Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics - Class 9 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 9 Mathematics | Best notes, free PDF download
Information about RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths
In this doc you can find the meaning of RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths defined & explained in the simplest way possible. Besides explaining types of
RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths tests, examples and also practice Class 9
tests
|
Explore Courses for Class 9 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Sample Paper
,Class 9
,Objective type Questions
,video lectures
,Viva Questions
,MCQs
,Class 9
,Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics
,shortcuts and tricks
,Semester Notes
,Summary
,Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics
,Exam
,Extra Questions
,Class 9
,past year papers
,Free
,Ex-22.2
,Important questions
,Tabular Representation Of Statistical Data
,Tabular Representation Of Statistical Data
,study material
,Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics
,Tabular Representation Of Statistical Data
,Ex-22.2
,mock tests for examination
,practice quizzes
,Previous Year Questions with Solutions
,ppt
,Ex-22.2
;
Additional Information about RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths for Class 9 Preparation
RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths Free PDF Download
The RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths now and kickstart your journey towards success in the Class 9 exam.
Importance of RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths
The importance of RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths Notes
RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths Notes on EduRev are your ultimate resource for success.
RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths Class 9 Questions
The "RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths on the App
Students of Class 9 can study RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of RD Sharma Solutions -Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup