Class 9 Exam > Class 9 Notes > RD Sharma Solutions for Class 9 Mathematics > RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths
RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q.1: If the heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm respectively. Find the mean height.
SOLUTION :
Given : the heights of 5 persons are 140 cm , 150 cm , 152 cm , 158 cm and 161 cm
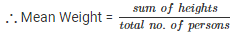
Q 2 . Find the mean of 994 , 996 , 998 , 1000 , 1002.
SOLUTION :
Given :
Numbers are 994 , 996 , 998 , 1000 , 1002.
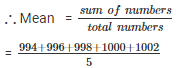
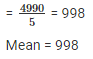
Q 3 . Find the mean of first five natural numbers.
SOLUTION :
The first five odd numbers are 1 , 2 , 3 , 4 , 5.
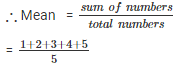
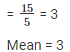
Q 4 . Find the mean of all factors of 10.
SOLUTION :
All factors of 6 are 1 , 2 , 5 , 10.
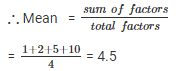
Mean = 4.5
Q 5 . Find the mean of first ten even natural numbers.
SOLUTION :
The first five even natural numbers are 2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , 18 , 20
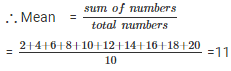
Mean = 11
Q 6 . Find the mean of x , x + 2 , x + 4 , x + 6 , x + 8.
SOLUTION :
Numbers are x , x + 2 , x + 4 , x + 6 , x + 8.
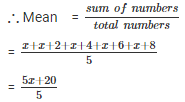
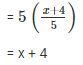
Q 7. Find the mean of first five multiples of 3.
SOLUTION :
First five multiples of 3 are 3 , 6 , 9 , 12 , 15.
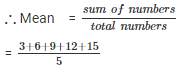
= 9
Mean = 9
Q 8 . Following are the weights of 10 new born babies in a hospital on a particular day : 3.4 , 3 .6 , 4.2 , 4.5 , 3.9 , 4.1 , 3.8 , 4.5 , 4.4 , 3.6 (in kg). Find the mean.
SOLUTION : The weights (in kg) of 10 new born babies are : 3.4 , 3 .6 , 4.2 , 4.5 , 3.9 , 4.1 , 3.8 , 4.5 , 4.4 , 3.6
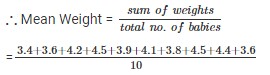
= 4 kg
Q 9 . The percentage marks obtained by students of a class in mathematics are as follows: 64 , 36 , 47 , 23 , 0 , 19 , 81 , 93 , 72 , 35 , 3 , 1 .Find their mean.
SOLUTION :
The percentage marks obtained by students are 64 , 36 , 47 , 23 , 0 , 19 , 81 , 93 , 72 , 35 , 3 , 1
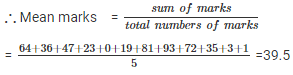
Mean Marks = 39.5
Q 10. The numbers of children in 10 families of a locality are 2 , 4 , 3 , 4 , 2 , 3 , 5 , 1 , 1 , 5 . Find the number of children per family.
SOLUTION :
The numbers of children in 10 families are : 2 , 4 , 3 , 4 , 2 , 3 , 5 , 1 , 1 , 5
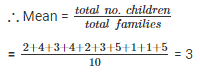
Q 11 . If M is the mean of x1,x2,x3,x4,x5 and x6 , Prove that
(x1−M)+(x2−M)+(x3−M)+(x4−M)+(x5−M)+(x6−M) = 0.
SOLUTION :
Let M be the mean of x1,x2,x3,x4,x5 and x6
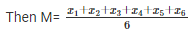
= x1+x2+x3+x4+x5+x6 = 6M
To Prove :- (x1−M)+(x2−M)+(x3−M)+(x4−M)+(x5−M)+(x6−M) = 0.
Proof :- L . H . S
= (x1−M)+(x2−M)+(x3−M)+(x4−M)+(x5−M)+(x6−M)
= (x1+x2+x3+x4+x5+x6)−(M+M+M+M+M+M)
= 6M – 6M
= 0
= R . H . S
Q 12 . Duration of sunshine(in hours) in Amritsar for first 10 days of August 1997 as reported by the Meterological Department are given as follows : 9.6 , 5.2 , 3.5 , 1.5 , 1.6 , 2.4 , 2.6 , 8.4 , 10.3 , 10.9
1. Find the mean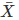 
2.Verify that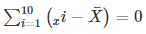 
SOLUTION :
Duration of sunshine (in hours ) for 10 days are =9.6 , 5.2 , 3.5 , 1.5 , 1.6 , 2.4 , 2.6 , 8.4 , 10.3 , 10.9
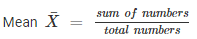
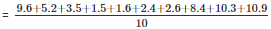
= 56/10 = 5.6
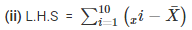
= (9.6−5.6)+(5.2−5.6)+(3.5−5.6)+(1.5−5.6)+(1.6−5.6)+(2.4−5.6)+(2.6−5.6)+(8.4−5.6)+(10.3−5.6)+(10.9−5.6)
= 4 – 0.4 – 2.1 – 4.1 – 4 – 3.2 – 3 + 2.8 + 4.7 + 5.3
= 16.8 – 16.8 = 0
= R.H.S
The document RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics is a part of the Class 9 Course RD Sharma Solutions for Class 9 Mathematics.
All you need of Class 9 at this link: Class 9
FAQs on RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are measures of central tendency in statistics? |  |
Ans. Measures of central tendency are statistical measures that represent the center or typical value of a dataset. These measures include the mean, median, and mode. The mean is the average value of the dataset, the median is the middle value when the data is arranged in ascending or descending order, and the mode is the value that appears most frequently in the dataset.
| 2. How is the mean calculated for a given dataset? | |
Ans. The mean is calculated by summing up all the values in the dataset and dividing the sum by the total number of values. Mathematically, the formula for calculating the mean is:
Mean = (sum of all values) / (total number of values)
For example, if we have a dataset {5, 7, 9, 11, 13}, the mean would be calculated as (5+7+9+11+13)/5 = 9.
| 3. What is the median and how is it determined in a dataset? | |
Ans. The median is the middle value in a dataset when the data is arranged in ascending or descending order. To determine the median, the data is first arranged in order, and then the middle value is identified. If the dataset has an odd number of values, the middle value is the median. If the dataset has an even number of values, the median is the average of the two middle values.
For example, in the dataset {5, 7, 9, 11, 13}, the median would be 9. In the dataset {5, 7, 9, 11, 13, 15}, the median would be (9+11)/2 = 10.
| 4. How is the mode determined in a dataset? | |
Ans. The mode in a dataset is the value that appears most frequently. To determine the mode, we count the frequency of each value in the dataset and identify the value with the highest frequency. It is possible for a dataset to have multiple modes if multiple values have the same highest frequency.
For example, in the dataset {5, 7, 9, 9, 11, 13, 13, 13}, the mode would be 13 as it appears three times, which is the highest frequency.
| 5. How do measures of central tendency help in understanding a dataset? | |
Ans. Measures of central tendency provide valuable information about the typical or central value of a dataset. The mean, median, and mode help in understanding the average, middle, and most frequently occurring values, respectively. These measures help in summarizing the data, making comparisons, and drawing conclusions. They are also useful in identifying outliers or extreme values that may impact the overall interpretation of the dataset.
Related Exams
About this Document
|
4.78/5 Rating |
|
Nov 25, 2024 Last updated |
Document Description: RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths for Class 9 2024 is part of RD Sharma Solutions for Class 9 Mathematics preparation.
The notes and questions for RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths have been prepared according to the Class 9 exam syllabus. Information about RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths covers topics
like and RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths Example, for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths.
Introduction of RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths in English is available as part of our RD Sharma Solutions for Class 9 Mathematics
for Class 9 & RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths in Hindi for RD Sharma Solutions for Class 9 Mathematics course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics
Description
Full syllabus notes, lecture & questions for RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics - Class 9 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 9 Mathematics | Best notes, free PDF download
Information about RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths
In this doc you can find the meaning of RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths defined & explained in the simplest way possible. Besides explaining types of
RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths tests, examples and also practice Class 9
tests
|
Explore Courses for Class 9 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Class 9
,RD Sharma Solutions Ex-24.1
,(Part - 1)
,RD Sharma Solutions Ex-24.1
,shortcuts and tricks
,Maths | RD Sharma Solutions for Class 9 Mathematics
,Objective type Questions
,Maths | RD Sharma Solutions for Class 9 Mathematics
,Measures Of Central Tendency
,ppt
,(Part - 1)
,Maths | RD Sharma Solutions for Class 9 Mathematics
,RD Sharma Solutions Ex-24.1
,(Part - 1)
,Semester Notes
,Viva Questions
,study material
,practice quizzes
,Sample Paper
,Summary
,Important questions
,Class 9
,Free
,Measures Of Central Tendency
,past year papers
,Previous Year Questions with Solutions
,video lectures
,Measures Of Central Tendency
,mock tests for examination
,Exam
,Extra Questions
,Class 9
,MCQs
;
Additional Information about RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths for Class 9 Preparation
RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths Free PDF Download
The RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths now and kickstart your journey towards success in the Class 9 exam.
Importance of RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths
The importance of RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths Notes
RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths Notes on EduRev are your ultimate resource for success.
RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths Class 9 Questions
The "RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths on the App
Students of Class 9 can study RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of RD Sharma Solutions Ex-24.1, (Part - 1), Measures Of Central Tendency, Class 9, Maths is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup