RD Sharma Solutions Ex-25.1, (Part - 1), Probability, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. A coin is tossed 1000 times with the following sequence: Head: 455, Tail = :545. Compute the probability of each event
Answer: It is given that the coin is tossed 1000 times. The number of trials is 1000
Let us denote the event of getting head and of getting tails be E and F respectively. Then
Number of trials in which the E happens = 455
So, Probability of 
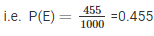
Similarity, the probability of the event getting a tail 
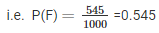
Q2. Two coins are tossed simultaneously 500 times with the following frequencies of different outcomes:
TWO HEADS: 95 times
ONE HEADS: 290 times
NO HEADS: 115 times
Find the probability of occurrence of each of these events
Answer:
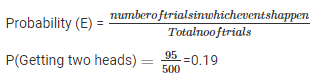
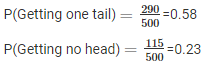
Q3. Three coins are tossed simultaneously 100 times with the following frequencies of different outcomes:
| OUTCOME | NO HEAD | ONE HEAD | TWO HEAD | THREE HEAD |
| FREQUENCY | 14 | 38 | 36 | 12 |
If the three coins are tossed simultaneously again, compute the probability of:
1. heads coming up
2. heads coming up
3. At least one Head coming up
4. Getting more Tails than Heads
5. Getting more heads than tails
ANS:
1: Probability of 2 Heads coming up 
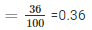
2. Probability of 3 Heads coming up 
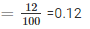
3. Probability of at least one head coming up 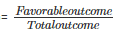

4. Probability of getting more Heads than Tails 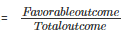
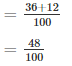
5. Probability of getting more tails than heads 
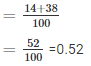
Q4. 1500 families with 2 children were selected randomly, and the following data were recorded:
| No of girls in a family | 0 | 1 | 2 |
| No of girls | 211 | 814 | 475 |
If a family is chosen at random, compute the probability that it has:
1. No girl
2. 1 girl
3. 2 girls
4. At most one girl
5. More girls than boys
Answer
1. Probability of having no girl in a family 
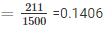
2. Probability of having 1 girl in a family 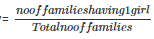

3. Probability of having 2 girls in a family 
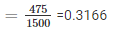
4. Probability of having at the most one girl 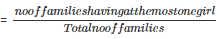

5. Probability of having more girls than boys 
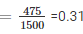
Q5. In a cricket match, a batsman hits a boundary 6 times out of 30 balls he plays. Find the probability that:
1. He hit a boundary
2. He did not hit a boundary.
Answer
Number of times the batsman hits a boundary= 6
Total number of balls played= 30
Number of times the batsman did not hit a boundary= 30-6 = 24
1. Probability that the batsman hits a boundary 
= 6/30
= 1/5
2. Probability that the batsman does not hit a boundary

= 24/30
= 4/5
Q6. The percentage of marks obtained by a student in the monthly unit tests are given below:
| UNIT TEST | I | II | III | IV | V |
| PERCENTAGE OF MARK OBTAINED | 69 | 71 | 73 | 68 | 76 |
Find the probability that the student gets
1. More than 70% marks
2. Less than 70% marks
3. A distinction
Answer:
1: Let E be the event of getting more than 70% marks
No of times E happens=3
Probability(Getting more than 70%) 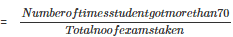
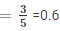
2. Let F be the event of getting less than 70% marks
No of times F happen = 2
Probability(Getting less than 70%) 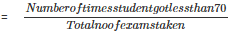
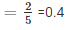
3. Let G be the event of getting distinction
No of times G happen = 1
Probability(Getting distinction) = 
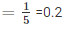
Q7. To know the opinion of the students about Mathematics, a survey of 200 students were conducted. The data was recorded in the following table
| Opinion | Like | Dislike |
| Number of students | 135 | 65 |
Find the probability that student chosen at random:
1. Likes Mathematics
2. Does not like it.
Answer
1. Probability that a student likes mathematics 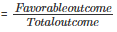

2. Probability that a student does not like mathematics 
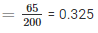
FAQs on RD Sharma Solutions Ex-25.1, (Part - 1), Probability, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of studying probability in Class 9 Mathematics? |  |
| 2. What are the basic concepts of probability? |  |
| 3. How do you calculate the probability of an event? |  |
| 4. What is the difference between experimental probability and theoretical probability? |  |
| 5. How is probability used in real-life situations? |  |





















