RD Sharma Solutions Ex-3.2, Rationalisation, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
1. Rationalize the denominator of each of the following:
(i) 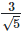
(ii) 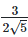
(iii) 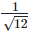
(iv) 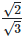
(v) 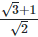
(vi) 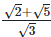
(vii) 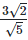
Solution: (i) 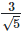 For rationalizing the denominator, multiply both numerator and denominator with
For rationalizing the denominator, multiply both numerator and denominator with 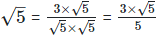
(ii) 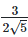 For rationalizing the denominator, multiply both numerator and denominator with
For rationalizing the denominator, multiply both numerator and denominator with 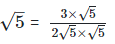
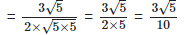
(iii) 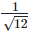 For rationalizing the denominator, multiply both numerator and denominator with
For rationalizing the denominator, multiply both numerator and denominator with 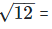
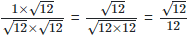
(iv) 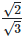 For rationalizing the denominator, multiply both numerator and denominator with
For rationalizing the denominator, multiply both numerator and denominator with 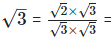
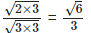
(v) 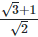 For rationalizing the denominator, multiply both numerator and denominator with
For rationalizing the denominator, multiply both numerator and denominator with 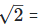
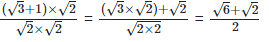
(vi) 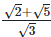 For rationalizing the denominator, multiply both numerator and denominator with
For rationalizing the denominator, multiply both numerator and denominator with 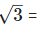
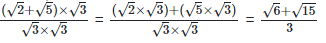
(vii) 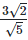 For rationalizing the denominator, multiply both numerator and denominator with
For rationalizing the denominator, multiply both numerator and denominator with 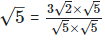
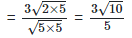
2. Find the value to three places of decimals of each of the following. It is given that  = 1.414,
= 1.414, = 1.732,
= 1.732,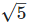 = 2.236,
= 2.236, 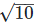 = 3.162.
= 3.162.
(i) 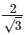
(ii) 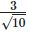
(iii) 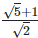
(iv) 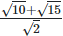
(v) 
(vi) 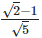
Solution: Given,  = 1.414,
= 1.414, = 1.732,
= 1.732,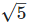 = 2.236,
= 2.236, 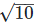 = 3.162.
= 3.162.
(i) 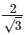 Rationalizing the denominator by multiplying both numerator and denominator with
Rationalizing the denominator by multiplying both numerator and denominator with 
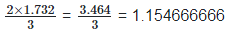
(ii) 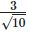 Rationalizing the denominator by multiplying both numerator and denominator with
Rationalizing the denominator by multiplying both numerator and denominator with 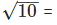
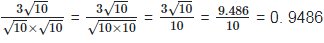
(iii) 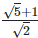 Rationalizing the denominator by multiplying both numerator and denominator with
Rationalizing the denominator by multiplying both numerator and denominator with 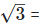
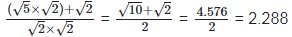
(iv) 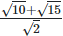 Rationalizing the denominator by multiplying both numerator and denominator with
Rationalizing the denominator by multiplying both numerator and denominator with 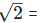
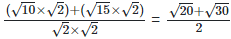
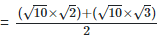
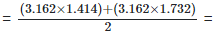
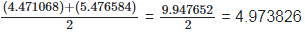
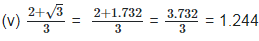
(vi) 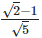 Rationalizing the denominator by multiplying both numerator and denominator with
Rationalizing the denominator by multiplying both numerator and denominator with 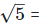
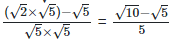
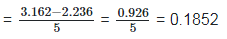
3. Express each one of the following with rational denominator:
(i) 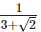
(ii) 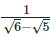
(iii) 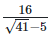
(iv) 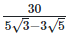
(v) 
(vi) 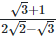
(vii) 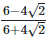
(viii) 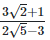
(ix) 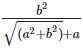
Solution: (i) 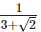 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 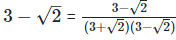
As we know, (a + b) (a - b) = (a2−b2) 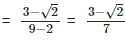
(ii) 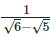 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 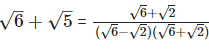
As we know, (a + b) (a - b) = (a2 − b2) 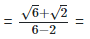
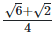
(iii) 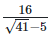 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 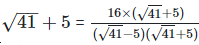
As we know, (a + b) (a - b) = (a2−b2) 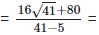
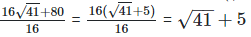
(iv) 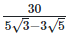 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 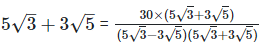
As we know, (a + b) (a - b) = (a2−b2) = 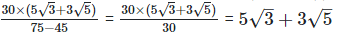
(v)  Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 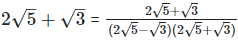
As we know, (a + b) (a - b) = (a2−b2) = 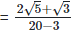
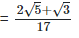
(vi) 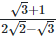 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 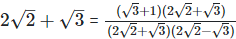
As we know, (a + b) (a - b) = (a2−b2) = 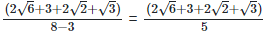
(vii) 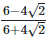 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 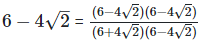
As we know, (a + b) (a - b) = (a2−b2) 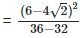 As we know , (a - b)2 = (a2−2×a×b+b2)
As we know , (a - b)2 = (a2−2×a×b+b2) 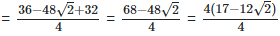
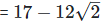
(viii) 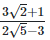 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 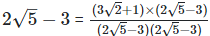
As we know, (a + b) (a - b) = (a2−b2) = 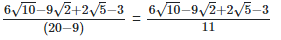
(ix) 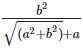 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 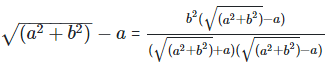
As we know, (a + b) (a - b) = (a2−b2) 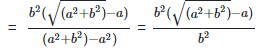
4. Rationalize the denominator and simplify:
(i) 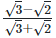
(ii) 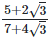
(iii) 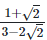
(iv) 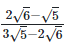
(v) 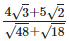
(vi) 
Solution: (i) 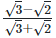 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 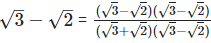
As we know, (a + b) (a - b) 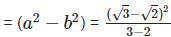 As we know , (a - b) 2 = (a2−2×a×b+b2)
As we know , (a - b) 2 = (a2−2×a×b+b2) 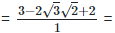
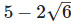
(ii) 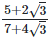 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 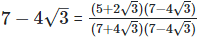
As we know, (a + b) (a - b) = (a2−b2) = 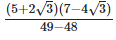
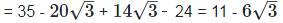
(iii) 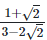 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 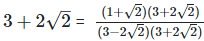
As we know, (a + b) (a - b) = (a2−b2) 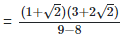
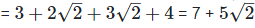
(iv) 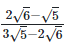 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 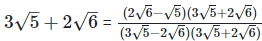
As we know, (a + b) (a - b) = (a2−b2) = 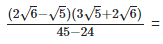
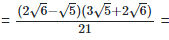

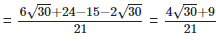
(v) 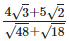 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 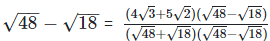
As we know, (a + b) (a - b) = (a2−b2) = 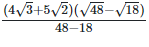
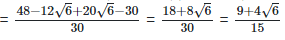
(vi)  Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 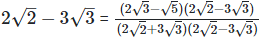
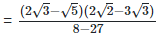
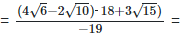
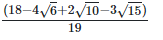
5. Simplify:
(i) 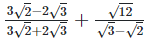
(ii) 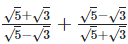
(iii) 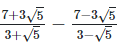
(iv) 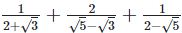
(v) 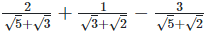
Solution: (i) 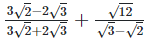 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 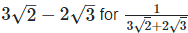 and the rationalizing factor
and the rationalizing factor 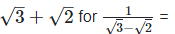

Now, (a + b) (a - b) = (a2−b2) = 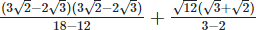
As we know , (a - b)2 = (a2−2×a×b+b2) = 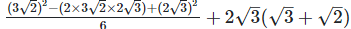
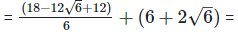
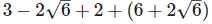
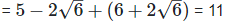
(ii) 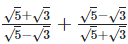 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 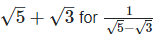 and the rationalizing factor
and the rationalizing factor 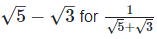 =
= 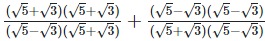
Now as we know, (a + b) (a - b) = (a2−b2), (a - b)2 = (a2−2×a×b+b2) and (a+b)2 = (a2+2×a×b+b2)
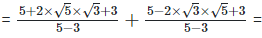
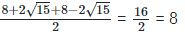
(iii) 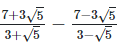 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 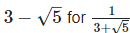 and the rationalizing factor
and the rationalizing factor 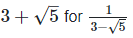
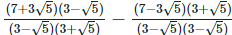
Now as we know, (a + b) (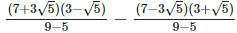
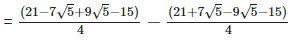
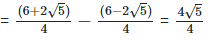
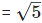
(iv) 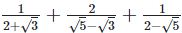 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 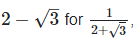 the rationalizing
the rationalizing 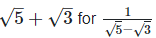
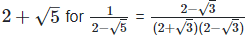
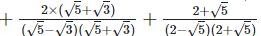
Since, (a + b) (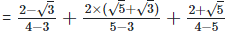
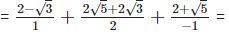
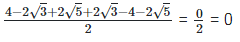
(v) 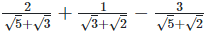 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 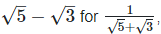 the rationalizing factor
the rationalizing factor 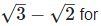
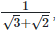 and the rationalizing factor
and the rationalizing factor 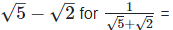
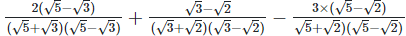
Since, (a + b) (a - b) = (a2−b2) = 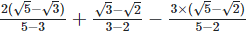
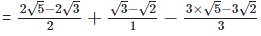
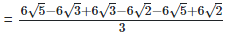
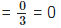
6. In each of the following determine rational numbers a and b:
(i) 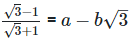
(ii) 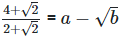
(iii) 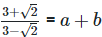
(iv) 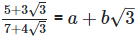
(v) 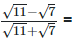
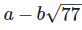
(vi) 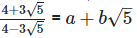
Solution: (i) Given, 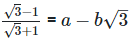 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
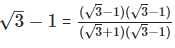
As we know, (a + b) (a - b) = (a2−b2) 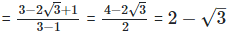
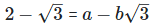
On comparing the rational and irrational parts of the above equation, we get, a = 2 and b = 1
(ii) 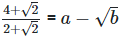 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 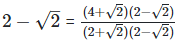
As we know, (a + b) (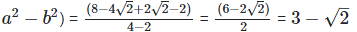
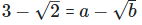
On comparing the rational and irrational parts of the above equation, we get,
a = 3 and b = 2
(iii) 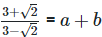 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 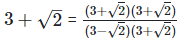
As we know, (a + b) (
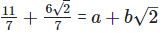
On comparing the rational and irrational parts of the above equation, we get,
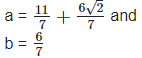
(iv) 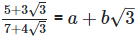 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 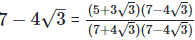
As we know, (a + b) (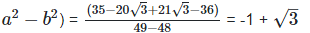
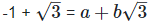
On comparing the rational and irrational parts of the above equation, we get,
a = -1 and
b = 1
(v) 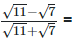
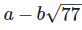 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 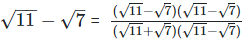
As we know, (a + b) (a - b) = (a2−b2) = 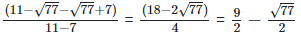
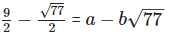
On comparing the rational and irrational parts of the above equation, we get,
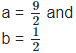
(vi) 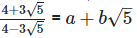 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 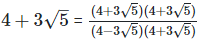
As we know, (a + b) (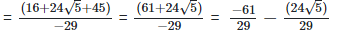
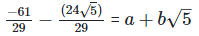
On comparing the rational and irrational parts of the above equation, we get,
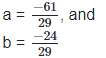
7. If x = 2 + 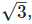 find the value of
find the value of 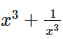
Solution: Given, x = 2 + 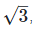 To find the value of
To find the value of 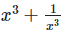
We have, x = 2 + 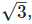
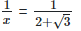
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 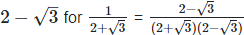
Since, (a + b) (
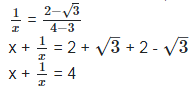
We know that, 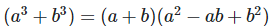
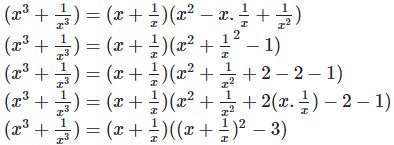
Putting the value of 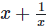 in the above equation, we get,
in the above equation, we get,
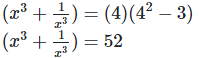
8. If x = 3 + 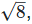 find the value of
find the value of 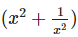
Solution: Given, x = 3 + 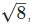
To find the value 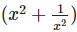 We have,
We have, 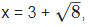
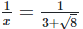
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
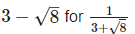
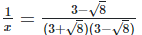
Since, (a + b) (a - b) = (a2−b2)
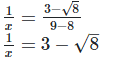
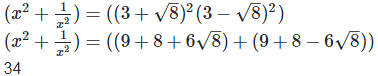
9. Find the value 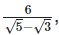
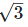 = 1.732 and
= 1.732 and 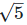 = 2.236.
= 2.236.
Solution. Given, 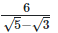 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 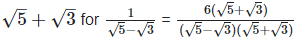
Since, (a + b) (a - b) = (a2−b2) = 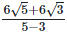
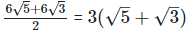 = 3(2.236+1.732) = 3(3.968) = 11.904
= 3(2.236+1.732) = 3(3.968) = 11.904
10. Find the values of each of the following correct to three places of decimals, it being given that 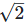 = 1.414,
= 1.414,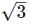 = 1.732,
= 1.732,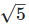 = 2.236,
= 2.236,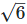 = 2.4495,
= 2.4495,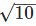 = 3.162
= 3.162
Solution. (i) 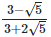 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 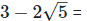
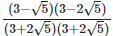
Since, (a + b) (a - b) = (a2−b2) =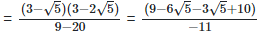
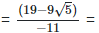
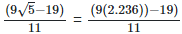
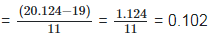
(ii) 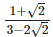 Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor
Rationalizing the denominator by multiplying both numerator and denominator with the rationalizing factor 
As we know, (a + b) (a - b) = (a2−b2) 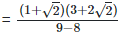
 = 7 + 7.07 = 14.07
= 7 + 7.07 = 14.07
11. If x = 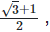 find the value of 4x3+2x2−8x+7.
find the value of 4x3+2x2−8x+7.
Solution: Given, 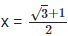
and given to find the value of 4x3+2x2−8x+7
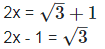
Now, squaring on both the sides, we get, (2x−1)2 = 3
4x2−4x+1 = 3
4x2−4x+1−3 = 0
4x2−4x−2 = 0
2x2−2x−1 = 0
Now taking 4x3+2x2−8x+7
2x(2x2−2x−1)+ 4x2+2x+2x2−8x+7
2x(2x2−2x−1)+ 6x2−6x+7
As, 2x2−2x−1=0
2x(0)+3(2x2−2x−1))+7+3
0+3(0)+10
10





















